一个基于广义Hamilton函数构造的新四维保守混沌系统

一个基于广义hamilton函数构造的新四维保守混沌系统
技术领域：
1.本发明涉及混沌信号生成和通信保密技术领域，尤其涉及利用规范方法对一个复杂的混沌信号生成系统的构造。


背景技术：

2.现今，耗散混沌系统已较为普遍，而保守混沌系统较为罕见，因为保守混沌系统与耗散混沌系统相比，其具有不存在奇异吸引子且不能被重构的独特优势。而将混沌信号应用在图像加密和视频加密中也是当今国内外研究的热点课题，利用混沌序列将原始图像和原始视频中像素点的位置进行置乱和像素点的大小进行改变，达到加密目的，保守系统因其独特性质在加密研究中具有比耗散混沌系统更深远的应用价值。目前保守混沌系统的设计和应用尚不成熟，很难达到实际应用的要求。因此，关于保守混沌系统和混沌信号的应用还需要进一步的研究工作。此外，由于早期的研究没有给出更具体可行的构造混沌系统方法，所以，混沌系统的构造方法在规范性上没有很大的突破。最近几年，有学者提出了一种利用广义hamilton函数构造混沌系统的方法，为构造混沌系统指明了一个新的方向，使混沌系统的构造具有了规范性。本发明中的系统是在广义hamilton函数的结构上构造的四维保守混沌系统，采用简单的系统结构便可以产生复杂的混沌信号。


技术实现要素：

3.本发明提供了基于广义hamilton函数构造的新四维保守混沌系统。该四维保守混沌系统能够产生复杂的混沌信号，可以有效地掩盖通信交流中的明文信息，达到良好的信息加密效果。
4.本发明为了实现发明目的，采用如下技术手段：
5.技术手段一：广义hamilton函数将系统分为保守项、耗散项和外力项三部分，本发明中的系统为保守系统，系统的结构矩阵如下：
[0006][0007]
通过构造保守项矩阵得到一个新的四维保守混沌系统，可以输出四路混沌信号，所述四维保守混沌系统对应的数学模型为：
[0008][0009]
式中，x1，x2，x3，x4分别为系统的状态变量；a，b为系统参数并全为实数。
[0010]
当a＝3，b＝6时，所述四维保守混沌系统存在混沌行为。
[0011]
技术手段二：一个四维保守混沌系统，其特征在于：
[0012]
所述一个新的四维保守混沌系统结构简单，只包含6项，其中包含4个非线性项和2个线性项，可调节参数只有a，b两个。基本的动力学特性包含对称性、耗散性、平衡点、特征值和稳定性。通常混沌系统中广泛存在着对称性，通过改变系统的变量验证系统所存在的对称性特点；耗散度是判断系统为保守系统或耗散系统的标准之一，耗散系统的耗散度小于零，而保守系统的耗散度等于零；平衡点是系统重要特征，通过特征值可以判断平衡点的类型，也可以通过特征值判定系统对应的平衡点的类别和稳定性。
[0013]
技术手段三：对技术手段二中所述的四维保守混沌系统进一步限定，其特征在于：
[0014]
该四维保守混沌系统，通过将(x1，-x2，-x3，-x4)代入系统的数学模型中，发现系统方程式发生改变，说明系统(2)不关于x1轴对称，再通过将(-x1，x2，-x3，-x4)，(-x1，-x2，x3，-x4)和(-x1，-x2，-x3，x4)分别代入系统的数学模型中，得出同样不关于x2轴和x4轴对称，该系统只关于x3轴对称，所以本系统具有对称性；通过公式说明该系统是体积保守的；当系统参数为a＝3，b＝6时，系统的lyapunov指数值分别为l1＝1.8162，l2＝0.0186≈0，l3＝-0.0182≈0，l4＝-1.8166。系统(2)只有一个平衡点s0＝(0，0，0，0)，其对应的特征值为两个零值和一对纯虚根λ1＝0，λ2＝0，λ3＝3i，λ4＝-3i，所以平衡点s0是中心点；根据混沌判定条件当系统中存在一个lyapunov指数值大于零就是混沌状态，所以在该组参数值下系统为混沌状态；另外本系统lyapunov指数值之和为零，即l1+l2+l3+l4＝0，所以，所以系统(2)为保守系统。
[0015]
本发明解决上述技术问题的技术手段是通过对广义hamilton函数的研究，首先广义无耗散hamilton函数可表示如下：
[0016][0017]
这里x∈r
n
是系统(3)的状态变量；u∈r
m
×1为系统(3)的输入，可看作系统(3)受到的广义力；g(x)∈r
n
×
m
为输入矩阵；为系统(3)的输出，可以看作系统的广义速度；j(x)∈r
n
×
n
是反对称矩阵，满足j(x)＝-j
t
(x)，常被称为结构阵，表示系统的能量保守部分；是关于状态变量x的hamilton函数，即能量存储函数。其次，通过对对称阵的构造得到混沌系统中状态变量的线性和非线性耦合项，最后通过多次实验来确定混沌系统的参数和初值。
附图说明：
[0018]
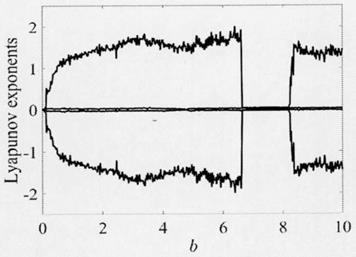
图1是系统(2)在初始条件为(5，2，-4，7)条件下的lyapunov指数图。
[0019]
图2是系统(2)在x
1-x2截面上x3＝0处的poincar
é
截面图。
[0020]
图3是系统(2)中状态变量x1与状态变量x2的二维相图。
[0021]
图4是系统(2)中状态变量x1与状态变量x3的二维相图。
[0022]
图5是系统(2)中状态变量x1与状态变量x4的二维相图。
[0023]
图6是系统(2)中状态变量x2与状态变量x3的二维相图。
[0024]
图7是系统(2)中状态变量x2与状态变量x4的二维相图。
[0025]
图8是系统(2)中状态变量x3与状态变量x4的二维相图。
具体实施方式：
[0026]
下面结合附图对本发明做详细描述。
[0027]
实施方式一：广义hamilton函数将系统分为保守项、耗散项和外力项三部分，本发明中的系统为保守系统，系统的结构矩阵如下：
[0028][0029]
通过构造保守项矩阵得到一个新的四维保守混沌系统，所述四维保守混沌系统可以输出四路混沌信号，其特征在于：
[0030]
1.所述新的四维保守混沌系统对应的数学模型为：
[0031][0032]
式中，x1，x2，x3，x4分别为系统状态变量；a，b为系统参数且全为实数。
[0033]
当a＝3，b＝6时，所述四维保守混沌系统存在混沌吸引子，任意两个系统状态变量的二维相图参见图3至图8。
[0034]
2.一个新的四维保守混沌系统，其特征在于：
[0035]
所述四维保守混沌系统包含6项，其中包含4个非线性项和2个线性项，可调节参数只有a，b两个。基本的动力学特性包含对称性、耗散性、平衡点、特征值和稳定性。通常混沌系统中广泛存在对称性，通过改变系统的变量验证系统所存在的对称性特点；耗散度是判断系统为保守系统或耗散系统的标准，耗散系统的耗散度小于零，而保守系统的耗散度等于零；平衡点是系统重要特征，通过特征值可以判断平衡点的类型，也可以通过特征值判定系统对应的平衡点的类别和稳定性。
[0036]
3.对所述的一个新的四维保守混沌系统进一步限定，其特征在于：
[0037]
该四维保守混沌系统，通过将(x1，-x2，-x3，-x4)代入系统的数学模型中，发现系统方程式发生改变，说明系统(2)不关于x1轴对称，再通过将(-x1，x2，-x3，-x4)，(-x1，-x2，x3，-x4)和(-x1，-x2，-x3，x4)分别代入系统的数学模型中，得出同样不关于x2轴和x4轴对称，该系统只关于x3轴对称，所以本系统具有对称性；通过公式说明该系统是体积保守的；当系统参数为a＝3，b＝6时，系统的lyapunov指数值分别为l1＝1.8162，l2＝0.0186≈0，l3＝-0.0182≈0，l4＝-1.8166。系统(2)只有一个平衡点s0＝(0，0，0，0)，这是该系统的一个显著特点。在平衡点s0＝(0，0，0，0)处进行线性化，得系统jacobi矩阵为：
[0038]
[0039]
4.根据det(j(s0)-λi)＝0，解得系统特征值为λ1＝0，λ2＝0，λ3＝3i，λ4＝-3i，所得到的平衡点为中心点；根据混沌判定条件当系统中存在一个lyapunov指数大于零就是混沌状态，所以本系统为混沌状态；另外本系统lyapunov指数之和为零，即l1+l2+l3+l4＝0，所以，所述系统为保守混沌系统。