智能反射面辅助的多用户MIMO上行能效谱效联合优化方法与流程

本发明属于通信领域，具体涉及一种利用部分信道状态信息的智能反射面辅助的多用户mimo上行能效谱效联合优化方法。

背景技术：

智能反射面(intelligentreflectingsurface，irs)是由一种由被动无源的反射单元组成的可编程表面，通过控制反射元件的形状、大小和方向等，每一个反射单元能够独立地改变入射信号的相位或幅度。

在irs辅助的无线通信系统中，在发送端和接收端之间加入irs，信号由发送端发出经irs反射到达接收端。irs的每个元件独立地对入射信号进行相位或幅度的改变，因此能够智能地重新配置无线传播环境，从而显著提高无线通信网络的性能。

在irs辅助的多用户mimo上行通信中，为了更好地平衡系统的能效和谱效，需要联合设计各用户上行发送信号的功率分配矩阵和irs的反射系数最大化能效和谱效的加权和。传统的无线传输方法设计通常基于瞬时信道状态信息，但是在高移动性等场景下，瞬时信道状态信息获取困难，因此本发明给出了一种基于部分信道状态信息的irs辅助的多用户mimo上行传输方法。对于最大化能效谱效加权和的优化问题，由于目标函数是非凸的且irs反射系数的约束也是非凸的，求解通常较为困难。此外，目标函数需要求期望，当irs反射单元数量较多时，计算复杂度很高。

技术实现要素：

发明目的：针对irs辅助的多用户mimo上行链路传输，本发明提供一种利用部分信道状态信息的能效谱效联合优化的irs辅助多用户mimo上行链路传输方法，能够有效提高系统的能效和谱效，实现能效和谱效的平衡，并降低实现复杂度。

技术方案：为实现上述发明目的，本发明所述的能效谱效联合优化的irs辅助的多用户mimo上行链路传输方法，包括以下步骤：

在多用户mimo上行传输中，各用户发送信号到达智能反射面irs，irs的每个反射单元能够独立地改变入射信号的相位，经irs反射后的信号到达基站；各用户最优发送信号协方差矩阵的特征向量，即各用户上行发送信号的方向，可由各用户到irs的信道矩阵的发送相关阵的特征向量确定；中央控制器利用部分信道状态信息，包括各用户到irs的统计信道状态信息和irs到基站的瞬时信道状态信息，以能效谱效联合优化为准则联合设计各用户的功率分配矩阵和irs的反射系数；所述联合优化问题的目标为在满足各用户发送功率约束和irs各反射系数的约束下最大化系统能效和谱效的加权和，其中谱效为系统遍历和速率，能效为系统带宽与谱效的乘积，再与系统总功率消耗的比值；

其中各用户的功率分配矩阵和irs反射系数的联合优化基于如下交替优化方法：在给定irs反射系数的条件下，利用确定性等同原理和quadratic变换，迭代优化得到局部最优的功率分配矩阵；在给定各用户功率分配矩阵的条件下，利用块坐标下降法、二次惩罚方法、minorization-maximization(mm)方法和加速投影梯度下降法设计irs的反射系数；迭代、交替实施各用户功率分配矩阵和irs端反射系数的优化过程直至相邻两次能效和谱效的加权和之差小于某个给定的阈值；

随着通信过程中各用户和irs之间的统计信道状态信息以及irs和基站之间的瞬时信道状态信息发生变化，中央控制器更新部分信道状态信息，动态实施能效谱效联合优化的多用户mimo上行发送功率分配和irs反射系数调整。

作为优选，所述对于给定的irs反射系数，利用确定性等同原理和quadratic变换，迭代优化得到局部最优的功率分配矩阵，包括以下步骤：

(1)根据大维随机矩阵理论，利用部分信道状态信息计算系统谱效、即系统遍历和速率的确定性等同值，进而计算目标函数的确定性等同值；

(2)能效谱效联合优化的功率分配问题是一个分式规划问题，目标函数是一个分子为凹函数分母为线性函数的分式函数与一个凹函数的和，利用quadratic变换，引入辅助变量将该优化问题转换为一系列凹优化子问题迭代求解，此辅助变量随着迭代过程不断更新；迭代过程在相邻两次目标函数之差小于某个给定阈值时终止，此时得到给定irs反射系数的条件下，各用户上行发送功率分配矩阵的局部最优解。

作为优选，所述对于给定的各用户功率分配矩阵，利用块坐标下降法、二次惩罚方法、mm方法和加速投影梯度下降法设计irs的反射系数，包括以下步骤：

(1)固定确定性等同辅助变量并将其视作常数；忽略优化问题中与反射系数无关的，可视为常数的项，得到简化的优化问题；引入两个辅助变量，将优化问题转化为等效的均方误差mse最小化问题；

(2)通过块坐标下降法迭代优化mse最小化问题中的各个变量，包括irs的反射系数和两个引入的辅助变量，步骤包括：

(21)固定irs反射系数和其中一个辅助变量，根据闭式解更新另一个辅助变量；

(22)固定irs反射系数和步骤(21)中已更新的辅助变量，根据闭式解更新另一个辅助变量；

(23)固定两个已更新的辅助变量，利用二次惩罚方法、mm方法和加速投影梯度下降法优化irs反射系数；

(24)迭代上述过程，直至前后两次目标函数之差小于某个给定阈值时终止，此时得到给定各用户上行功率分配矩阵的条件下，irs反射系数的一个优化解；

(3)根据优化后的irs反射系数更新确定性等同辅助变量；

(4)迭代上述过程，直至前后两次目标函数之差小于某个给定阈值时终止。

作为优选，所述系统遍历频谱效率表示为：

其中，为irs到基站的信道矩阵，m为基站接收天线数，nr为irs反射单元数，为第k个用户到irs的信道矩阵，u2,k和v2,k是确定性酉矩阵，分别表示接收和发送相关阵的特征矩阵，nk为第k个用户的发送天线数，φ＝diag{φ1,...,φnr}为对角矩阵，第n个对角线元素φn为irs的第n个反射单元的反射系数，为各用户功率分配矩阵的集合，λk为第k个用户的发送功率分配矩阵，k为小区中用户总数，im表示一个m×m的单位矩阵，σ²表示噪声方差，log表示对数运算，det表示取矩阵的行列式运算，e{.}表示期望运算。

作为优选，所述系统能效表示为：

其中，ξk(＞1)为第k个用户功率放大器效率的倒数，pc,k为第k个用户处的静态电路功耗，pbs和nrps分别为基站和irs的静态硬件耗散功率，tr{·}表示取矩阵迹的运算。

作为优选，所述系统能效和谱效的联合优化问题表示为：

s.t.tr{λk}≤pmax,k,

λk≥0,k＝1,...,k,

其中，

β＞0为加权系数，pmax,k为第k个用户的最大发送功率约束，为irs反射系数的约束，当irs反射系数的相位可以连续取值时，其中是虚数单位，θ是irs的反射系数的相位；当irs反射系数的相位只能取有限个离散值时，τ是可取的离散相位值的个数。

作为优选，在块坐标下降法中，固定两个引入的辅助变量，利用二次惩罚方法、mm方法和加速投影梯度下降法优化irs反射系数的迭代方法包括：

(1)在块坐标下降法中，将引入的两个辅助变量看作常数求解irs的反射系数时，反射系数的约束是非凸约束，利用二次惩罚方法引入一个惩罚因子，给目标函数加上一个二次惩罚项，将原问题转换为一个凸约束问题；

(2)转换后的凸约束问题的目标函数是非凸函数，利用mm方法将这个非凸的优化问题转换为一系列凸优化子问题迭代求解，在每一次迭代过程中，利用上一次迭代得到的irs反射系数的解构造一个原目标函数的上界函数，这个上界函数是凸函数，得到的凸优化子问题用加速投影梯度方法求解，迭代过程在相邻两次迭代的目标函数之差小于某个给定阈值时终止。

有益效果：与现有技术相比，本发明具有如下优点：

1.利用irs辅助多用户mimo上行传输，在发送端和接收端之间加入irs，irs的每个反射元件能够独立地改变入射信号的相位或幅度，因此能够智能地重新配置无线传播环境，从而显著提高无线通信网络的性能。

2.本发明只需利用部分信道状态信息，包括快时变的用户到irs信道的统计信道状态信息和慢时变的irs到基站的瞬时信道状态信息，降低了信道状态信息获取的复杂度和开销。中央控制器根据部分信道状态信息，对各用户的上行发送功率分配矩阵和irs的反射系数进行联合设计，从而提高系统的能效和谱效，实现能效和谱效的有效平衡。

3.利用确定性等同原理、quadratic变换，块坐标下降法、二次惩罚方法、mm方法和加速投影梯度下降等方法，联合设计各用户的发送协方差矩阵和irs的反射系数，最大化能效和谱效的加权和，有效平衡系统的能效和谱效。本发明提出的方法能够显著降低优化问题求解和物理层实现的复杂度。

附图说明

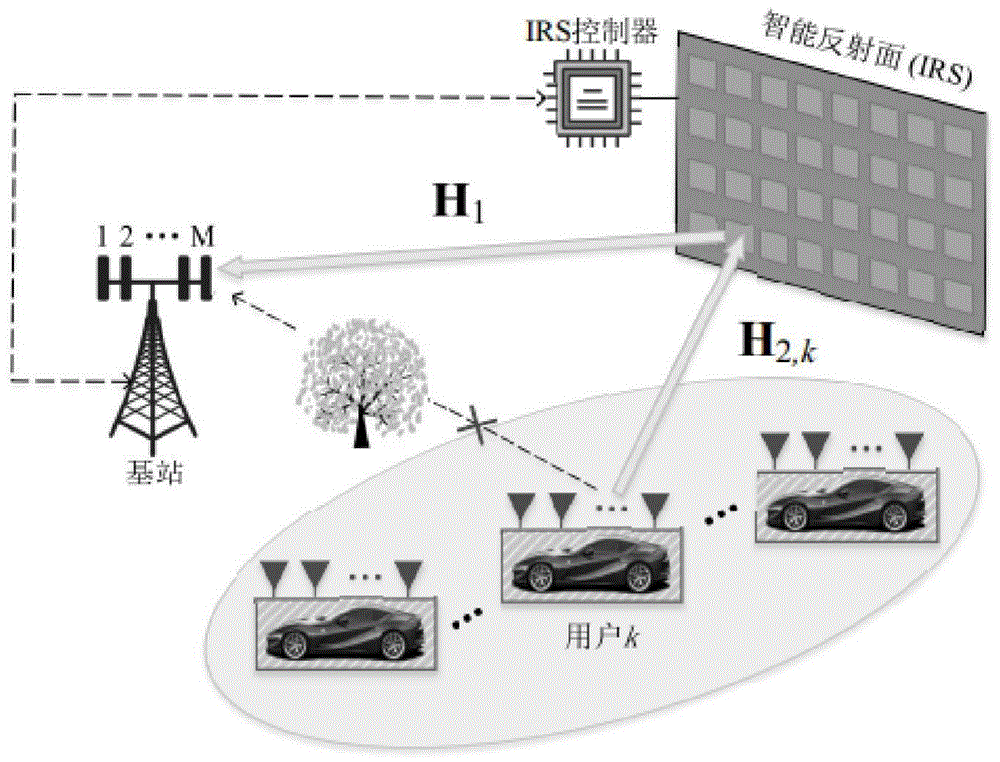
图1为本发明实施例中的irs辅助的多用户mimo上行传输示意图。

图2为本发明实施例中基于交替优化方法的能效谱效联合优化算法流程图。

图3为本发明实施例中基于quadratic变换的算法流程图。

图4为本发明实施例中的基于确定性等同原理的算法流程图。

图5为本发明实施例中的基于块坐标下降法的迭代算法流程图。

图6为本发明实施例中的基于二次惩罚方法、mm方法和加速投影梯度下降法的算法流程图。

具体实施方式

为了使本技术领域的人员更好地理解本发明方案，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整的描述，显然，所描述的实施例仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都应当属于本发明保护的范围。

本发明实施例公开的智能反射面辅助的多用户mimo上行能效谱效联合优化方法中，各个用户端发送信号，信号经irs反射到达基站，irs的每个反射单元能够独立地对入射信号进行相位调整。首先，利用各用户到irs的信道矩阵的发送相关阵的特征向量，可确定各用户最优发送信号协方差矩阵的特征向量，即各用户上行发送信号的方向。进一步的，中央控制器利用部分信道状态信息，包括各用户到irs的统计信道状态信息和irs到基站的瞬时信道状态信息，以能效谱效联合优化为准则联合设计各用户的上行发送功率分配矩阵和irs的反射系数。所述联合优化问题的目标为在满足各用户发送功率约束和irs各反射系数的约束下最大化系统能效和谱效的加权和，其中谱效为系统遍历和速率，能效为系统带宽与谱效的乘积，再与系统总功率消耗的比值。

其中各用户的上行发送功率分配矩阵和irs反射系数的联合优化基于如下交替优化方法：在给定irs反射系数的条件下，利用确定性等同原理和quadratic变换，迭代优化得到局部最优的功率分配矩阵；在给定各用户功率分配矩阵的条件下，利用块坐标下降法、二次惩罚方法、minorization-maximization(mm)方法和加速投影梯度下降法设计irs的反射系数；迭代、交替实施上述各用户端功率分配矩阵和irs端反射系数的优化过程直至相邻两次目标函数值之差、即能效和谱效的加权和之差小于某个给定的阈值。

随着通信过程中各用户和irs之间的统计信道状态信息以及irs和基站之间的瞬时信道状态信息发生变化，中央控制器更新部分信道状态信息，动态实施能效谱效联合优化的多用户mimo上行发送功率分配和irs反射系数调整。

其中，所述在给定irs反射系数的条件下，利用确定性等同原理和quadratic变换，迭代优化得到局部最优的功率分配矩阵，包括：

(1)根据大维随机矩阵理论，利用部分信道状态信息计算系统谱效、即系统遍历和速率的确定性等同值，进而计算目标函数的确定性等同值；

(2)能效谱效联合优化的功率分配问题是一个分式规划问题，目标函数是一个分子为凹函数分母为线性函数的分式函数与一个凹函数的和，利用quadratic变换，引入辅助变量将该优化问题转换为一系列凹优化子问题迭代求解，此辅助变量随着迭代过程不断更新；迭代过程在相邻两次目标函数之差小于某个给定阈值时终止，此时得到给定irs反射系数的条件下，各用户上行发送功率分配矩阵的局部最优解。

所述在给定各用户功率分配矩阵的条件下，利用块坐标下降法、二次惩罚方法、mm方法和加速投影梯度下降法设计irs的反射系数，包括：

(1)固定确定性等同辅助变量并将其视作常数；忽略优化问题中与反射系数无关的，可视为常数的项，得到简化的优化问题；引入两个辅助变量，将优化问题转化为等效的均方误差mse最小化问题；

(2)通过块坐标下降法迭代优化mse最小化问题中的各个变量，包括irs的反射系数和两个引入的辅助变量，步骤包括；

(21)固定irs反射系数和其中一个辅助变量，根据闭式解更新另一个辅助变量；

(22)固定irs反射系数和步骤(21)中已更新的辅助变量，根据闭式解更新另一个辅助变量；

(23)固定两个已更新的辅助变量，利用二次惩罚方法、mm方法和加速投影梯度下降法优化irs反射系数；

(24)迭代上述过程，直至前后两次目标函数之差小于某个给定阈值时终止，此时得到给定各用户上行功率分配矩阵的条件下，irs反射系数的一个优化解；

(3)根据优化后的irs反射系数更新确定性等同辅助变量；

(4)迭代上述过程，直至前后两次目标函数之差小于某个给定阈值时终止。

具体地，基于确定性等同的方法包括：

(a)依据大维随机矩阵理论，通过用户到irs信道的统计信道状态信息以及irs到基站信道的瞬时信道状态信息，迭代确定性等同辅助变量直至收敛；

(b)利用迭代得到的确定性等同辅助变量计算联合优化目标ρre的确定性等同值；

(c)将目标函数的确定性等同值带入能效谱效的联合优化问题中，避免高复杂度的求期望运算，降低运算的复杂度。

在块坐标下降法中，固定两个引入的辅助变量，利用二次惩罚方法、mm方法和加速投影梯度下降法优化irs反射系数的迭代方法包括：

(a)在块坐标下降法中，将引入的两个辅助变量看作常数求解irs的反射系数时，对于反射系数的约束是非凸约束，利用二次惩罚方法引入一个惩罚因子，给目标函数加上一个二次惩罚项，将原问题转换为一个凸约束问题；

(b)转换后的凸约束问题的目标函数是非凸函数，利用mm方法将这个非凸的优化问题转换为一系列凸优化子问题迭代求解，在每一次迭代过程中，利用上一次迭代得到的irs反射系数的解构造一个原目标函数的上界函数，这个上界函数是凸函数，得到的凸优化子问题用加速投影梯度方法求解，迭代过程在相邻两次迭代的目标函数之差小于某个给定阈值时终止。

下面结合具体场景对本发明实施例的具体步骤进行说明：

1)irs辅助的多用户mimo上行传输场景

考虑irs辅助的多用户mimo上行传输场景，基站配置m根天线，小区中有k个用户，每个用户配置nk根天线，在基站和用户中间有一个irs，irs配置nr个反射单元，每个反射单元能够独立地改变入射信号的相位。为对角矩阵，第n个对角线元素φn为irs的第n个反射单元的反射系数。为irs到基站的信道矩阵，m为基站接收天线数，nr为irs反射单元数，为第k个用户到irs的信道矩阵，根据联合相关瑞利衰落信道模型，h2,k可以分解为其中u2,k和v2,k是确定性酉矩阵，分别表示接收和发送相关阵的特征矩阵，为第k个用户到irs的统计特征模式域信道矩阵，表示h2,k的统计信道状态信息，其中运算符⊙表示矩阵的hadamard乘积，e{.}表示期望运算，(.)^*表示矩阵的共轭运算。

系统的谱效可以表示为：

其中，为各用户发送信号协方差矩阵的集合，qk为第k个用户的发送信号的协方差矩阵，σ²表示噪声方差，log表示对数运算，det表示取矩阵的行列式，im表示一个m×m的单位矩阵，(.)^h表示矩阵的共轭转置运算。

系统的能效定义为系统带宽与谱效的乘积，再与系统总功率消耗的比值，即

其中，w为系统带宽，ξk(＞1)为第k个用户功率放大器效率的倒数，tr{qk}为第k个用户的发送功率，pc,k为第k个用户处的静态电路功耗，pbs和nrps分别为基站和irs的静态硬件耗散功率，tr{·}表示取矩阵迹的运算。联合优化问题的目标函数定义为能效和谱效的加权和，即：

其中β＞0是一个常数，表示加权因子，能够控制能效和谱效的平衡与折中，pmax,k为第k个用户的最大发送功率约束。在irs辅助的多用户mimo上行传输过程中，为了同时提高系统能效和谱效，实现两者的有效平衡，需要对发送信号的协方差矩阵qk(k＝1,…,k)和irs的反射系数矩阵φ进行联合优化。上述irs辅助的多用户mimo上行传输系统中能效谱效联合优化的问题可以表示为：

其中，为irs反射系数的约束，当irs反射系数的相位可以连续取值时，其中是虚数单位，θ是irs的反射系数的相位；当irs反射系数的相位只能取有限个离散值时，τ是可取的离散相位值的个数。对各用户的发送协方差矩阵进行特征值分解，即其中vq,k是qk的特征矩阵，由qk的特征向量构成，代表第k个用户发送信号的方向，λk是对角矩阵，对角线元素是qk的特征值，表示第k个用户的发送功率分配矩阵。各用户最优发送信号协方差矩阵的特征向量可由各用户到irs的信道矩阵的发送相关阵的特征向量确定，也即由此，可将联合设计各用户发送信号协方差矩阵和irs反射系数的优化问题简化为联合设计各用户发送功率分配矩阵和irs反射系数的优化问题，即：

其中，为各用户发送功率分配矩阵的集合，

此问题目标函数非凸，很难得到全局最优解，且目标函数带有期望运算，计算复杂度很高。为此，本发明提出了一种利用部分信道状态信息的能效谱效联合优化的irs辅助多用户mimo上行传输方法，该方法包括了基于交替优化的迭代算法、基于确定性等同的迭代算法、基于quadratic变换的迭代算法、基于块坐标下降法的迭代算法，和基于二次惩罚方法、mm方法和加速投影梯度下降法的迭代算法。下面结合上述优化问题模型对涉及的各个算法做详细说明。

2)算法一：基于交替优化的最大化能效谱效加权和的迭代算法

基于交替优化方法原理，迭代、交替地优化用户的功率分配矩阵λ和irs的反射系数矩阵φ，直到目标函数收敛。图2示出了基于交替优化的最大化能效谱效加权和的迭代算法流程图，算法的详细过程如下：

步骤1：选取合适的初值λ⁽⁰⁾,φ⁽⁰⁾，设置迭代次数指示t＝0，阈值ε1；

步骤2：固定φ^(t)并将其代入算法二中，利用算法二优化各用户的功率分配矩阵，得到的结果记为λ^(t+1)；

步骤3：固定λ^(t+1)并将其代入算法四中，利用算法四优化irs的反射系数矩阵，得到的结果记为φ^(t+1)；

步骤4：根据步骤3和步骤4得到的解λ^(t+1)和φ^(t+1)计算新的目标函数值ρre(λ^(t+1),φ^(t+1))。将第t+1次迭代得到的结果ρre(λ^(t+1),φ^(t+1))与第t次迭代得到的结果ρre(λ^(t),φ^(t))进行比较，如果两次的差|ρre(λ^(t+1),φ^(t+1))-ρre(λ^(t),φ^(t))|小于阈值ε1，则终止迭代；否则，将迭代次数t加1，即t＝t+1，回到步骤2，重复上述步骤。

在通信过程中，随着各用户和irs之间的统计信道状态信息以及irs和基站之间的瞬时信道状态信息发生变化，中央控制器根据更新后的部分信道状态信息重复前述步骤，进行irs辅助的多用户mimo能效谱效联合优化的上行传输设计，从而实现传输过程的动态更新，以保障传输性能。

3)算法二：基于确定性等同原理和quadratic变换的迭代算法

基于交替优化方法的原理，在算法一的步骤2中，需要在给定irs反射系数矩阵φ的条件下，优化各用户的上行发送功率分配矩阵λ。上述固定φ，关于λ的优化问题表述如下：

其中，

在计算目标函数中系统谱效的表达式时，需要对用户到irs的瞬时信道进行遍历，计算期望值。由于该期望没有闭式表达式，因而需要monte-carlo仿真计算。为了降低求期望运算的复杂度，本发明利用大维矩阵随机理论计算目标函数的确定性等同表达。确定性等同方法利用用户到irs信道的统计信道状态信息，通过迭代计算确定性等同辅助变量，即可获得目标函数值的逼近结果。将问题(8)的目标函数替换为其确定性等同表达，并求解如下问题：

其中，和分别为系统谱效和能效的确定性等同表达，可由算法三计算得到。

上述问题中，由于目标函数非凸，通常很难直接获得最优的发送功率分配矩阵。具体的，是关于λ的凹函数，p(λ)是关于λ的线性函数(也是凸函数)，因此目标函数是一个凹函数加上一个凹-凸分式函数的形式，可以利用quadratic变换，通过迭代求解一系列凹优化子问题等效求解问题(12)。本算法进一步采用quadratic变换迭代计算出能效谱效联合优化的功率分配结果。图3示出了基于确定性等同原理和quadratic变换的迭代算法流程图，算法的详细过程如下：

步骤1：给定irs反射系数矩阵φ，初始化各用户的发送功率分配矩阵λ⁽⁰⁾，设置迭代次数指示q＝0，阈值ε2；

步骤2：利用算法三，根据λ^(q)计算目标函数的确定性等同表达值

步骤3：根据quadratic变换原理，求解如下凹优化问题：

其中y^(q+1)是引入的辅助变量，由第q次的迭代结果λ^(q)计算

步骤4：利用算法三，根据λ^(q+1)计算新的目标函数的确定性等同表达值将第q+1次迭代得到的结果与第q次迭代得到的结果进行比较，如果两次的差小于给定的阈值ε2，则终止迭代；否则，将迭代次数q加1，即q＝q+1，回到步骤3，重复上述步骤。

4)算法三：基于确定性等同原理的迭代算法

系统谱效的确定性等同表达为：

其中，当确定性等同辅助变量和已知时，γk和πk可由下列式子计算得到：

其中确定性等同辅助变量γ和ψ可通过迭代求解下式等式确定：

其中是的第m列，λk,n,n和gk,n,n分别是λk和γk的第(n,n)个元素。图4示出了基于确定性等同原理的迭代算法流程图，算法的详细过程如下：

步骤1：对于每一个用户k，初始化确定性等同辅助变量和设置迭代次数指示u＝0，阈值ε3；

步骤2：利用根据式(18)更新得到

步骤3：利用根据式(19)更新得到

步骤4：将第u+1次迭代得到的辅助变量的值与第u次迭代得到的结果进行比较，如果两次的差小于给定的阈值ε3，则终止迭代，转到步骤5；否则，将迭代次数u加1，即u＝u+1，回到步骤2，重复上述步骤。

步骤5：利用步骤4中得到的确定性辅助变量和根据式(16)和式(17)计算γk和πk，k＝1,...,k，进而根据式(15)计算系统谱效的确定性等同值

步骤6：利用步骤5得到的谱效的确定性等同值计算：

5)算法四：基于块坐标下降法的迭代算法

基于交替优化方法的原则，在算法一的步骤3中，需要在给定各用户上行发送功率分配矩阵λ的条件下，优化irs的反射系数矩阵φ。当λ固定时，系统的总功耗p(λ)确定，是一个与φ无关的常数，因此最大化系统能效和谱效的加权和等效于最大化系统的谱效，即上述固定λ，关于φ的优化问题可以简化为：

确定性等同辅助变量(γ,ψ)和φ的优化采取交替优化的方式，即先固定(γ,ψ)，优化φ；然后根据算法三中式(18)和式(19)更新(γ,ψ)。当(γ,ψ)固定时，它们可以被看作是与φ无关的常数，则问题(22)的目标函数表达式中只有第二项与φ相关，其余项可看作关于φ的常数，在优化时可以忽略，从而将问题(22)简化为：

引入辅助wc,uc变量，将问题(23)转换为一个等效的最小化均方误差的优化问题，表述如下：

其中，

对于问题(24)中需要求解的三个变量wc，uc和φ，当其中两个变量固定时，目标函数是关于另一个变量的凹函数。因此，可基于块坐标下降法，交替优化求解这三个变量。图5示出了基于块坐标下降法的迭代算法流程图，算法的详细过程如下：

步骤1：初始化wc⁽⁰⁾,uc⁽⁰⁾,φ⁽⁰⁾，设置迭代次数指示s＝0，阈值ε4。计算问题(24)中的目标函数值f5a(wc^(s),uc^(s),φ^(s))；

步骤2：利用uc^(s)和φ^(s)根据式(25)计算ec，则固定uc^(s)和φ^(s)时，wc的解可以表示为：

步骤3：固定wc^(s+1)和φ^(s)，uc的解可以表示为：

步骤4：固定wc^(s+1)和uc^(s+1)，利用算法五优化φ得到的解记为φ^(s+1)；

步骤5：根据wc^(s+1)，uc^(s+1)和φ^(s+1)计算新的目标函数值f5a(wc^(s+1),uc^(s+1),φ^(s+1))，将第s+1次迭代得到的结果与第s次迭代得到的结果进行比较，如果两次的差|f5a(wc^(s+1),uc^(s+1),φ^(s+1))-f5a(wc^(s),uc^(s),φ^(s))小于给定的阈值ε4，则终止迭代；否则，将迭代次数s加1，即s＝s+1，回到步骤2，重复上述步骤。

6)算法五：基于二次惩罚方法、mm方法和加速投影梯度下降法的迭代算法

在算法四的步骤4中，需要固定wc和uc优化φ。当wc和uc固定时，忽略与φ无关的常数项，则对于φ的优化可以表述为如下问题：

其中，因为φ是对角矩阵，所以优化φ只需要优化它的对角线元素。定义利用对角矩阵的性质，上述问题(29)可以等效为以下优化φ的问题：

其中，表示复数的实部。上述问题(30)的约束是非凸的，可以利用二次惩罚方法将其转换为一个等效的凸约束问题，表述如下：

其中，λ＞0表示惩罚因子，||·||表示向量的二范数，表示集合的凸包，对于它的凸包为对于其凸包是一个以为顶点的正多边形。定义集合则问题(31)的目标函数fλ(φ)在集合上利普希茨连续，l是其利普希茨常数。当惩罚因子λ＞λ时，问题(30)和问题(31)是等效的。对于对于

问题(31)的目标函数是非凸函数，可以利用mm方法将其转换为一系列凸优化问题迭代求解。在每一次迭代过程中，利用上一次迭代得到的irs反射系数的解构造一个原目标函数的上界函数。在第l次迭代过程中需要求解的子问题表述为：

其中，表示两个复向量内积的实部。问题(32)是一个平滑的凸优化问题，可以利用加速投影梯度下降法求解：

z^(l)＝φ^(l)+α(l)(φ^(l)-φ^(l))，(34)

其中，表示φ在上的投影，表示的梯度，表示步长。初始化ζ(-1)＝0，则α(l)由以下式子计算得到：

此外，在式(33)中的步长需要满足以下不等式：

图6示出了基于二次惩罚方法、mm方法和加速投影梯度下降法的迭代算法流程图，算法的详细过程如下：

步骤1：给定整数常数j≥1，c≥1，外插序列{α(l)}l≥0，初始的惩罚因子λ＞0以及惩罚因子的上界值λupp。初始化设置迭代次数指示l＝0，阈值ε5。

步骤2：计算z^(l)＝φ^(l)+α(l)(φ^(ll)-φ^(l-1))；

步骤3：利用回溯线搜索方法找到满足不等式(37)的步长

步骤4：计算

步骤5：将第l+1次迭代的结果与第l次迭代的结果进行比较，如果两次的差||φ^(l+1)-φ^(l)||小于给定的阈值ε5，则更新惩罚因子λ＝λc；

步骤6：将迭代次数l加1，即l＝l+1，回到步骤2，重复上述步骤；每重复j次，则更新惩罚因子λ＝λc，检查λ的大小，若λ≥λupp，终止迭代，得到φ＝diag{φ^(l+1)}；否则，回到步骤2，重复上述步骤。