一种基于Tent映射和复合混沌映射的图像加密方法与流程

本发明涉及图像加密技术领域，特别指一种基于tent映射和复合混沌映射的图像加密方法。

背景技术：

随着多媒体技术和互联网的飞速发展，越来越多的图像被传输、共享和存储在互联网上。而图像的信息安全一直是数字世界中的一个严重问题，虽然存在一些传统的加密算法具有较高的安全性和成熟的验证能力，例如des算法和rsa算法，但由于图像数据的特殊性，传统的加密算法并不适合图像加密领域。图像在空间域中通常用像素位置和像素值这两种信息来进行描述，所以图像加密算法主要围绕置乱和扩散两部分设计，由于混沌系统具有非周期性、不可预测性、伪随机性以及初值敏感性等优点，十分适合用于图像加密领域。

由于一维混沌映射存在映射分布不均匀的缺点，导致基于一维混沌映射的图像加密算法的加密效果不好，并且还存在密钥空间小的问题，使得算法不能抵抗暴力攻击；虽然高维混沌映射具有复杂的混沌行为并且难以预测，但是会导致算法具有很高的执行成本，对计算机的运算能力要求比较高。同时，一个好的图像加密方法还需要具有抵抗明文攻击的能力。

因此，如何提供一种基于tent映射和复合混沌映射的图像加密方法，实现提升图像加密的安全性，降低执行成本，成为一个亟待解决的问题。

技术实现要素：

本发明要解决的技术问题，在于提供一种基于tent映射和复合混沌映射的图像加密方法，实现提升图像加密的安全性，降低执行成本。

本发明是这样实现的：一种基于tent映射和复合混沌映射的图像加密方法，包括如下步骤：

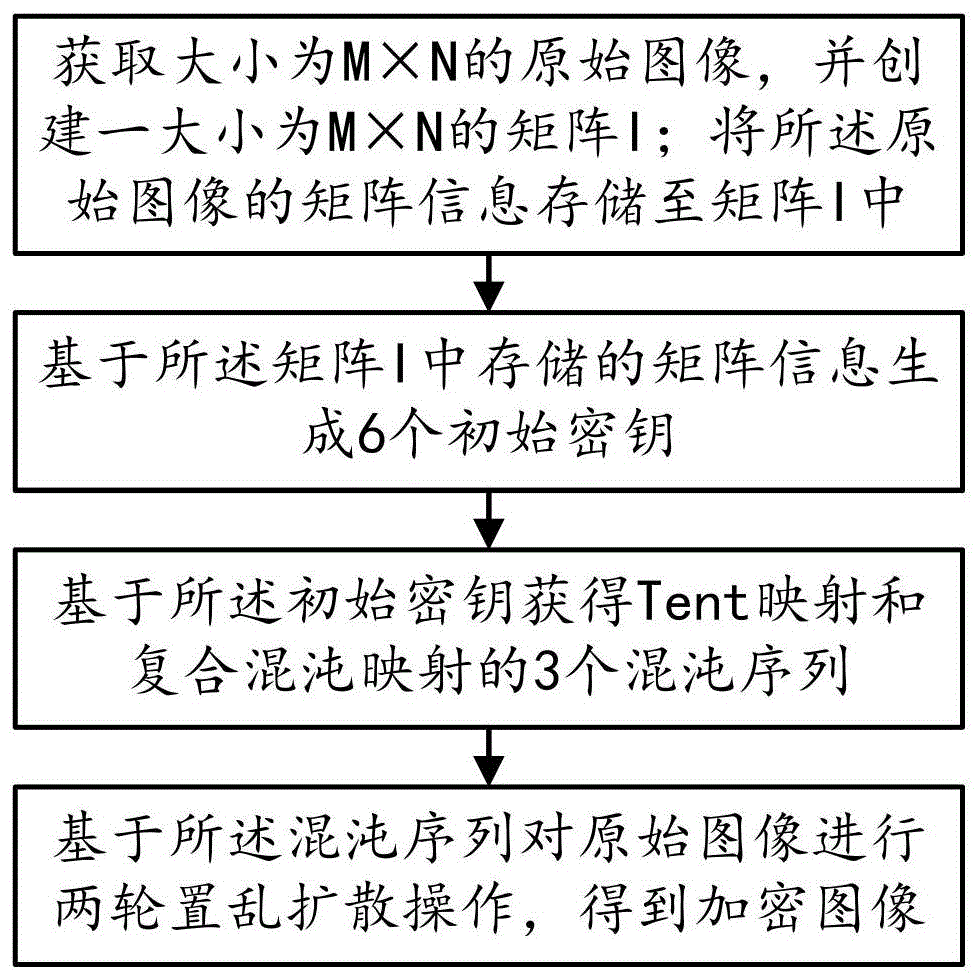
步骤s10、获取大小为m×n的原始图像，并创建一大小为m×n的矩阵i；将所述原始图像的矩阵信息存储至矩阵i中；

步骤s20、基于所述矩阵i中存储的矩阵信息生成6个初始密钥；

步骤s30、基于所述初始密钥获得tent映射和复合混沌映射的3个混沌序列；

步骤s40、基于所述混沌序列对原始图像进行两轮置乱扩散操作，得到加密图像。

进一步地，所述步骤s10中，所述矩阵信息包括像素位置以及像素值。

进一步地，所述步骤s20具体包括：

步骤s21、创建一个大小为1×4的一维矩阵x，随机生成3个取值范围在0至1的随机数并存储在所述一维矩阵x的前3列；求取所述矩阵信息中所有像素值的和并存储在一维矩阵x的第4列；

步骤s22、基于所述一维矩阵x计算复合混沌映射系数e1、e2、e3以及e4：

步骤s23、基于各所述复合混沌映射系数计算初始密钥x(1)、y(1)、a、μ、u以及z(1)：

x(1)＝e1；

y(1)＝e2；

a＝2+e3；

μ＝0.99+e4；

u＝1.999999+e4；

z(1)＝0.000001+e4。

进一步地，所述步骤s30具体为：

基于各所述初始密钥获得tent映射和复合混沌映射的混沌序列s1、s2以及s3，并将3个所述混沌序列映射到0至255范围内的伪随机序列rn：

rn＝mod(ceil(sn×10^3),256),n＝{1,2,3}。

进一步地，所述步骤s30中，所述tent映射的数学模型为：

其中u表示控制参数，且取值范围为[0，2]；zn为tent映射的迭代变量，且初始值z1的取值范围为(0，1)时，tent映射进入混沌区。

进一步地，所述步骤s30中，所述复合混沌映射是采用sine映射和chebyshev映射作为种子映射，利用扰动分叉参数生成的映射，所述复合混沌映射的数学模型为：

其中μ的取值范围为(0，1]；xn表示输出的混沌序列，取值范围为(0，1)；初始密钥a的绝对值不小于2时，复合混沌映射进入混沌区，在无限精度条件下产生无限长度非周期混沌实值序列；yn的取值范围为[-1，1]；c表示加权参数，取值为0.1；n表示迭代次数；μ1表示控制参数μ的迭代初值；a1表示控制参数a的迭代初值；xn+1、yn+1表示复合混沌映射的迭代变量；μn+1、an+1表示控制参数的迭代变量。

进一步地，所述步骤s40具体包括：

步骤s41、利用circshift函数对所述矩阵i进行第一轮置乱，得到图像i1；

步骤s42、利用复合混沌映射生成的伪随机序列r2对所述图像i1进行第一轮扩散，得到矩阵c：

其中i表示矩阵的位置信息；c(i)表示矩阵c中第i个数；c(i+1)表示矩阵c中第i+1个数；

步骤s43、利用tent映射生成的伪随机序列r3对所述矩阵c进行位异或操作，得到第二扩散乱生成的矩阵cc；

步骤s44、利用复合混沌映射生成的伪随机序列r1对所述矩阵cc进行洗牌打乱，得到第二轮置乱生成的加密图像ccc。

本发明的优点在于：

1、通过采用sine映射和chebyshev映射作为种子映射，利用扰动分叉参数生成复合混沌映射，提高了复合混沌映射的复杂度，有效的扩大了密钥空间，进而极大的提升了图像加密的安全性。

2、通过将两个一维混沌映射组成一个新的复合混沌映射，进而极大的降低了图像加密算法的执行成本，减轻了对计算机运算能力的依赖。

3、通过将明文矩阵信息中的像素值作为初始密钥的生成依据，极大的提高了图像加密算法抵抗明文攻击的能力。

附图说明

下面参照附图结合实施例对本发明作进一步的说明。

图1是本发明一种基于tent映射和复合混沌映射的图像加密方法的流程图。

图2是本发明一种基于tent映射和复合混沌映射的图像加密方法的流程示意图。

图3是本发明原始图像预处理示意图。

图4是本发明第二轮置乱示意图。

图5是本发明测试图像。

图6是本发明测试图像的加密效果图。

具体实施方式

请参照图1至图6所示，本发明一种基于tent映射和复合混沌映射的图像加密方法的较佳实施例之一，包括如下步骤：

步骤s10、获取大小为m×n的原始图像，并创建一大小为m×n的矩阵i；将所述原始图像的矩阵信息存储至矩阵i中；

步骤s20、基于所述矩阵i中存储的矩阵信息生成6个初始密钥；

步骤s30、基于所述初始密钥获得tent映射和复合混沌映射的3个混沌序列；去除各所述混沌序列的前1000个随机数，以保证所述混沌序列的随机性；

步骤s40、基于所述混沌序列对原始图像进行两轮置乱扩散操作，得到加密图像。

所述步骤s10中，所述矩阵信息包括像素位置以及像素值。

所述步骤s20具体包括：

步骤s21、创建一个大小为1×4的一维矩阵x，随机生成3个取值范围在0至1的随机数并存储在所述一维矩阵x的前3列；求取所述矩阵信息中所有像素值的和并存储在一维矩阵x的第4列；

步骤s22、基于所述一维矩阵x计算复合混沌映射系数e1、e2、e3以及e4：

步骤s23、基于各所述复合混沌映射系数计算初始密钥x(1)、y(1)、a、μ、u以及z(1)：

x(1)＝e1；

y(1)＝e2；

a＝2+e3；

μ＝0.99+e4；

u＝1.999999+e4；

z(1)＝0.000001+e4；

其中2、0.99、1.999999、0.000001为预设的初始值。

所述步骤s30具体为：

基于各所述初始密钥获得tent映射和复合混沌映射的混沌序列s1、s2以及s3，并将3个所述混沌序列映射到0至255范围内的伪随机序列rn：

rn＝mod(ceil(sn×10^3),256),n＝{1,2,3}；

所述伪随机序列rn包括利用复合混沌映射生成的伪随机序列r1、利用复合混沌映射生成的伪随机序列r2、利用tent映射生成的伪随机序列r3。

所述步骤s30中，所述tent映射的数学模型为：

其中u表示控制参数，且取值范围为[0，2]；zn为tent映射的迭代变量，且初始值z1的取值范围为(0，1)时，tent映射进入混沌区。

所述步骤s30中，所述复合混沌映射是采用sine映射和chebyshev映射作为种子映射，利用扰动分叉参数生成的映射，所述复合混沌映射的数学模型为：

其中μ的取值范围为(0，1]；xn表示输出的混沌序列，取值范围为(0，1)；初始密钥a的绝对值不小于2时，复合混沌映射进入混沌区，在无限精度条件下产生无限长度非周期混沌实值序列；yn的取值范围为[-1，1]；c表示加权参数，取值为0.1；n表示迭代次数；μ1表示控制参数μ的迭代初值；a1表示控制参数a的迭代初值；xn+1、yn+1表示复合混沌映射的迭代变量；μn+1、an+1表示控制参数的迭代变量。

所述步骤s40具体包括：

步骤s41、利用circshift函数对所述矩阵i进行第一轮置乱，得到图像i1；

步骤s42、利用复合混沌映射生成的伪随机序列r2对所述图像i1进行第一轮扩散，得到矩阵c：

其中i表示矩阵的位置信息；c(i)表示矩阵c中第i个数；c(i+1)表示矩阵c中第i+1个数；

步骤s43、利用tent映射生成的伪随机序列r3对所述矩阵c进行位异或操作，得到第二扩散乱生成的矩阵cc；

步骤s44、利用复合混沌映射生成的伪随机序列r1对所述矩阵cc进行洗牌打乱，得到第二轮置乱生成的加密图像ccc。

所述加密图像ccc的解密过程即图像加密算法的逆过程，解密和加密的初始密钥、混沌序列均相同。

本发明一种基于tent映射和复合混沌映射的图像加密方法的较佳实施例之二，包括如下步骤：

步骤s10、获取大小为512×512的测试图像(如图3所示)，并创建一大小为512×512的矩阵i；将所述原始图像的矩阵信息存储至矩阵i中；所述矩阵信息包括像素位置以及像素值；

步骤s20、基于所述矩阵i中存储的矩阵信息生成6个初始密钥；

步骤s30、基于所述初始密钥分别迭代tent映射和复合混沌映射(1000+512×512)次，生成3个混沌序列，并去除各所述混沌序列的前1000个随机数；

步骤s40、基于所述混沌序列对原始图像进行两轮置乱扩散操作，得到加密的测试图像(如图4所示)。

所述步骤s20具体包括：

步骤s21、创建一个大小为1×4的一维矩阵x，随机生成3个取值范围在0至1的随机数并存储在所述一维矩阵x的前3列；求取所述矩阵信息中所有像素值的和并存储在一维矩阵x的第4列；

步骤s22、基于所述一维矩阵x计算复合混沌映射系数e1、e2、e3以及e4：

步骤s23、基于各所述复合混沌映射系数计算初始密钥x(1)、y(1)、a、μ、u以及z(1)：

x(1)＝e1；

y(1)＝e2；

a＝2+e3；

μ＝0.99+e4；

u＝1.999999+e4；

z(1)＝0.000001+e4；

其中2、0.99、1.999999、0.000001为预设的初始值。

所述步骤s40具体包括：

步骤s41、利用circshift函数对所述矩阵i进行第一轮置乱，即将所述矩阵i看成一个一维矩阵，分别对所述矩阵i的每一行、每一列进行循环位移操作，进而得到图像i1；

步骤s42、利用复合混沌映射生成的伪随机序列r2对所述图像i1进行第一轮扩散，即将所述图像i1转换成一维行向量，图像i1和伪随机序列r2为大小相等的矩阵，分别取出i1和r2第一个位置的值相加后，对256进行mod操作，将mod操作的计算结果与前一个计算结果进行异或操作，以此类推，进而得到矩阵c：

其中i表示矩阵的位置信息；c(i)表示矩阵c中第i个数；c(i+1)表示矩阵c中第i+1个数；

步骤s43、利用tent映射生成的伪随机序列r3对所述矩阵c进行位异或操作，即将矩阵c和r3转换成大小为512×512的矩阵，对两个矩阵同时进行遍历，分别取出两个矩阵相同位置的值并转换成一个字符串形式表示的二进制数，然后进行二进制异或操作，再将结果转换成十进制，以此类推，进而得到第二扩散乱生成的矩阵cc；

步骤s44、利用复合混沌映射生成的伪随机序列r1对所述矩阵cc进行洗牌打乱，即对矩阵r1进行sort操作，将矩阵r1里的值进行升序排序，将矩阵r1的位置变化数据存储在一个新的位置矩阵中，根据位置矩阵对所述矩阵cc进行置乱，进而得到第二轮置乱生成的加密的测试图像。

综上所述，本发明的优点在于：

1、通过采用sine映射和chebyshev映射作为种子映射，利用扰动分叉参数生成复合混沌映射，提高了复合混沌映射的复杂度，有效的扩大了密钥空间，进而极大的提升了图像加密的安全性。

2、通过将两个一维混沌映射组成一个新的复合混沌映射，进而极大的降低了图像加密算法的执行成本，减轻了对计算机运算能力的依赖。

3、通过将明文矩阵信息中的像素值作为初始密钥的生成依据，极大的提高了图像加密算法抵抗明文攻击的能力。

虽然以上描述了本发明的具体实施方式，但是熟悉本技术领域的技术人员应当理解，我们所描述的具体的实施例只是说明性的，而不是用于对本发明的范围的限定，熟悉本领域的技术人员在依照本发明的精神所作的等效的修饰以及变化，都应当涵盖在本发明的权利要求所保护的范围内。