无线传感器低功耗低时延路径式协同计算方法

本发明属于通信领域，具体涉及一种无线传感器低功耗低时延路径式协同计算方法。

背景技术：

随着物联网技术的不断成熟以及5g无线网络的大规模建设，万物互联时代即将到来。而作为物联网底层网络的重要技术形式，无线传感器网络(wirelesssensornetwork,wsn)得到了快速而广泛的发展，目前已被成功应用到了包括军事、自然环境监测、医疗保健、智能家居、物流跟踪等在内的多个领域之中。

现有的wsn系统一般由传感器节点、汇聚(sink)节点、远程管理中心三部分组成。传感器节点一般集成有一个或多个不同类型的传感器，主要负责采集监测区域的信息，并将采集到的数据通过一跳或多跳传递到汇聚节点；汇聚节点是wsn的骨干节点，其主要功能是汇聚和转发网络报文，具有较强的数据处理能力和通信能力；远程管理中心相当于云平台，利用网络资源虚拟化技术构成资源池，存储和处理wsn发来的数据，并将处理过的数据发送给用户。然而，wsn采集的数据传到云计算中心进行计算产生的通信开销大，时延高，无法有效支撑如军事侦察等时延敏感型业务。

针对云计算模式存在的高传输时延问题，学者们提出了边缘计算技术，通过将数据分割并利用网络边缘设备(如wsn中的汇聚节点)的计算能力完成计算，缩短了数据的传播距离。但传统的边缘计算技术不适合处理端到端的业务，缺乏边传输边计算的能力。

针对传统边缘计算存在的问题，有学者提出了基于步骤可分割的路径式协同计算技术。该技术采用由多个服务功能组成的有向无环图(directedacyclicgraph,dag)模型表征业务，通过将dag形式的任务图映射到网络图，利用网络边缘设备的能力，在数据传输的过程中完成业务处理，实现业务的边传输边计算，更适合处理复杂的新型信息业务；而且每个网络节点只需加载映射到其上的服务功能即可，能有效降低单个网络设备的计算负载，适用于负载能力受限的wsn节点。

针对路径式协同计算技术的早期研究，学者们为优化网络的路径计算速率，将业务表示为树状图或有向无环图形式并将其映射到网络上。rost等学者在考虑了节点约束能力的同时，提出了将任务图的边与节点同时映射至网络拓扑图的方案，并在分布式云网络场景中求解了最佳任务调度方案。michael等制定了具有分支的任务图映射方案，将任务图扩展到任意dag模型。

但是上述关于路径式协同计算的研究均未考虑节点的能耗问题，wsn处理的任务增多导致网络整体能耗增加，缩短wsn节点的工作寿命，且wsn节点通常位于野外，能量受限并难以补充，因此，路径式协同计算如何进行任务映射，使得在能耗约束的前提下业务处理时延最短，成为一个急需解决的技术问题。

技术实现要素：

发明目的：针对云计算应用于无线传感器网络时延敏感型业务时存在的高传输时延问题，提出了一种无线传感器低功耗低时延路径式协同计算方法。该方法基于一种云雾网络架构，该架构利用汇聚节点组成雾计算层；在数据传输过程中基于雾计算层的计算能力分步骤完成任务计算,降低任务处理时延；由于汇聚节点计算能力较弱，时延降低将导致能耗增加，无线传感器系统工作寿命减短，为此提出能耗约束下的任务映射策略，并利用离散二进制粒子群优化(binaryparticleswarmoptimization,bpso)算法解决能耗约束下的时延优化问题。

技术方案：无线传感器低功耗低时延路径式协同计算方法，包括以下步骤：

(1)、构建wsn云雾网络架构；

(2)、制定能耗约束下的任务映射策略：

基于步骤(1)得到的wsn云雾网络架构，将dag形式的有向无环图g映射至无向连通图u的雾网络中，并构建有向无环图g至无向连通图u的最优映射关系模型；

(3)、利用bpso算法求解步骤(2)得到的最优映射关系模型。

进一步地，步骤(1)中的wsn云雾网络架构自下而上包括感知层、雾计算层、云计算层，其中：

所述感知层由集成有一个或多个类型传感器的无线传感器组成，用于对所在部署区域进行监测；

所述雾计算层由多个具备数据处理能力和通信能力的汇聚节点组成，所述汇聚节点与无线传感器通信互联，所述雾计算层用于转发和处理感知层产生的数据；

所述云计算层由多个服务器集群构成，服务器集群通过通信链路与汇聚节点通信互联相连，用于对wsn云雾网络架构进行监控和管理。

进一步地，步骤(2)包括以下步骤：

(21)、构建dag形式的有向无环图g至无向连通图u的映射规则模型：

在dag形式的有向无环图g至无向连通图u的映射规则模型中，有向无环图g＝(ω，γ)表示任务模型，定义ω＝{ω1,ω2,…,ωs,ωs+1,…,ωl-1,ωl|s≥1,l＞s+1}为g的节点集合，其中：

ω1,ω2,…,ωs是s个任务起点，ωs+1,…,ωl-1是中间任务节点，ωl是任务终点；

γ为g的有向边集合，定义φ↑(ωi)＝{ωj|(ωj,ωi)∈γ}为ωi的前向节点集合；

此外，wsn拓扑图用无向连通图u＝(v,k)来表示，定义v＝{ν1,ν2,…,νs,νs+1,…,νt-1,νt|s≥1,t＞s+1}为u的节点集合，其中ν1,ν2,…,νs指业务发起节点，νs+1,…,νt-1为中继节点，νt为与用户直连的节点；

k为u的边集合，每条边均支持双向数据传输，用来表示节点vi到vj的最短路径；

定义为最短路径集合；

为最短路径中所经过的数据转发节点集合；为从节点vi到vj沿最短路径传输单位数据量的时延；

将图u的网络边传输速率和节点连接关系作为输入，通过floyed算法可求得

有向无环图g至无向连通图u的映射规则如下：

定义1.ω至v的映射规则为ε:ω→v，且ε需满足式(1)条件：

ε将ω的任务起点ω1,ω2,…,ωs映射为v的任务发起节点ν1,ν2,…,νs；将中间任务节点ωs+1,…,ωl-1映射为任意中继节点νs+1,…,νt-1；将任务终点ωl映射为与用户直连的节点νt；

定义2.γ至p的映射为υ:γ→p，且υ需满足式(2)的条件：

υ将集合γ中的有向边映射为图u中的节点ε(ωi)至ε(ωj)的最短路径

(22)、基于步骤(21)得到的映射规则模型构建时延模型：

子任务ωi在某次映射关系中的时延可以表示为式(3)：

其中：

为进行到子任务ωi时的累积时延；

为ωi计算时延；

为节点ε(ωi)的计算能力；

α为任务计算复杂度系数；

则有向无环图g的任务处理时延为任务终点ωl的时延，如式(4)所示：

t(g)＝t(ωl)(4)

(23)、基于步骤(21)得到的映射规则模型、步骤(22)得到的时延模型构建能耗模型，其中：

网络节点vi的能耗等于网络节点vi的空闲能耗与活动能耗之和；

(231)、空闲能耗

(2311)映射节点ε(ωi)的空闲能耗如式(5)所示：

其中，指ε(ωi)空闲状态时的功率；

指ε(ωi)在某次任务中处于空闲状态的时间；

分别为计算时间、发送数据时间、接收数据时间，并且此三者无重合，其计算公式如式(6)-(8)所示：

由式(5)-(8)得ε(ωi)的空闲能耗如式(9)：

(2312)转发节点的空闲能耗如式(10)所示：

可利用式(11)-(12)计算：

由(10)-(12)得的空闲能耗如式(13)所示：

(232)、活动能耗：

活动能耗包括计算能耗和传输能耗：

(2321)、计算能耗：

计算能耗仅由映射节点ε(ωi)产生，如式(14)：

其中k＞0和σ≥2都是正实数，σ和k分别被设置为3和10^-28；

(2322)、传输能耗：

映射节点ε(ωi)的传输能耗如式(15)-(16)：

其中，pt和pr分别为节点的发送功率和接收功率，因此ε(ωi)的活动能耗如式(17)：

转发节点的活动能耗仅包括传输能耗，如式(18)：

由式(9)、(17)得，映射节点ε(ωi)的总能耗如式(19)：

由式(13)、(18)得，转发节点的总能耗如式(20)：

整个雾网络的总能耗如式(21)所示：

令整个雾网络所含有的最大能量为e^max，则在某次任务g内，网络所产生的能耗需小于等于其最大能耗，如式(22)：

(24)、构建dag形式的有向无环图g至无向连通图u映射规则优化模型——基于步骤(21)-步骤(23)给出dag形式的有向无环图g至无向连通图u的映射规则，优化模型，建立二值优化问题：

定义3.子任务节点ωp和雾网络节点vq的映射关系如下：当时，即为ωp映射为vq；当时，ωp不会映射为vq，则满足式(23)：

基于定义3，ωp至vq的映射可以构建为l×t的映射矩阵x，如式(24)：

则式(5)所表示的子任务ωi的时延可表示为式(25)：

任务g的时延可以表示为x的函数，如式(26)：

t(g)＝f(x)(26)

式(19)所表示的映射节点ε(ωi)的总能耗可表示为式(27)：

式(20)所表示的转发节点的总能耗可表示为式(28)：

则能耗约束下有向无环图g至无向连通图u的最优映射关系建模如下：

x＝argmin(f(x))

进一步地，步骤(3)中bpso算法主要用于优化离散空间的约束问题，将粒子的位置限制为0或1，适用于式(29)所提出的二值优化问题：

采用bpso算法时，粒子群在搜索空间i内移动寻找最好位置，中nmax为迭代次数最大值，m为粒子群规模，n∈{1,2,…,nmax}为迭代次数；

在第n次迭代中，第i个粒子的位置和速度可分别表示为：

式(30)中，xⁿ(i)∈i，

式(31)中，vⁿ(i)∈o，

第i个粒子在第n次迭代中，速度更新公式如式(32)：

式(32)中，和分别为粒子局部和全局最优位置，w为惯性权重，γ1和γ2为加速因子，β1和β2为在区间[0,1]内均匀分布的随机数；

bpso算法的位置更新公式如式(33)-(34)：

本算法的适应度函数如式(35)：

f(x)＝t(g)＝f(x)(35)。

有益效果：本发明公开的无线传感器低功耗低时延路径式协同计算方法具有以下有益效果：

1、基于云雾网络架构，将路径式协同计算技术引入wsn，利用wsn中的汇聚节点构成雾计算层，将dag形式的时延敏感型业务映射到汇聚节点上，利用其计算能力进行分步骤计算，实现业务的边传输边计算，降低了业务处理时延；

2、考虑到wsn节点能耗有限，业务必须在一定的能耗约束下完成，因此将能耗约束考虑进路径式协同计算技术内。

附图说明

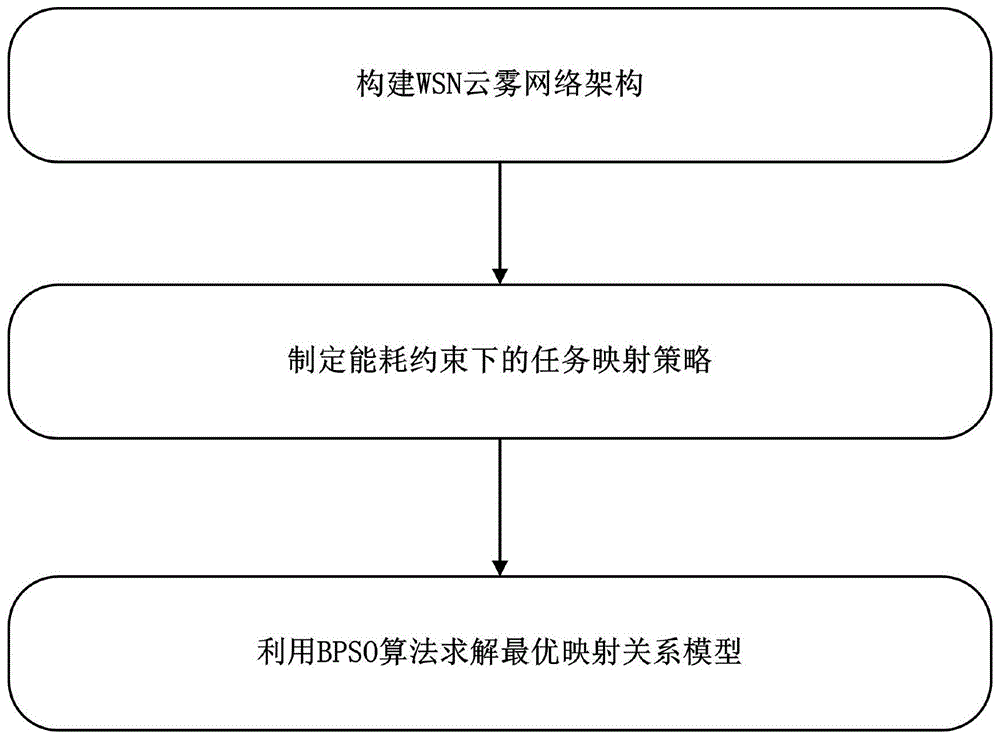
图1为本发明公开的无线传感器低功耗低时延路径式协同计算方法的流程图。

图2为wsn云雾网络架构的示意图。

图3为有向无环图g至无向连通图u映射的示意图，其中：

1-云计算层

11-通信链路

2-雾计算层

21-汇聚节点

22-用户

3-感知层

31-无线传感器

32-部署区域

具体实施方式：

下面对本发明的具体实施方式详细说明。

如图1所示，无线传感器低功耗低时延路径式协同计算方法，包括以下步骤：

(1)、构建wsn云雾网络架构；

(2)、制定能耗约束下的任务映射策略：

基于步骤(1)得到的wsn云雾网络架构，将dag形式的有向无环图g映射至无向连通图u的雾网络中，并构建有向无环图g至无向连通图u的最优映射关系模型；

(3)、利用bpso算法求解步骤(2)得到的最优映射关系模型。

进一步地，如图2所示，步骤(1)中的wsn云雾网络架构自下而上包括感知层3、雾计算层2、云计算层1，其中：

所述感知层3由集成有一个或多个类型传感器的无线传感器31组成，用于对所在部署区域32进行监测；

所述雾计算层2由多个具备数据处理能力和通信能力的汇聚节点21组成，所述汇聚节点21与无线传感器通信互联，所述雾计算层2用于转发和处理感知层3中用户22产生的数据；

所述云计算层1由多个服务器集群构成，服务器集群通过通信链路11与汇聚节点21通信互联相连，用于对wsn云雾网络架构进行监控和管理。

进一步地，步骤(2)包括以下步骤：

(21)、构建dag形式的有向无环图g至无向连通图u的映射规则模型：

在dag形式的有向无环图g至无向连通图u的映射规则模型中，有向无环图g＝(ω，γ)表示任务模型，定义ω＝{ω1,ω2,…,ωs,ωs+1,…,ωl-1,ωl|s≥1,l＞s+1}为g的节点集合，其中：

ω1,ω2,…,ωs是s个任务起点，ωs+1,…,ωl-1是中间任务节点，ωl是任务终点；

γ为g的有向边集合，定义φ↑(ωi)＝{ωj|(ωj,ωi)∈γ}为ωi的前向节点集合；

此外，wsn拓扑图用无向连通图u＝(v,k)来表示，定义v＝{ν1,ν2,…,νs,νs+1,…,νt-1,νt|s≥1,t＞s+1}为u的节点集合，其中ν1,ν2,…,νs指业务发起节点，νs+1,…,νt-1为中继节点，νt为与用户直连的节点；

k为u的边集合，每条边均支持双向数据传输，用来表示节点vi到vj的最短路径；

定义为最短路径集合；

为最短路径中所经过的数据转发节点集合；

为从节点vi到vj沿最短路径传输单位数据量的时延；

将图u的网络边传输速率和节点连接关系作为输入，通过floyed算法可求得

有向无环图g至无向连通图u的映射规则如下：

定义1.ω至v的映射规则为ε:ω→v，且ε需满足式(1)条件：

ε将ω的任务起点ω1,ω2,…,ωs映射为v的任务发起节点ν1,ν2,…,νs；将中间任务节点ωs+1,…,ωl-1映射为任意中继节点νs+1,…,νt-1；将任务终点ωl映射为与用户直连的节点νt；

定义2.γ至p的映射为υ:γ→p，且υ需满足式(2)的条件：

υ将集合γ中的有向边映射为图u中的节点ε(ωi)至ε(ωj)的最短路径

(22)、基于步骤(21)得到的映射规则模型构建时延模型：

子任务ωi在某次映射关系中的时延可以表示为式(3)：

其中：

为进行到子任务ωi时的累积时延；

为ωi计算时延；

为节点ε(ωi)的计算能力；

α为任务计算复杂度系数；

则有向无环图g的任务处理时延为任务终点ωl的时延，如式(4)所示：

t(g)＝t(ωl)(4)

(23)、基于步骤(21)得到的映射规则模型、步骤(22)得到的时延模型构建能耗模型，其中：

网络节点vi的能耗等于网络节点vi的空闲能耗与活动能耗之和；

(231)、空闲能耗

(2311)映射节点ε(ωi)的空闲能耗如式(5)所示：

其中，指ε(ωi)空闲状态时的功率；

指ε(ωi)在某次任务中处于空闲状态的时间；

分别为计算时间、发送数据时间、接收数据时间，并且此三者无重合，其计算公式如式(6)-(8)所示：

由式(5)-(8)得ε(ωi)的空闲能耗如式(9)：

(2312)转发节点的空闲能耗如式(10)所示：

可利用式(11)-(12)计算：

由(10)-(12)得的空闲能耗如式(13)所示：

(232)、活动能耗：

活动能耗包括计算能耗和传输能耗：

(2321)、计算能耗：

计算能耗仅由映射节点ε(ωi)产生，如式(14)：

其中k＞0和σ≥2都是正实数，σ和k分别被设置为3和10^-28；

(2322)、传输能耗：

映射节点ε(ωi)的传输能耗如式(15)-(16)：

其中，pt和pr分别为节点的发送功率和接收功率，因此ε(ωi)的活动能耗如式(17)：

转发节点的活动能耗仅包括传输能耗，如式(18)：

由式(9)、(17)得，映射节点ε(ωi)的总能耗如式(19)：

由式(13)、(18)得，转发节点的总能耗如式(20)：

整个雾网络的总能耗如式(21)所示：

令整个雾网络所含有的最大能量为e^max，则在某次任务g内，网络所产生的能耗需小于等于其最大能耗，如式(22)：

(24)、构建dag形式的有向无环图g至无向连通图u映射规则优化模型——基于步骤(21)-步骤(23)给出dag形式的有向无环图g至无向连通图u的映射规则，优化模型，建立二值优化问题：

定义3.子任务节点ωp和雾网络节点vq的映射关系如下：当时，即为ωp映射为vq；当时，ωp不会映射为vq，则满足式(23)：

基于定义3，ωp至vq的映射可以构建为l×t的映射矩阵x，如式(24)：

则式(5)所表示的子任务ωi的时延可表示为式(25)：

任务g的时延可以表示为x的函数，如式(26)：

t(g)＝f(x)(26)

式(19)所表示的映射节点ε(ωi)的总能耗可表示为式(27)：

式(20)所表示的转发节点的总能耗可表示为式(28)：

则能耗约束下有向无环图g至无向连通图u的最优映射关系建模如下：

进一步地，步骤(3)中bpso算法主要用于优化离散空间的约束问题，将粒子的位置限制为0或1，适用于式(29)所提出的二值优化问题：

采用bpso算法时，粒子群在搜索空间i内移动寻找最好位置，中nmax为迭代次数最大值，m为粒子群规模，n∈{1,2,…,nmax}为迭代次数；

在第n次迭代中，第i个粒子的位置和速度可分别表示为：

式(30)中，xⁿ(i)∈i，

式(31)中，vⁿ(i)∈o，

第i个粒子在第n次迭代中，速度更新公式如式(32)：

式(32)中，和分别为粒子局部和全局最优位置，w为惯性权重，γ1和γ2为加速因子，β1和β2为在区间[0,1]内均匀分布的随机数；

bpso算法的位置更新公式如式(33)-(34)：

本算法的适应度函数如式(35)：

f(x)＝t(g)＝f(x)(35)。

具体的bpso算法如下文所示：

上面对本发明的实施方式做了详细说明。但是本发明并不限于上述实施方式，在所属技术领域普通技术人员所具备的知识范围内，还可以在不脱离本发明宗旨的前提下做出各种变化。