基于相位加权共轭对称的滤波器组多载波定时同步方法

1.本发明属于通信技术领域，特别涉及一种定时同步方法，可用于滤波器组多载波fbmc系统。


背景技术：

2.滤波器组多载波fbmc通信系统是在ofdm的基础上发展出来的。正交频分复用ofdm是多载波调制技术的一种，也是第四代移动通信的核心技术之一。然而ofdm有两个缺陷：一个是ofdm系统为了消除多径干扰引入了循环前缀，增加了开销；另一个是对于没有波形成型的系统，ofdm系统在频域的旁瓣衰减缓慢，这导致了系统的频谱泄露较大。fbmc系统取消了循环前缀，因而提高了频谱利用率，另外，该系统中引入了原型滤波器组，使得其频谱旁瓣泄露问题得到了抑制。
3.无论是ofdm系统还是fbmc系统，用于确定数据符号的起始位置均采用定时同步模块实现，其算法的性能好坏直接影响到接收端能否正确解调出原始数据。现有的定时同步算法大致可以分为非数据辅助型同步和数据辅助型同步两类，其中：
4.非数据辅助型同步算法，无需添加训练符号进行辅助估计，而是仅仅依靠信号本身的结构和调制方法进行定时，性能表现较差，在实际通信场景下所能发挥的作用有限。
5.数据辅助型同步算法，需在发送信号中添加一定的训练符号，用于在接收端对定时进行辅助估计，尽管该方法增加了一定的开销，但其技术优势明显，且适用在实时性要求高的场景。
6.由于fbmc系统没有循环前缀，对时偏敏感，因而，在出现定时同步上的偏差时，会有符号间干扰，导致系统无法解调出数据。为了获得优良的系统性能，fbmc系统一般采用数据辅助型同步算法，以在接收端利用滑动窗口技术和自相关技术来获得定时同步位置。现有fbmc系统的定时同步算法可以借鉴ofdm系统的相关算法的思想，比如使用ofdm系统中的s&c算法和minn算法，也有学者提出了针对fbmc系统的定时同步算法，如修正的最小方差mls算法，及tonello和rossi提出的tr1、tr2算法。这几种算法虽然都可以实现定时同步功能，但是却都有各自的问题：s&c算法的定时测度曲线会有“峰值平台”现象出现；minn算法的定时测度曲线会有多峰现象；tr1、tr2和mls算法，由于是时频联合估计算法，其同步结构设计存在一定缺陷，使得其测度曲线没有尖锐的峰值出现，而是一条缓和变化的曲线。
7.上述这些现有方法的问题都将造成同步的准确率低，导致无法解调出原始数据。


技术实现要素：

8.本发明的目的在于针对上述现有技术存在的问题，提出一种基于相位加权共轭对称结构的滤波器组多载波定时同步方法，以提高定时同步的准确率。
9.本发明的技术方案是：在发送端，通过构造一种相位加权共轭对称的训练序列，并添加数据信号，组成发送信号；信号经过awgn信道之后，在接收端，通过对接收信号进行检测，利用门限粗略估计有效信号的起始位置，并利用定时测度函数确定数据的准确位置。其
实现步骤包括如下：
10.(1)在滤波器组多载波fbmc系统的发送端随机生成一段长度为n
d
的数据帧，并将其依次进行16阶oqam调制、ifft、多相网络滤波，得到有效信息数据s
d
(n)；
11.(2)构建相位加权的共轭对称的训练序列p
t
(m)和发送信号s(n)：
12.(2a)将长度为n
p
的zc序列，重复偶数k次，组成总长度为m＝kn
p
的训练序列，将该训练序列的前半段保持不变，后半段进行共轭逆序处理，得到共轭对称的训练序列：p(m)＝p
*
(m
‑1‑
m)，其中m＝0,1,2,...,m
‑
1，*表示共轭；
13.(2b)将另一个长度为m＝kn
p
的zc序列，打乱次序随机排列作为权重序列w(m)，并将其与p(m)对应相乘，生成相位加权的共轭对称的训练序列：p
t
(m)＝p(m)w(m)，m＝0,1,...,m
‑
1；
14.(2c)将相位加权的共轭对称的训练序列p
t
(m)添加在有效信息数据s
d
(n)之前，组成发送端的发送信号s(n)；
15.(3)将发送信号s(n)送入加性高斯白噪声awgn信道，在接收端得到接收信号r(n)；
16.(4)对接收信号r(n)进行粗同步检测：
17.(4a)设定起始位置d＝1；
18.(4b)对接收信号r(n)，从d位置开始取m个样点，得到取样序列r(d+m)，并将其与相位加权的共轭对称的训练序列p
t
(m)进行相关计算，得到相关值corr(d)和平均相关值corr
t
(d)：
19.(4c)将平均相关值corr
t
(d)与判决门限值t＝3.5进行比较：若corr
t
(d)≥t，则停止检测，执行(5)；否则，设d＝d+1，返回(4b)；
20.(5)对接收信号r(n)进行精细检测：
21.(5a)计算接收信号r(n)的测度函数值，并利用一个计数器计数，设置计数器初始数值为slider
c
＝0；
22.(5b)从d位置开始对r(n)取m个样点，得到取样序列r(d+m)，并利用权重序列w(m)对其进行权重释放，得到权重释放后的取样序列：r'(d+m)＝r(d+m)w
*
(m)；
23.(5c)将权重释放后的取样序列r'(d+m)进行重新排序，即将其前半段保持不变，对后半段进行共轭并逆序排列，得到重新排序后的取样序列r”(d+m)，并利用如下公式计算接收信号r(n)的测度函数值c(d)：
[0024][0025]
其中：
[0026]
(5d)更新计数器数值slider
c
＝slider
c
+1，并检查计数器数值slider
c
是否达到1024：若达到，则执行(6)；否则，设d＝d+1，返回(5b)；
[0027]
(6)将测度函数值c(d)最大时对应的d判定为最佳定时位置
[0028][0029]
本发明与现有技术相比具有以下优点：
[0030]
第一：由于本发明中采用了相位加权的共轭对称结构的训练序列，使得接收端在
精细检测时，只有在正确位置才能保证取样序列每个样点的权重被“释放”，并保证取样序列的前半段和后半段对应点相同，使得测度函数表现为一条尖锐的曲线，极大提高了定时的准确率；并通过对取样序列重新排序，使得其对应样点之间保持固定的相偏，具有抗频偏性能。
[0031]
第二：由于本发明中对接收序列首先利用门限进行粗同步检测，减小了精细检测范围，同时也避免出现精细检测范围比噪声序列短的现象。
附图说明
[0032]
图1是本发明使用的fbmc系统场景图；
[0033]
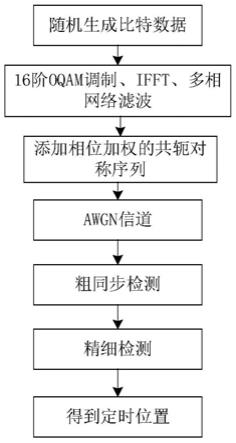
图2本发明的实现流程图；
[0034]
图3本发明中的16qam调制映射图；
[0035]
图4本发明中所用的帧结构图；
[0036]
图5是用本发明和现有tr1算法对定时准确率的仿真对比图；
[0037]
图6本发明在有无频偏情况下对定时准确率的仿真对比图；
[0038]
图7本发明和现有tr1算法对测度函数的仿真对比图。
具体实施方式
[0039]
下面结合附图对本发明实施和效果做进一步的描述。
[0040]
参照图1，本实例的应用场景是滤波器组多载波fbmc系统，该系统包括发送端和接收端，信道采用的是加性高斯白噪声awgn信道。发送端将二进制的数据帧依次进行16阶oqam调制，ifft，多相网络滤波，得到有效数据信号；利用一种具有相位加权的共轭对称结构的训练序列，与有效数据信号结合得到发送信号；在接收端，对接收信号进行粗同步检测和精细检测，得到定时测度函数最大值时对应的位置即为定时位置。
[0041]
参照图2，本实例的具体实现步骤如下：
[0042]
步骤1，生成有效数据信号。
[0043]
(1.1)在发送端随机生成数据帧为长度n
d
的二进制比特数据块d；
[0044]
(1.2)对数据块d进行fbmc多载波映射，得到有效数据信号s
d
(n)：
[0045]
(1.2.1)对数据块进行16阶oqam调制：
[0046]
将每4个比特，组成一个四位二进制数据，并将其低两位作为同相分量，高两位作为正交分量，按照图3所示规则，进行16qam调制；
[0047]
用每个映射结果的实部a
c
和虚部b
c
，交错组成一个新的oqam符号序列d
c
＝{d
c,0
,d
c,1
}，其中d
c,0
＝a
c
，d
c,1
＝b
c
，c表示第c个子载波，c＝0,1,...,w
‑
1，w表示子载波数量；
[0048]
将oqam符号d
c,0
乘以旋转因子d
c,1
乘以旋转因子得到最终调制数据其中j为虚数单位；
[0049]
(1.2.2)对调制数据a
w
进行ifft变换，得到映射数据x(i)：
[0050]
[0051]
其中，i＝0,1,2,...,w
‑
1；
[0052]
(1.2.3)对映射数据x
l
(i)采用多相网络滤波处理，得到第l个符号s
l
(n)：
[0053][0054]
其中，滤波器h
i
(n)为：
[0055][0056]
其中，原型滤波器h(n)为:
[0057][0058]
式中α为重叠因子，取值为4；滤波器各项系数如下：
[0059]
h1＝0.971960,h3＝0.235147；
[0060]
(1.2.4)由每个符号s
l
(n)得到有效信息数据s
d
(n)：
[0061][0062]
步骤2，构建相位加权的共轭对称的训练序列p
t
(m)和发送信号s(n)。
[0063]
(2.1)将长度为n
p
的zc序列，重复偶数k次，组成总长度为m＝kn
p
训练序列，将该训练序列的前半段保持不变，后半段进行共轭逆序处理，得到共轭对称的训练序列：p(m)＝p
*
(m
‑1‑
m)，其中m＝0,1,2,...,m
‑
1，*表示共轭；
[0064]
(2.2)将另一个长度为m＝kn
p
的zc序列，进行随机排列；随机排列的原理为：首先随机生成一个长度为m的服从(0，1)均匀分布的序列x(m)，将x(m)按从大到小排序之后，返回排序后的元素位于原序列x(m)中的索引位置；然后将该zc序列中的数据按照此索引位置重新排列，得到权重序列w(m)；
[0065]
(2.3)将p(m)和w(m)对应相乘，得到相位加权的共轭对称的训练序列：p
t
(m)＝p(m)w(m)，m＝0,...,m
‑
1；
[0066]
(2.4)将p
t
(m)添加在有效信号数据s
d
(n)之前，组成发送信号s(n)＝[p
t
(m),s
d
(n)]，该信号s(n)的结构如图4所示。
[0067]
步骤3，将发送信号s(n)送入加性高斯白噪声awgn信道，在接收端得到接收信号r(n)。
[0068]
步骤4，对接收信号r(n)进行粗同步检测。
[0069]
(4.1)设定起始位置d＝1；
[0070]
(4.2)对接收信号r(n)，从d位置开始取m个样点，得到取样序列r(d+m)，并将其与相位加权的共轭对称的训练序列p
t
(m)进行相关计算，得到相关值corr(d)和平均相关值corr
t
(d)，计算公式如下：
[0071]
[0072][0073]
其中，p
t
(m)为相位加权的共轭对称的训练序列，r
*
(d+m)表示对取样序列r(d+m)进行共轭运算；corr(t)表示t位置的相关值；
[0074]
(4.3)将平均相关值corr
t
(d)与判决门限值t＝3.5进行比较：若corr
t
(d)≥t，则停止检测，执行步骤5；否则，设d＝d+1，返回(4.2)；
[0075]
步骤5，对接收信号r(n)进行精细检测。
[0076]
(5.1)计算接收信号r(n)的测度函数值，并利用一个计数器计数，设置计数器初始数值为slider
c
＝0；
[0077]
(5.2)从d位置开始对r(n)取m个样点，得到取样序列r(d+m)，并利用权重序列w(m)对其进行权重释放，得到权重释放后的取样序列：r'(d+m)＝r(d+m)w
*
(m)；
[0078]
(5.3)将权重释放后的取样序列r'(d+m)进行重新排序，即将其前半段保持不变，对后半段进行共轭并逆序排列，得到重新排序后的取样序列r”(d+m)：
[0079][0080]
其中，r(d+m)表示取样序列的前半段，w(m)表示权重序列的前半段；表示取样序列的后半段，表示权重序列的后半段；
[0081]
(5.4)利用如下公式计算接收信号r(n)的测度函数值c(d)：
[0082][0083]
其中：
[0084]
(5.5)更新计数器数值slider
c
＝slider
c
+1，并检查计数器数值slider
c
是否达到1024：若达到，则执行步骤6；否则，设d＝d+1，返回(5.2)。
[0085]
步骤6，将测度函数值c(d)最大时对应的d判定为最佳定时位置
[0086][0087]
本发明的效果可以通过以下仿真进一步说明：
[0088]
一.仿真系统参数设置
[0089]
使用matlab r2018b仿真软件，设定fbmc系统子载波数量为512；p1(m)分四段，即k＝4，n
p
＝512，总长度为m＝2048。初始定时时刻位置d＝1，判决门限值t＝3.5。每个信噪比下仿真次数为1000次。
[0090]
二.仿真内容
[0091]
仿真1，在信噪比为[
‑
15db，
‑
10db，
‑
5db，0db]的情况下，对本发明和现有tr1同步
算法的定时准确率进行仿真，结果如图5。
[0092]
从图5结果可知，本发明相对现有tr1算法而言，定时准确率有极大的提升，本发明在
‑
5db时的定时准确率就能达到100％了；而现有tr1算法，由于测度函数曲线的不尖锐，极大的降低了其定时准确率。
[0093]
仿真2，在信噪比为[
‑
15db，
‑
10db，
‑
5db，0db]的情况下，对本发明中发送信号不加入频偏与加入频偏，两种情况下的定时准确率进行仿真，其中频偏为相对子载波间隔归一化值0.25，仿真结果如图6所示。
[0094]
从图6结果可知，加入频偏后对定时准确率的影响较小，在当前频偏下，仍然能在
‑
5db的情况下达到100％定时准确率，说明改进后的算法具有较好的抗频偏能力。
[0095]
仿真3，在信噪比为[
‑
5db，0db]的情况下，对本发明和现有tr1算法的定时测度函数进行仿真，结果如图7。其中：图7(a)是tr1算法在
‑
5db时的测度函数曲线；图7(b)是本发明在
‑
5db时的测度函数曲线；图7(c)是tr1算法在0db时的测度函数曲线；图7(d)是本发明在0db时的测度函数曲线。
[0096]
从图7可知，在同一个信噪比下，两种算法的测度函数曲线差别巨大，现有tr1算法的测度函数曲线没有尖锐的峰值出现，影响了定时位置的判定，而本发明出现了尖锐峰值，定时位置清晰可见。造成这种差别的原因在于两种算法的同步序列结构的不同，使得两种序列在错误时刻计算得到的相关值完全不同，在不考虑噪声和任何频偏的影响的情况下对两种算法进行对比分析，若最佳定时位置为d
c
，错误定时位置为d
e
＝d
c
+δd，分别对两种算法进行如下分析：
[0097]
对于现有tr1算法，在接收端的采样序列r(d+m)中，如果在正确位置定时，则有r(d
c
+m)＝r(d
c
+n
p
+m),m＝0,1,2,...,kn
p
‑
n
p
‑
1，可以计算出一个很大的相关值；然而在错误位置定时，仍然有r(d
e
+m)＝r(d
c
+δd+m)＝r(d
c
+δd+m+n
p
)＝r(d
e
+n
p
+m)，其中m＝
‑
δd,...,kn
p
‑
n
p
‑
δd
‑
1，这样也能得到一个较大的相关值，相关值的大小和定时偏差δd有关，最终表现为测度函数曲线为一条“和缓”变化的曲线。
[0098]
而本发明在正确位置定时由于或因而可计算得到一个很大的相关值；如果在错误位置，由于权重序列对齐错误和共轭对称中点选择错误，导致r”(d
e
+m)≠r”(d
e
+n
p
+m)，m＝0,...,kn
p
‑
n
p
‑
1，所以得到的相关值极小。最终表现为测度函数曲线出现了尖锐的峰值。
[0099]
由上分析可知，共轭对称结构能改善测度函数曲线，使其出现尖锐峰值，并最终提高定时准确率。