一种基于机器学习储备池计算的保密通信方法及系统

1.本发明涉及保密通信领域，尤其涉及一种基于机器学习储备池计算的保密通信方法及系统。


背景技术：

2.在保密通信研究领域，利用混沌系统进行加密一直是一个非常重要的方法。在传统混沌保密通信中，加密系统和解密系统往往需要是同一类系统，通过建立耦合，实现系统间混沌同步，从而进行解密。但是，同步解密系统在选择上不具备灵活性，一旦用于加密的混沌系统发生变化，也需要随之变化。此外，传统用于保密通信的混沌系统主要是非时滞的、有限维的，保密性不强。


技术实现要素：

3.发明目的：本发明提出一种保密性、灵活性强的保密通信方法。本发明的另一目的在于提供基于上述保密通信方法的系统。
4.技术方案：本发明所述的基于机器学习储备池计算的保密通信方法，包括步骤：
5.(1)发送端的时滞混沌系统生成的混沌信号u(t)，所述混沌信号u(t)包括训练集u1(t)和加密集u2(t)；
6.(2)利用所述加密集u2(t)对发送端发送的信号h(t)进行加密，生成加密信号s(t)；
7.(3)接收端接收训练集u1(t)，经过储备池计算前处理模块对信号进行归一化处理后得到信号向量v'(t)，输入到储备池计算模块中，所述储备池计算模块输出信号向量v(t)；
8.(4)发送端将加密集u2(t)中的某一个维度的标量信号发送给接收端，用于替代信号向量v(t)中同一维度的信号，将得到的信号再次输入到所述储备池计算前处理模块中更新v'(t)；
9.(5)对接收端接收的加密信号s(t)和所述储备池计算模块同步输出的信号向量v(t)进行解密，得到发送端发送的信号h(t)。
10.进一步地，所述时滞混沌系统采用含有时滞项的lorenz系统进行加密验证，所述含有时滞项的lorenz系统的系统方程如下：
[0011][0012]
其中，x,y,z分别表示时滞lorenz系统的三个状态变量，分别表示状态变量随时间的导数，τ为延迟时间。
[0013]
进一步地，步骤(2)中，所述加密的方程如下：
[0014][0015]
其中，u
2xi
、u
2yi
、u
2zi
为加密集u2(t)中的第i个数据的三个状态变量值，s
i
为加密后的一维向量，h
i
为解密后的一维向量，k1、k2、λ1、λ2为密钥。
[0016]
进一步地，所述储备池计算模块中神经网络状态方程如下：
[0017][0018]
其中，r(t)代表储备池状态矩阵，t表示时间，v'(t)是所述储备池计算模块输入的信号向量，α为学习率，bin为偏置参数，a是储层网络的邻接矩阵，win是输入端的加权矩阵。
[0019]
进一步地，所述储备池计算模块输出的信号向量v(t)计算公式如下：
[0020][0021]
其中，b
out
是偏置参数，w
out
是线性相关系数，r(t)是t时刻所述储备池计算模块的状态量，v'(t)是t时刻所述储备池计算模块输入的信号向量，v(t)是t+1时刻所述储备池计算模块输出的信号向量。
[0022]
进一步地，步骤(5)中，所述解密的方程如下：
[0023][0024][0025]
其中，v
xi
、v
yi
、v
zi
为信号向量v(t)在第i个时刻的状态变量值，k1、k2、λ1、λ2为密钥，s
i
为加密后的一维向量，h
i
为解密后的一维向量。
[0026]
训练后的储备池计算模块通过一个标量信号的传输即可模拟并同步解密加密系统从而加长了解密的长度，并且对一些高维度的时滞混沌系统加密信号也具备解密的效果，最后使用含有延时项的lorenz系统通过混沌掩盖的技术实现了图像的保密传输，并能正确有效地恢复出原有信息。
[0027]
本发明所述的基于机器学习储备池计算的保密通信系统，包括发送端和接收端，所述发送端包括时滞混沌系统、加密模块；所述接收端包括储备池计算前处理模块、储备池计算模块、解密模块；其中，
[0028]
所述时滞混沌系统，用于生成混沌信号u(t)，所述混沌信号u(t)包括训练集u1(t)和加密集u2(t)，所述训练集u1(t)用于发送至所述接收端；
[0029]
所述加密模块，用于利用所述加密集u2(t)对发送端发送的信号h(t)进行加密，生成加密信号s(t)；
[0030]
所述储备池计算前处理模块，用于对接收的加密集u2(t)中的信号进行归一化处理，得到信号向量v'(t)；
[0031]
所述储备池计算模块，用于获取所述储备池计算前处理模块归一化处理后的信
号，输出信号向量v(t)；获取加密集u2(t)中的某一个维度的标量信号，并用该信号替代信号向量v(t)中同一维度的信号，将得到的信号再次输入到所述储备池计算前处理模块中更新v'(t)；
[0032]
所述解密模块，用于获取所述加密信号s(t)，对所述加密信号s(t)和所述储备池计算模块同步输出的信号向量v(t)进行解密，得到发送端发送的信号h(t)。
[0033]
进一步地，所述加密模块的加密方程如下：
[0034][0035]
其中，u
2xi
、u
2yi
、u
2zi
为加密集u2(t)中的第i个数据的三个状态变量值，s
i
为加密后的一维向量，h
i
为解密后的一维向量，k1、k2、λ1、λ2为密钥。
[0036]
进一步地，所述储备池计算模块输出的信号向量v(t)计算公式如下：
[0037][0038]
其中，b
out
是偏置参数，w
out
是线性相关系数，r(t)是t时刻所述储备池计算模块的状态量，v'(t)是t时刻所述储备池计算模块输入的信号向量，v(t)是t+1时刻所述储备池计算模块输出的信号向量。
[0039]
进一步地，所述解密模块的解密方程如下：
[0040][0041][0042]
其中，v
xi
、v
yi
、v
zi
为响应系统在第i个时刻的状态变量值，k1、k2、λ1、λ2为密钥，s
i
为加密后的一维向量，h
i
为解密后的一维向量。
[0043]
有益效果：本发明采用储备池，克服了解密系统必须与混沌加密系统相一致的灵活性缺陷，实现对加密时滞混沌系统的信号同步，从而解密。
附图说明
[0044]
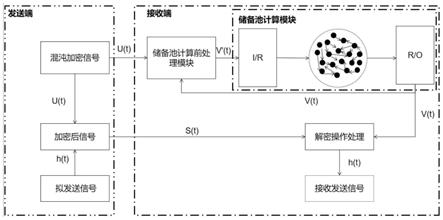
图1是本发明方法流程图及系统示意图；
[0045]
图2是含时滞项lorenz系统的同步预测拟合图，图2(a)是x和z维度真实值与预测值之间的误差；图(b)、(d)是储备池计算模块预测的数据和原有数据的拟合图，图c是预测数据在x和z维度的平面图；
[0046]
图3是
‘
lena’的图像的解密过程；图3(a)是原始图片，图3(b)是用含延时项的lorenz系统进行加密的后的图片，图3(c)是解密后的图片。
具体实施方式
[0047]
下面结合附图和实施例对本发明的技术方案作进一步的说明。
[0048]
请参见图1，其示出了本发明所述基于机器学习储备池计算的保密通信方法流程图及系统示意图。所述系统包括发送端和接收端，所述发送端包括时滞混沌系统、加密模块；所述接收端包括储备池计算前处理模块、储备池计算模块、解密模块；其中，
[0049]
所述时滞混沌系统，用于生成混沌信号u(t)，所述混沌信号u(t)包括训练集u1(t)和加密集u2(t)，所述训练集u1(t)用于发送至所述接收端；
[0050]
所述加密模块，用于利用所述加密集u2(t)对发送端发送的信号h(t)进行加密，生成加密信号s(t)；
[0051]
所述储备池计算前处理模块，用于对接收的加密集u2(t)中的信号进行归一化处理，得到信号向量v'(t)；
[0052]
所述储备池计算模块，用于获取所述储备池计算前处理模块归一化处理后的信号，输出信号向量v(t)；获取加密集u2(t)中的某一个维度的标量信号，并用该信号替代信号向量v(t)中同一维度的信号，将得到的信号再次输入到所述储备池计算前处理模块中更新v'(t)；
[0053]
所述解密模块，用于获取所述加密信号s(t)，对所述加密信号s(t)和所述储备池计算模块同步输出的信号向量v(t)进行解密，得到发送端发送的信号h(t)。
[0054]
为了直观表达出本发明实现的保密通信效果加密和解密效果，本实施例采用了图像加密的方式。以
‘
lena’的图像为例，其图像标准大小为256x256x3，再将这个图像排列成一个一维的向量原信号h。这里我们利用含有时滞项的lorenz系统进行加密验证。
[0055]
其中含时滞项的lorenz方程如方程(1)所示：
[0056][0057]
其中，x,y,z分别表示时滞lorenz系统的三个状态变量，分别表示状态变量随时间的导数，延迟时间τ设置为0.02s。
[0058]
首先采用四阶龙格塔库算法对偏微分方程求解，其中步长dt＝0.02s，采样得到2.1
×
105个数据点u(t),将u(t)分为两个部分，前2600个数据点作为训练集设为u1(t)，其余的数据作为加密数据u2(t)，首先对拟发送信号h进行加密，加密方程如下所示：
[0059][0060]
其中u
2xi
、u
2yi
、u
2zi
为混沌系统采样用于加密的数据u2的第i个数据的三个状态变量值，s
i
为加密后的一维向量，并发送给接收端，为了增加保密性能，k1、k2相对于λ1、λ2尽可能大，本次取k1＝200、k2＝150、λ1＝0.1、λ2＝0.15。
[0061]
为使接收端能够解密发送方发来的加密信号s
i
，接收端必须有一个和能和发送端混沌系统同步的一个系统，本实施例利用储备池计算的机器学习方法来实现同步，所述储备池计算模块的基本结构包括输入层，输出层和一个具有500个动态节点的储备池网络它的储备池网络的状态方程如方程(3)所示：
[0062][0063]
其中，r(t)代表储备池状态矩阵，t表示时间，v'(t)是输入储备池网络的输入向量。参数α为学习率，大小设为0.2，偏置参数bin＝1。除了输入向量v'(t)之外，储备池网络动态主要取决于矩阵win和a。其中，a是储层网络的邻接矩阵，win是输入端的加权矩阵，它们一般取正态分布矩阵。接下来我们需要定义储备池系统的输出向量v，它是储备池状态和输入向量的线性函数如方程(4)所示：
[0064][0065]
其中，偏置参数b
out
＝1，w
out
是学习阶段唯一需要调整并确定的参数。
[0066]
如图2所示为含时滞项lorenz系统的同步预测拟合图。其中，图2(a)中的
△
x表示的是真实信号u
x
与与预测信号v
x
之间的差值的绝对值，
△
z表示的是真实信号u
z
与与预测信号v
z
之间的差值的绝对值。图2(b)、2(d)中
‑
actual signal是原数据信号，
‑
reservoir output是储备池预测的各个维度的结果。
[0067]
在学习阶段，储备池网络首先基于方程(3)和v'(t)进行迭代训练，其中v'(t)是在训练阶段采用混沌系统采样的点(此时的v'(t)也即是u1(t)，训练得到的r(t)在舍弃起始的100个暂态点后以[bout；v'(t)；r(t)]的形式将其保存在训练集矩阵x中，将训练所用的u1(t)去掉前101个点后存放到矩阵y中在再用岭回归运算得到w
out
如方程(5)所示：
[0068]
w
out
＝yx
t
(xx
t
+λii)
ꢀꢀ
(5)
[0069]
其中λ为一个为了避免过拟合的偏置参数大小为1
×
10
‑8，ⅱ为单位矩阵。
[0070]
在同步解密阶段的储备池计算模块和学习阶段的过程类似，唯一不同的是利用u
2i
中的y维度作为驱动变量的替换输入端的v'
i
中y维度的值，而其他维度的输入值则由储备池网络的输出端v提供，这样通过方程(3)和(4)迭代运算，储备池计算模块可以以较小的误差同步混沌系统其他维度的信息，也即是两系统建立了同步关系，最后就可以通过同步信息v对加密信号s来进行解密。
[0071]
其中解密端的解密方程为方程(6)和(7)所示：
[0072][0073][0074]
其中，k1、k2、λ1、λ2为密钥，v
xi
、v
yi
、v
zi
分别为信号向量v(t)在第i个时刻的状态变量值，h为解密后的一维向量，再将其按照图片像素位置排序的逆过程将其转化为解密后图片的三原色值，并使用matlab展示如图3所示。