一种基于概率排序的低轨卫星切换方法与流程

1.本发明涉及低轨卫星通信网络领域，更具体地说，它涉及到低轨卫星切换方法。


背景技术：

2.由于低轨卫星星座与地面移动卫星用户之间的运动是高速和随机的，同时低轨卫星星座内的星间链路会随着卫星运行也发生变化。但是地面地动用户对信号质量的需求则要有稳定性，周期性、规律性，同时由于单个卫星转发器负载也会有差异，则急需一种可靠高效的方法来实现不同卫星的切换来保证链路通信质量，一种基于概率排序的低轨卫星切换方法得到业界广泛的关注。
3.低轨卫星通信网络的移动用户在进行链路通信的过程当中，由于低轨道卫星相对于移动用户的高速运动，卫星对移动用户的可视时间很短。随着移动用户卫星天线与低轨卫星间的通信仰角逐渐减小，用户与卫星之间的距离逐渐增大，导致信道质量逐渐变差，乃至不能通信。此时，用户与卫星的连接关系必须进行切换，用户需要从多颗覆盖他的卫星当中做出选择。切换可能发生在建链阶段，也可能发生在建链通信的过程中，无论哪种情况，都需要进行卫星的选择，因此提出一种基于概率排序的低轨卫星切换方法可以有效解决。


技术实现要素：

4.本发明的目的是提供一种基于概率排序的低轨卫星切换方法，通过对低轨卫星覆盖移动用户区域内所有卫星进行概率排序，得到低轨卫星切换的最优选择。
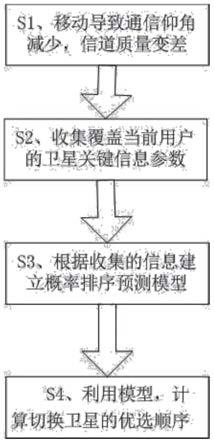
5.本发明的上述技术目的是通过以下技术方案得以实现的：一种基于概率排序的低轨卫星切换方法，包括以下步骤：首先用户或卫星的移动导致通信仰角减少，信道质量变差，即开始卫星切换。然后收集覆盖当前用户的低轨卫星关键信息参数，包括卫星距离，卫星的信号强度，卫星的通信覆盖时间，卫星当前负荷以及卫星的传播路径长度。接着，根据收集的信息建立概率排序预测模型。最后利用多元线性回归方程求解低轨卫星概率排序预测模型，得到切换卫星的优选顺序。
6.可选的，收集覆盖当前用户的低轨卫星关键信息参数，包括卫星距离，卫星的信号强度，卫星的通信覆盖时间，卫星当前负荷以及卫星的传播路径长度，其方法为：将当覆盖当前用户的n颗卫星中的第i颗卫星用排序效用函数y
i
(x)来描述，其中而影响y
i
(x)取值的参数有x有5个，分别是卫星距离x1，卫星的信号强度x2，卫星的通信覆盖时间x3，卫星当前负荷x4以及卫星的传播路径长度x5。5个参数的权重用q表示，分别是卫星距离权重q1，卫星的信号强度权重q2，卫星的通信覆盖时间权重q3，卫星当前负荷权重q4以及卫星的传播路径长度权重q5。
7.可选的，具体模型为：当覆盖当前用户的n颗卫星中的第i颗卫星的排序效用函数 y
i
(x)来描述，其中与覆盖当前用户的n颗卫星的关键信息参数是线性相关的关系，那么卫星的排序效用函数y的多元回归数学模型就可以表示为： y＝q1x1+q2x2+
q3x3+q4x4+q5x5，那么覆盖当前用户的n颗卫星中的第i颗卫星的关键信息参数为(x
1i
，x
2i
，x
3i
，x
4i
，x
5i
)，式中关键信息参数x第一个下脚标为卫星的编号，第二下脚标为关键信息参数的编号，则n颗卫星的数学模型为学模型为则n颗卫星的排序效用函数多元回归线性模型就可以改写成：y＝qx。
8.可选的，低轨卫星由于用户和卫星的相对高速移动，覆盖当前用户的低轨卫星关键信息参数都处于不断的变动中，但是变动的规律是与时间t相关并且存在着线性关系，因此，可以给出关键信息参数的若干个可能的取值，以卫星距离x1为例，在当前t时刻，随着距离变大或变小的趋势，可能的m个取值为 [x1]1，[x1]2，[x1]3，[x1]4……
[x1]
m
；取值正确的概率为p
1，
p2，p3，p4……
p
m
。由于无法确定卫星距离x1准确概率数字，所以也无法准确地计算其期望值。但是我们可以通过m个可能出现的数值以及这些数值出现概率的大小顺序，求得期望值e的可能取值范围。因此，利用期望值作为预测的参数值，是一个比较准确的方法。则，
[0009]
可选的，卫星信号强度x2取值也采取期望值计算，在当前t时刻，随着信号强度变大或变小的趋势，可能的m个取值为[x2]1，[x2]2，[x2]3，[x2]4……
[x2]
m
；取值正确的概率为p1，p2，p3，p4……
p
m
。由于无法确定卫星信号强度x2准确概率数字，所以也无法准确地计算其期望值。但是我们可以通过m个可能出现的数值以及这些数值出现概率的大小顺序，求得期望值e的可能取值范围。因此，利用期望值作为预测的参数值，是一个比较准确的方法。则，
[0010]
可选的，卫星通信覆盖时间x3取值也采取期望值计算，在当前t时刻，随着信号强度变大或变小的趋势，可能的m个取值为[x3]1，[x3]2，[x3]3，[x3]4……
[x3]
m
；取值正确的概率为p1，p2，p3，p4……
p
m
。由于无法确定卫星通信覆盖时间x3准确概率数字，所以也无法准确地计算其期望值。但是我们可以通过m个可能出现的数值以及这些数值出现概率的大小顺序，求得期望值e的可能取值范围。因此，利用期望值作为预测的参数值，是一个比较准确的方法。则，p
j
‑
p
j+1
≥0，p
j
≥0(j＝1，2，3...，m)
[0011]
可选的，卫星当前负荷x4取值也采取期望值计算，在当前t时刻，随着信号负载变大或变小的趋势，可能的m个取值为[x4]1，[x4]2，[x4]3，[x4]4……
[x4]
m
；取值正确的概率为
p1，p2，p3，p4……
p
m
。由于无法确定卫星通信覆盖时间x4准确概率数字，所以也无法准确地计算其期望值。但是我们可以通过m个可能出现的数值以及这些数值出现概率的大小顺序，求得期望值e的可能取值范围。因此，利用期望值作为预测的参数值，是一个比较准确的方法。则，
[0012]
可选的，卫星传播路径x5取值也采取期望值计算，在当前t时刻，随着卫星传播路径变大或变小的趋势，可能的m个取值为[x5]1，[x5]2，[x5]3， [x5]4……
[x5]
m
；取值正确的概率为p1，p2，p3，p4……
p
m
。由于无法确定卫星通信覆盖时间x5准确概率数字，所以也无法准确地计算其期望值。但是我们可以通过m个可能出现的数值以及这些数值出现概率的大小顺序，求得期望值e的可能取值范围。因此，利用期望值作为预测的参数值，是一个比较准确的方法。则，
[0013]
可选的，计算得到(x1，x2，x3，x4，x5)的输入值，根据系统的设计要求确定权重值 (q1，q2，q3，q4，q5)，如果五个关键参数同时考虑则q1＝q2＝q3＝q4＝q5＝1，如果某个因素不考虑，则q
i
＝0(i＝1，2，3，4，5)。计算得到(y1，y2，y3……
y
n
)的取值，并对取值进行排序，根据排序结果进行低轨卫星的切换。
[0014]
通过以下参照附图对本发明的示例性实施例的详细描述，本发明的其它特征及其优点将会变得清楚。
附图说明
图1是一种基于概率排序的低轨卫星切换方法流程图。
[0016]
图2是低轨卫星覆盖移动用户的示意图。
具体实施方式
[0017]
以下结合附图对本发明作进一步详细说明。
[0018]
本发明的上述技术目的是通过以下技术方案得以实现的：一种基于概率排序的低轨卫星切换方法，如附图1，包括以下步骤：首先用户或卫星的移动导致通信仰角减少，信道质量变差，即开始卫星切换。然后收集覆盖当前用户的低轨卫星关键信息参数，包括卫星距离，卫星的信号强度，卫星的通信覆盖时间，卫星当前负荷以及卫星的传播路径长度。接着，根据收集的信息建立概率排序预测模型。最后利用多元线性回归方程求解低轨卫星概率排序预测模型，得到切换卫星的优选顺序。
[0019]
可选的，如图2收集覆盖当前用户的低轨卫星关键信息参数，包括卫星距离，卫星的信号强度，卫星的通信覆盖时间，卫星当前负荷以及卫星的传播路径长度，其方法为：将当覆盖当前用户的n颗卫星中的第i颗卫星用排序效用函数y
i
(x)来描述，其中而影响y
i
(x)取值的参数有x有5个，分别是卫星距离x1，卫星的信号强度x2，卫星的通信覆盖时间x3，卫星当前负荷x4以及卫星的传播路径长度x5。5个参数的权重用q表示，分别是卫星距离权重q1，卫星的信号强度权重q2，卫星的通信覆盖时间权重q3，卫
星当前负荷权重q4以及卫星的传播路径长度权重q5。
[0020]
可选的，具体模型为：当覆盖当前用户的n颗卫星中的第i颗卫星的排序效用函数 y
i
(x)来描述，其中与覆盖当前用户的n颗卫星的关键信息参数是线性相关的关系，那么卫星的排序效用函数y的多元回归数学模型就可以表示为：y＝q1x1+q2x2+q3x3+q4x4+q5x5，那么覆盖当前用户的n颗卫星中的第i颗卫星的关键信息参数为(x
1i
，x
2i
，x
3i
，x
4i
，x
5i
)，式中关键信息参数x第一个下脚标为卫星的编号，第二下脚标为关键信息参数的编号，则n颗卫星的数学模型为学模型为则n颗卫星的排序效用函数多元回归线性模型就可以改写成：y＝qx。
[0021]
可选的，低轨卫星由于用户和卫星的相对高速移动，覆盖当前用户的低轨卫星关键信息参数都处于不断的变动中，但是变动的规律是与时间t相关并且存在着线性关系，因此，可以给出关键信息参数的若干个可能的取值，以卫星距离x1为例，在当前t时刻，随着距离变大或变小的趋势，可能的m个取值为 [x1]1，[x1]2，[x1]3，[x1]4……
[x1]
m
；取值正确的概率为 p1，p2，p3，p4……
p
m
。由于无法确定卫星距离x1准确概率数字，所以也无法准确地计算其期望值。但是我们可以通过m个可能出现的数值以及这些数值出现概率的大小顺序，求得期望值e的可能取值范围。因此，利用期望值作为预测的参数值，是一个比较准确的方法。则，
[0022]
可选的，卫星信号强度x2取值也采取期望值计算，在当前t时刻，随着信号强度变大或变小的趋势，可能的m个取值为[x2]1，[x2]2，[x2]3，[x2]4……
[x2]
m
；取值正确的概率为p1，p2，p3，p4……
p
m
。由于无法确定卫星信号强度x2准确概率数字，所以也无法准确地计算其期望值。但是我们可以通过m个可能出现的数值以及这些数值出现概率的大小顺序，求得期望值e的可能取值范围。因此，利用期望值作为预测的参数值，是一个比较准确的方法。则，
[0023]
可选的，卫星通信覆盖时间x3取值也采取期望值计算，在当前t时刻，随着信号强度变大或变小的趋势，可能的m个取值为[x3]1，[x3]2，[x3]3，[x3]4……
[x3]
m
；取值正确的概率为p1，p2，p3，p4……
p
m
。由于无法确定卫星通信覆盖时间x3准确概率数字，所以也无法准确
地计算其期望值。但是我们可以通过m个可能出现的数值以及这些数值出现概率的大小顺序，求得期望值e的可能取值范围。因此，利用期望值作为预测的参数值，是一个比较准确的方法。则，
[0024]
可选的，卫星当前负荷x4取值也采取期望值计算，在当前t时刻，随着信号负载变大或变小的趋势，可能的m个取值为[x4]1，[x4]2，[x4]3，[x4]4……
[x4]
m
；取值正确的概率为p1，p2，p3，p4……
p
m
。由于无法确定卫星通信覆盖时间x4准确概率数字，所以也无法准确地计算其期望值。但是我们可以通过m个可能出现的数值以及这些数值出现概率的大小顺序，求得期望值e的可能取值范围。因此，利用期望值作为预测的参数值，是一个比较准确的方法。则，
[0025]
可选的，卫星传播路径x5取值也采取期望值计算，在当前t时刻，随着卫星传播路径变大或变小的趋势，可能的m个取值为[x5]1，[x5]2，[x5]3， [x5]4……
[x5]
m
；取值正确的概率为p1，p2，p3，p4……
p
m
。由于无法确定卫星通信覆盖时间x5准确概率数字，所以也无法准确地计算其期望值。但是我们可以通过m个可能出现的数值以及这些数值出现概率的大小顺序，求得期望值e的可能取值范围。因此，利用期望值作为预测的参数值，是一个比较准确的方法。则，
[0026]
可选的，计算得到(x1，x2，x3x4，x5)的输入值，根据系统的设计要求确定权重值 (q1，q2，q3，q4，q5)，如果五个关键参数同时考虑则q1＝q2＝q3＝q4＝q5＝1，如果某个因素不考虑，则q
i
＝0(i＝1，2，3，4，5)。计算得到(y1，y2，y3……
y
n
)的取值，并对取值进行排序，根据排序结果进行低轨卫星的切换。
[0027]
综上所述，本发明具有以下有益效果：一种基于概率排序的低轨卫星切换方法解决了现有技术不能够有效的对低轨卫星切换进行最优选择，优化了卫星信道资源利用率和提高了低轨卫星通信网络的通信质量。
[0028]
以上所述仅是本发明的优选实施方式，本发明的保护范围并不仅局限于上述实施例，凡属于本发明思路下的技术方案均属于本发明的保护范围。应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理前提下的若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。