基于改进粒子群算法的室内可见光通信系统功率分配方法

1.本发明属于通信技术领域，具体涉及一种功率分配方法，可用于室内可见光通信系统，提高室内可见光通信系统的总数据速率。


背景技术：

2.随着物联网的兴起和人工智能技术的飞速发展，人类已经迈入了以“万物联网”为特征的智能时代。面对智能终端的普及移动新业务的发展，无线网络各个应用的需求呈爆发式增长，需要对现有的商用网络进行全面升级。在通信技术和实际业务的双需求下，只有寻找新的通信资源才能缓解目前的通信压力。
3.相比于频谱资源日益紧缺的传统的射频rf通信，可见光有着丰富的频谱资源，因此可见光通信vlc应运而生。可见光通信技术是以光波为载波的通信方式，作为一种新兴的通信技术，可见光通信技术中的信号源获取简单且兼具照明功能，成本低廉,且可见光通信无需频谱认证、无电磁干扰、传输速率高。随着led照明技术的进步，这一技术也同样被应用在室内照明系统中，将通信作为led照明系统的第二功能，实现了一种集照明和通信于一体的系统—室内可见光通信系统。
4.vlc应用场景极为广泛，在对电磁干扰敏感的环境，如医院、加油站等区域实现信号覆盖，有效弥补了其他技术的缺陷。此外，在矿井和地下车库等环境中，因为没有其他光源干扰，成本低廉的可见光通信更是具有天然优势；在某些需要保密通信的场景中，可见光通信同样因为其信号可以被建筑完全遮挡，即使在相邻区域也不会造成信息的泄漏。因为vlc有较低的实现成本，高安全性和良好的电磁兼容性等优点，在各个领域都引起了广泛关注。
5.为了进一步提高频谱利用率，提高系统吞吐量的实际需求，许多新型非正交多址接入技术被提出，包括功率域非正交接入技术noma，稀疏码多址接入技术scma，图样分割接入技术pdma和多用户共享接入技术musa等。相较于这些技术，其中功率域非正交多址接入noma使用较为广泛，以非正交方式复用相同功率域，并在用户接收端用串行干扰消除sic进行用户信息的分离与恢复，大幅度地提高了系统用户接入数量及总吞吐量。将noma引入室内vlc系统中，在vlc系统优势的基础上再次提高系统总吞吐量，迎合当今对通信技术的实际需求。
6.目前，基于noma的室内vlc系统中功率分配已有较成熟的研究，对于用户的功率分配方法分为全空间搜索功率分配方案fspa、固定功率分配方案fpa和分数阶功率分配方案ftpa，其中：
7.全空间搜索功率分配算法，其基本思想是在全空间遍历所有可能的功率分配方案，再对所有功率分配方案进行对比，直到找到使系统吞吐量达到最优的一种功率分配方案。该方案性能较好，但不足在于实现复杂度大且信令开销过大。
8.固定功率分配算法，是一种静态功率分配方案，其基本思想是首先将用户根据归一化信道增益从大到小进行排序，完成所有用户排序后，将相邻两个用户之间的发射功率
的比值作为一个固定值，通过迭代固定功率分配因子来对用户进行功率分配。该方案复杂度较低，但未考虑信道的时变性。
9.分数阶功率分配算法，其基本思想是根据每个用户信道增益的不同来分配功率，引用分数阶功率分配因子，通过调整分数阶功率分配因子改变用户间分配的功率，使信道条件较差的用户可以分配更多的功率。该方案充分考虑了信道的时变性，但很难找到最优功率分配因子。
10.因此，在室内可见光通信系统中，如何分配系统功率使系统的总数据速率得到显著提升是室内可见光通信系统需要解决的一个重要问题。


技术实现要素：

11.本发明的目的在于针对上述现有技术的不足，提出一种基于改进粒子群算法的室内可见光通信系统功率分配方法，求解室内可见光通信系统功率分配系数，并提高室内可见光通信系统的总数据速率。
12.为实现上述目的，本发明的技术方案包括如下步骤：
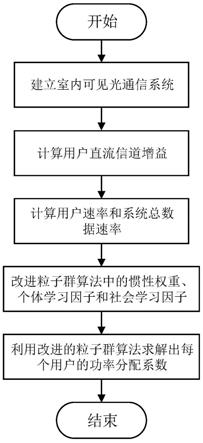
13.(1)建立室内可见光通信系统：
14.在天花板设置白光led，将白光led连接到服务器，构成发射机和照明光源，采用时分多址的方式发送光信号，并设置室内可见光通信系统的发射总功率p
elec
；
15.在led照射范围内放置多个光电探测器pd，即在接收端给每个用户设置1个光电探测器pd，用于从接受的光载波中提取发送信号；
16.(2)根据室内可见光通信系统下行链路信道模型，计算出每个用户的直流信道增益h
k
；
17.(3)根据非正交多址noma系统的数据速率模型，计算出每个用户的数据速率r
k
，根据每个用户的数据速率r
k
，计算系统的总数据速率r
sum
：
[0018][0019]
其中，a
k
为第k个用户的功率分配系数，r
k
(a1,...,a
k
,...,a
m
)代表用户k的数据速率关于k个功率分配系数的函数，m为系统服务的用户数；
[0020]
(4)对粒子群算法进行改进，即将线性递减惯性权重ω(t)改为非线性递减惯性权重ω(t)，两个常数学习因子c1和c2改为非线性异步变化的个体学习因子c1(t)和社会学习因子c2(t)，表示如下：
[0021][0022][0023][0024]
其中，ω
max
为最大惯性权重，ω
min
最小惯性权重，t为当前迭代，t
max
为最大迭代次
数；c
11
和c
12
分别为个体学习因子的初始值和最终迭代值,c
21
和c
22
分别为社会学习因子的初始值和最终迭代值；
[0025]
(5)根据系统的总数据速率r
sum
，利用改进的粒子群算法，求解出每个用户的功率分配系数a
k
；
[0026]
(6)根据功率分配系数a
k
给每个用户分配功率：
[0027]
本发明与现有方法相比有以下优点：
[0028]
1.本发明相较于传统粒子群算法求解功率分配系数，由于改进了惯性权重ω的选取方式，采用非线性递减惯性权重的方式，使惯性权重能够随着迭代过程的进行而呈非线性递减，有利于在搜寻功率分配系数的前期过程，确认功率分配系数的大致位置，并利于在搜寻功率分配系数的后期过程，确认功率分配系数的精确值。
[0029]
2.本发明相较于传统粒子群算法求解功率分配系数，由于采用非线性异步学习因子策略改进了个体学习因子c1和社会学习因子c2的选取方式，不仅使个体学习因子c1和社会学习因子c2能够随着迭代次数的不同而发生变化，而且可防止算法在搜寻功率分配系数的前期收敛速度过快陷入局部极值而产生的早熟收敛现象，提高了搜寻功率分配系数过程的收敛速度和系统总传输速率。
附图说明
[0030]
图1为本发明的实现流程图；
[0031]
图2为本发明中设置的室内可见光系统led与pd相对位置图；
[0032]
图3为本发明中设置的室内可见光通信系统的下行链路模型图；
[0033]
图4为使用传统粒子群算法求解功率分配系数的仿真图；
[0034]
图5为使用本发明求解功率分配系数的仿真图。
具体实施方式
[0035]
以下结合附图，对本发明的实施例和效果进一步详细说明
[0036]
参照图1，本实例的实现步骤如下：
[0037]
步骤1，建立室内可见光通信系统。
[0038]
1.1)发送端设置光源和服务器，发送端发送光信号：
[0039]
在天花板设置白光led，将白光led连接到服务器，构成发射机和照明光源，采用时分多址的方式发送光信号；
[0040]
根据白光led的最大功率设置室内可见光通信系统的发射总功率p
elec
，本实例取但不限于p
elec
＝1.25mw。
[0041]
1.2)接收端设置光电探测器pd，接收发送信号：
[0042]
在led照射范围内放置多个光电探测器pd，即在接收端给每个用户设置1个光电探测器pd，用于从接收的光载波中提取发送信号，该pd与led的相对位置如图2所示，由于系统中的串行干扰消除技术sic的复杂度较大，实际接收端用户数m取1到5，本实例取但不限于m＝3。
[0043]
步骤2，计算用户的直流信道增益。
[0044]
由图2中的led具体辐射范围和pd接收光信号的具体辐射范围，建立室内可见光通
信系统的下行链路模型图，如图3所示。
[0045]
根据图3所示的室内可见光通信系统下行链路信道模型，计算出每个用户的直流信道增益h
k
：
[0046][0047]
其中，r
p
为pd响应度，a为pd的有效接收面积，h为pd与led的垂直距离，t
s
光滤波器增益，ψ
fov
为pd的视场角，r
k
为第k个pd与led的水平距离，ψ
k
为第k个pd相对于轴线的入射角，m为朗伯模型发射阶数，计算公式为：m为朗伯模型发射阶数，计算公式为：为led的半功率角；g(ψ
k
)为光集中器增益，其公式为：
[0048][0049]
其中，n为光学集中器反射系数。
[0050]
步骤3，计算用户数据速率r
k
和系统总数据速率r
sum
。
[0051]
3.1)根据非正交多址noma系统的数据速率模型，计算出每个用户的数据速率r
k
：
[0052]
所述非正交多址noma系统的数据速率模型分为两种情况，分别为基于完美信道csi情况下的数据速率模型和基于非完美信道icsi的情况下的数据速率模型，本实例取但不限于基于非完美信道icsi的情况下的数据速率模型，其数据速率r
k
的计算公式如下：
[0053][0054]
其中，m为系统服务的用户数，b为信道带宽，ε为残留干扰因子，a
k
为第k个用户的功率分配系数，ρ为发送信噪比，ρ＝p
elec
/n0b，n0为噪声功率谱密度；
[0055]
3.2)根据每个用户的数据速率r
k
，计算系统的总数据速率r
sum
：
[0056][0057]
其中，r
k
(a1,...,a
k
,...,a
m
)代表用户k的数据速率关于k个功率分配系数的函数。
[0058]
步骤4，改进粒子群算法中的惯性权重和学习因子。
[0059]
粒子群算法是一个用来求解目标优化问题和非线性规划问题的算法，算法的核心是将粒子群中各个粒子的位置抽象为目标优化问题的解，在迭代过程中，通过动态调整各个粒子的位置和速度，搜寻个体最优位置和群体最优位置。传统粒子群算法在调整粒子的位置和速度的过程中，采用线性递减惯性权重的方法，同时将学习因子设为常数，这样容易使算法收敛速度降低、陷入局部最优，并产生早熟现象，最终导致求解最优值的过程较长。为了解决上述缺陷，对实例粒子群算法中的惯性权重和学习因子进行如下改进：
[0060]
4.1)将传统粒子群算法中的线性递减惯性权重ω(t)改为非线性递减惯性权重ω(t)，表示如下：
[0061][0062]
其中，ω
max
为最大惯性权重，ω
min
最小惯性权重，t为当前迭代，t
max
为最大迭代次数；
[0063]
4.2)将传统粒子群算法中的两个常数学习因子c1和c2，改为非线性异步变化的个体学习因子c1(t)和社会学习因子c2(t)，表示如下：
[0064][0065][0066]
其中，c
11
和c
12
分别为个体学习因子的初始值和最终迭代值,c
21
和c
22
分别为社会学习因子的初始值和最终迭代值。
[0067]
步骤5，利用改进的粒子群算法求解功率分配系数a
k
[0068]
5.1)初始化粒子群算法参数：
[0069]
设粒子群中粒子总数n，最大迭代次数t
max
，个体学习因子的初始值c
11
和最终迭代值c
12
,社会学习因子的初始值c
21
和c
22
，最大惯性权重ω
max
，最小惯性权重ω
min
；
[0070]
令初始迭代次数t＝0，并随机初始化粒子i的位置和速度
[0071][0072][0073]
其中，表示第i个粒子第0次迭代的第k维分量的值，ik代表第i个粒子的第k维分量,i∈[1,n],k∈[1,m]；
[0074]
5.2)确定适应度函数
[0075]
5.2.1)根据非正交多址noma系统数据速率模型，将系统数据速率最大化问题建模为非线性优化问题，表示如下：
[0076][0077]
5.2.2)在满足约束条件下，将粒子群算法的适应度函数表示如下：
[0078][0079]
5.3)根据适应度函数计算n个粒子的初始适应度值，将其作为当前各个粒子的局部最优值，并令初始局部最优值的位置：
[0080]
5.4)对所有粒子的初始适应度值进行比较，找到最大的初始适应度值，将其作为
粒子群的初始全局最优值，将最大初始适应度值的位置作为初始全局最优值的位置g0；
[0081]
5.5)利用改进后的惯性权重、个体学习因子和社会学习因子公式计算当前迭代过程中的惯性权重ω(t)、个体学习因子c1(t)和社会学习因子c2(t)：
[0082][0083][0084][0085]
5.6)更新当前迭代过程中各个粒子的速度和位置
[0086][0087][0088]
其中，rand1为[0,1]的随机数；
[0089]
5.7)根据粒子的位置计算当前每个粒子的适应度值并更新每个粒子的局部最优值及局部最优值所在位置
[0090]
5.7.1)根据粒子的位置计算当前每个粒子的适应度值：
[0091][0092]
其中，表示第i个粒子第t+1次迭代的第k维分量的值；
[0093]
5.7.2)更新每个粒子的局部最优值及局部最优值所在位置即判断当前粒子的适应度值是否大于历史适应度值
[0094]
若大于，则将当前适应度值作为局部最优值并将当前适应度值的位置作为局部最优值所在的位置
[0095]
否则，保持局部最优值及局部最优值的位置不变；
[0096]
5.8)更新粒子群的全局最优值gb
t+1
和全局最优值所在位置g
t+1
：
[0097]
5.8.1)比较当前所有粒子的适应度值找到粒子群中最大的适应度值
[0098]
5.8.2)判断当前最大的适应度值是否大于历史全局最优值gb
t
,gb
t
‑1,
…
,gb0：
[0099]
若大于，则用当前最大的适应度值作为全局最优值gb
t+1
，并将当前适应度值的位置作为全局最优值的位置g
t+1
；
[0100]
否则，保持全局最优值gb
t+1
及全局最优值的位置g
t+1
不变；
[0101]
5.9)判断当前迭代次数是否小于最大迭代次数t
max
，
[0102]
若小于，则迭代次数加1，并返回5.5；
[0103]
否则，输出全局最优值所在的位置即得到了系统的功率分配系数a1,
…
,a
k
,
…
,a
m
。
[0104]
步骤6，根据功率分配系数a
k
给每个用户分配功率：
[0105]
以下结合仿真实验，对本发明的技术效果作进一步详细说明：
[0106]
1.仿真条件
[0107]
在长和宽都为6米，高度为3米的房间内，白光led在天花板的坐标为(3,3,3),pd位置为(3,0,0)，(3,1,0)，(3,3,0)。
[0108]
传统粒子群算法的仿真参数，如表1所示，
[0109]
表1：传统粒子群算法仿真参数设置
[0110]
参数名称取值参数名称取值粒子群数n40最大迭代次数t
max
100最大惯性权值ω
max
0.9最小惯性权值ω
min
0.4个体学习因子c12社会学习因子c21
[0111]
本发明的仿真参数，如表2所示：
[0112]
表2：本发明仿真参数设置
[0113]
参数名称取值参数名称取值粒子群数n40最大迭代次数100最大惯性权重ω
max
0.9最小惯性权重ω
min
0.4个体学习因子c1的初始值c
11
2个体学习因子c1的最终迭代值c
12
1社会学习因子c2的初始值c
21
1社会学习因子c2的最终迭代值c
221[0114]
2.仿真内容和结果分析：
[0115]
仿真1，在上述仿真条件下，使用传统粒子群算法求解功率分配系数，即系统最大总数据速率r
sum
的迭代过程，结果如图4所示。从图4可见，使用传统粒子群算法寻找系统最大总数据速率的收敛速率较低，迭代次数多且多次陷入局部最优。当曲线最终趋于平缓时，即迭代25次，才得到了系统最大的总数据速率r
sum
＝10.27*107bps，此时r
sum
对应的功率分配系数为a1＝0.9,a2＝6.5534
×
10
‑9,a3＝2.0478
×
10
‑9。
[0116]
仿真2，在上述仿真条件下，使用本发明求解功率分配系数，即系统最大总数据速率r
sum
的迭代过程，其结果如图5所示。由图5可见，使用本发明寻找系统最大总数据速率的收敛速率较高且迭代次数少，仅迭代10次曲线便趋于平缓，得到了系统最大的总数据速率r
sum
＝10.34*107bps，此时r
sum
对应的功率分配系数a1＝0.9,a2＝7.3516
×
10
‑6,a3＝6.4629
×
10
‑6。
[0117]
综上所述，使用本发明求解室内可见光通信系统的功率分配系数相较于利用传统粒子群算法求解功率分配系数的方法，由于改进了惯性权重ω、个体学习因子c1和社会学习因子c2的选取方式，有效了提高系统最大的总数据速率，并且提高了搜寻最优功率分配系数的收敛速度且避免了陷入局部最优的情况。