基于三粒子GHZ纠缠态的单态三方半量子密钥协商方法

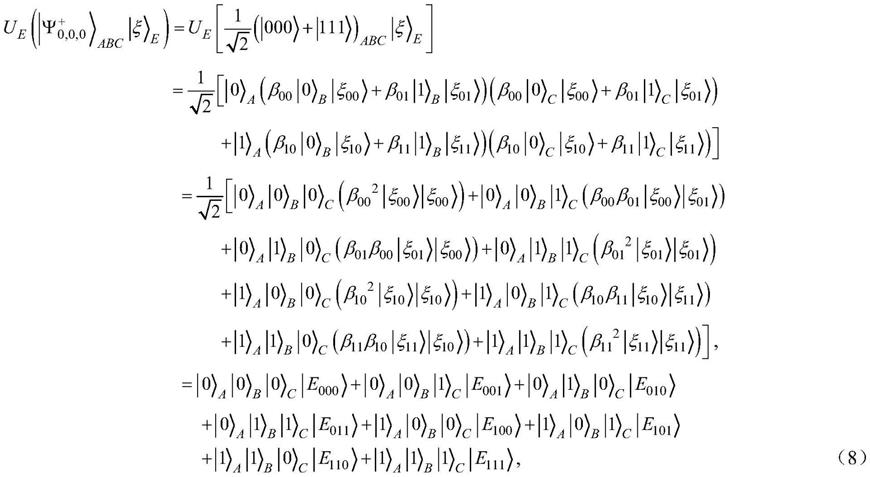
基于三粒子ghz纠缠态的单态三方半量子密钥协商方法
技术领域
1.本发明涉及量子密码学领域。本发明设计一种基于三粒子ghz纠缠态的单态三方半量子密钥协商方 法，实现一个量子方和两个仅拥有有限量子能力的经典方在量子信道上平等地促成一个共享密钥的产生。


背景技术：

2.1984年，bennett和brassard[1]提出了第一个量子密钥分配(quantum key distribution，qkd)方法， 这意味着量子密码学的诞生。经典密码学的安全性取决于解决数学问题的计算复杂性；与经典密码学不 同的是，量子密码学依赖量子不可克隆定理、海森堡测不准原理等物理定律获得理论上的无条件安全性。 自从量子密码学诞生以来，许多人一直致力于研究它。例如，量子密钥协商(quantum key agreement， qka)近年来成为量子密码学的一个热门话题。在qkd，一方通过量子信道将她的密钥分配给其他方； 与qkd不同的是，qka允许所有参与者平等地影响共享密钥的产生，意味着共享密钥不能由所有参与 者的任何非平凡子集决定。
[0003]
2004年，zhou等人[2]利用量子隐形传态技术提出了第一个qka方法。然而，tsai和hwang[3]随 后指出了zhou等人方法中的一个缺点，即共享密钥可以由任意参与者完全确定。后来，hsueh和chen[4] 提出了一个基于最大纠缠态的qka方法。2011年，chong等人[5]对文献[4]中的两个方法的缺陷进行了 改进。2013年，shi和zhong[6]利用bell态和纠缠交换提出了第一个多方qka方法；liu等人[7]指出 文献[6]中的方法无法抵抗参与者攻击，并提出了一种新的基于单粒子的多方qka方法；yin等人[8]提 出了一种基于两光子纠缠的三方qka方法。2014年，xu等人[9]提出了一种新颖的基于ghz态的多方 qka方法。2016年，sun等人[10]提出了一种基于团簇态的高效多方qka方法；zhu等人[11]指出，文 献[8]中的方法是不安全的，因为两个不忠诚的参与者可以合谋单独确定共享密钥，并提出一种方法对该 漏洞进行改进。2020年，wang等人[12]提出了一个基于量子傅里叶变换的三方qka方法。
[0004]
上述qka方法总是要求所有方拥有完全的量子能力，这在某些情形下是不实际的。为了减轻部分 参与方的量子态制备和量子态测量的负担，boyer等人[13-14]首次提出了半量子密码的概念，即允许部 分参与方仅具有有限的量子能力，如用z基(即{|0》,|1》})测量量子比特、制备新的量子比特处于z基、 不干扰地发送量子比特以及通过不同的延迟线重新排列量子比特。自从半量子密码概念诞生以来，许多 学者将其应用于不同的量子密码学分支来设计不同种类的半量子密码方法，如半量子密钥分配 (semiquantum key distribution，sqkd)方法[13-18]、半量子隐私比较(semiquantum private comparison， sqpc)方法[19,20]，半量子秘密共享(semiquantum secret sharing，sqss)方法[21-23]、半量子受控安 全直接通信(semiquantum controlled secure direct communication，sqcsdc)方法[24]、半量子对话方法 [24,25]、半量子密钥协商(semiquantum key agreement，sqka)方法[24,26,27]等。关于sqka，2017 年，shukla等人[24]提出了一种基于bell态的两方sqka方法；liu等人[26]提出了一种基于代理量子 计算的多方sqka方法。
2020年，zhou等人[27]提出了一个基于四粒子团簇态的三方sqka方法。
[0005]
基于上述分析，为了实现一个量子方和两个经典方在量子信道上平等地促成共享私钥的生成这一目标，本发明首先提出了一种新颖的单态三方sqka方法，仅采用一种三粒子ghz纠缠态作为初始量子资源。然后，本发明将其推广到n方情形，仅使用一种n粒子ghz纠缠态作为初始量子资源，可以实现一个量子方和n-1个经典方在量子信道上平等地促成共享私钥的生成这一目标。
[0006]
参考文献
[0007]
[1]bennett,c.h.,brassard,g.:quantumcryptography:publickeydistributionandcointossing.in:proceedingsofieeeinternationalconferenceoncomputers,systems,andsignalprocessing,bangalore,india,pp.175-179(1984)
[0008]
[2]zhou,n.r.,zeng,g.h.,xiong,j.:quantumkeyagreementprotocol.electron.lett.40,1149-1150(2004)
[0009]
[3]chong,s.k.,tsai,c.w.,hwang,t.:improvementon“quantumkeyagreementprotocolwithmaximallyentangledstates”.int.j.theor.phys.50,1793-1802(2011)
[0010]
[4]shi,r.h.,zhong,h.:multi-partyquantumkeyagreementwithbellstatesandbellmeasurements.quantuminf.process.12,921-932(2013)
[0011]
[5]liu,b.,gao,f.,huang,w.,wen,q.y.:multipartyquantumkeyagreementwithsingleparticles.quantuminf.process.12,1797-1805(2013)
[0012]
[6]yin,x.r.,ma.w.p.,liu,w.y.:three-partyquantumkeyagreementwithtwo-photonentanglement.int.j.theor.phys.52:3915-3921(2013)
[0013]
[7]xu,g.b.,wen,q.y.,gao,f.,qin,s.j.:novelmultipartyquantumkeyagreementprotocolwithghzstates.quantuminf.process.13,2587-2594(2014)
[0014]
[8]sun,z.y.,yu,j.p.,wang,p.:efficientmulti-partyquantumkeyagreementbyclusterstates.quantuminf.process.15,373-384(2016)
[0015]
[9]zhu,z.c.,hu,a.q.,fu,a.m.:participantattackonthree-partyquantumkeyagreementwithtwo-photonentanglement.int.j.theor.phys.55:55-61(2016)
[0016]
[10]wang,w.,zhou,b.m.,zhang,l.:thethree-partyquantumkeyagreementprotocolwithquantumfouriertransform.int.j.theor.phys.59,1944-1955(2020)
[0017]
[11]boyer,m.,kenigsberg,d.,mor,t.:quantumkeydistributionwithclassicalbob.phys.rev.lett.99(14):140501(2007)
[0018]
[12]boyer,m.,gelles,r.,kenigsberg,d.,mor,t.:semiquantumkeydistribution.phys.rev.a79(3):032341(2009)
[0019]
[13]li,c.,yu,k.,kao,s.,hwang,t.:authenticatedsemi-quantumkeydistributionswithoutclassicalchannel.quantuminf.process.15(7),2881-2893(2016)
[0020]
[14]meslouhi,a.,hassouni,y.:cryptanalysisonauthenticatedsemi-quantumkeydistributionprotocolusingbellstates.quantuminf.process.16(1),18(2017)
[0021]
[15]zou,x.f.,qiu,d.w.,zhang,s.y.,mateus,p.:semiquantumkeydistributionwithoutinvokingtheclassicalparty’smeasurementcapability.quantuminf.process.14(8),2981-2996(2015)
[0022]
[16]ye,t.y.,ye,c.q.:measure-resendsemi-quantumprivatecomparisonwithoutentanglement.int.j.theor.phys.57(12),3819-3834(2018)
[0023]
[17]lin,p.h.,hwang,t.,tsai,c.w.:efficientsemi-quantumprivatecomparisonusingsinglephotons.quantuminf.process.18,207(2019)
[0024]
[18]xie,c.,li,l.,qiu,d.:anovelsemi-quantumsecretsharingschemeofspecificbits.int.j.theor.phys.54,3819-3824(2015)
[0025]
[19]gao,x.,zhang,s.,chang,y.:cryptanalysisandimprovementofthesemi-quantumsecretsharingprotocol.int.j.theor.phys.56,1-9(2017)
[0026]
[20]ye,t.y.,ye,c.q.:circularsemi-quantumsecretsharingusingsingleparticles.commun.theor.phys.70(12),15-25(2018)
[0027]
[21]shukla,c.,thapliyal,k.,pathak,a.:semi-quantumcommunication:protocolsforkeyagreement,controlledsecuredirectcommunicationanddialogue.quantuminf.process.16,295(2017)
[0028]
[22]ye,t.y.,ye,c.q.:semi-quantumdialoguebasedonsinglephotons.int.j.theor.phys.57(5):1440-1454(2018)
[0029]
[23]liu,w.j.,chen,z.y.,ji,s.,wang,h.b.,zhang,j.:multi-partysemi-quantumkeyagreementwithdelegatingquantumcomputation.int.j.theor.phys.56,3164-3174(2017)
[0030]
[24]zhou,n.r.,zhu,k.n.,wang,y.q.:three-partysemi-quantumkeyagreementprotocol.int.j.theor.phys.59,663-676(2020)
[0031]
[25]cai,q.y.:eavesdroppingonthetwo-wayquantumcommunicationprotocolswithinvisiblephotons.phys.lett.a351(1-2):23-25(2006)
[0032]
[26]gisin,n.,ribordy,g.,tittel,w.,zbinden,h.:quantumcryptography.rev.mod.phys.74(1):145-195(2002)
[0033]
[27]deng,f.g.,zhou,p.,li,x.h.,etal.:robustnessoftwo-wayquantumcommunicationprotocolsagainsttrojanhorseattack.https://arxiv.org/abs/quant-ph/0508168(2005)
[0034]
[28]li,x.h.,deng,f.g.,zhou,h.y.:improvingthesecurityofsecuredirectcommunicationbasedonthesecrettransmittingorderofparticles.phys.rev.a74:054302(2006)
[0035]
[29]sun,z.w.,zhang,c.,wang,b.h.,li,q.,long,d.y.:improvementson“multipartyquantumkeyagreementwithsingleparticles”.quantuminf.process.12,3411(2013)
[0036]
[30]cabello,a.:quantumkeydistributionintheholevolimit.phys.rev.lett.85:5635(2000)
[0037][0038][0039]


技术实现要素：

[0040]
本发明的目的是设计一种基于三粒子ghz纠缠态的单态三方半量子密钥协商方法，实现一个量子方 和两个仅拥有有限量子能力的经典方在量子信道上平等地促成一个共享密钥的产生。
[0041]
基于三粒子ghz纠缠态的单态三方半量子密钥协商方法，共包括以下六个过程：
[0042]
s1)alice、bob和charlie分别使用量子随机数生成器(quantum random number generator，qrng) 生成原始随机密钥和其中其中且r＝1,2,
…
,n。alice、bob和charlie各自计算相应原 始随机密钥的哈希值，并将结果公布给另外两方。用和分别表示和的哈希值。
[0043]
s2)alice制备了8n个ghz纠缠态都处于然后，alice将它们分为三个序列： 其中是s
l
的第j个粒子，l＝a,b,c且j＝1,2,
…
,8n。具体地说，这些ghz纠缠 态的所有第一、第二和第三粒子分别形成有序序列sa、sb和sc。alice将sb(sc)中的粒子逐个发送 给bob(charlie)。在alice将第一个粒子发送给bob(charlie)后，她仅在收到前一个粒子后才发送下 一个粒子。
[0044]
s3)对于接收到的sb(sc)的第j(j＝1,2,
…
,8n)个粒子，bob(charlie)随机执行以下两个操 作中的一个：
①
ctrl操作，即将第j个接收到的粒子直接无干扰返回给alice；
②
sift操作，即使 用z基测量第j个接收到的粒子以获得测量结果制备一个新粒子处于他(她)所发现的状 态，并将其重新发送给alice。bob(charlie)选择进行sift的粒子只有4n个。bob(charlie)记下选 择进行sift时得到的
[0045]
s4)bob(charlie)告诉alice他(她)sb(sc)中选择进行sift的位置。alice根据bob和charlie 的操作对接收到的粒子执行不同的操作，如表1所示。情形a、情形b和情形c用于检查sb和sc的传 输是否安全；情形d不仅用于检查sb和sc的传输安全性，还用于密钥协商。情形d发生的位置有2n个； alice、bob和charlie在这2n个位置中随机选择n个来检查sb和sc的传输安全性。
[0046]
在情形a中，对于bob和charlie都选择进行ctrl的位置，alice执行操作1。如果不存在eve， alice的测量结果应为
[0047]
在情形b中，对于bob选择进行ctrl且charlie选择进行sift的位置，alice执行操作2。如果 不存在eve，charlie对原始粒子的测量结果、alice对来自bob的粒子的测量结果以及alice对自己手中 相应粒子的测量结果都应相同；为了检测是否存在eve，charlie需要告诉alice她的测量结果；
[0048]
在情形c中，对于bob选择进行sift且charlie选择进行ctrl的位置，alice执行操
作3。如果 不存在eve，bob对原始粒子的测量结果、alice对来自charlie的粒子的测量结果以及alice对自己手中 相应粒子的测量结果都应相同；为了检测是否存在eve，bob需要告诉alice他的测量结果；
[0049]
在情形d中，对于bob选择进行sift且charlie选择进行sift的位置，alice执行操作4。如果不 存在eve，bob对原始粒子的测量结果、charlie对原始粒子的测量结果以及alice对自己手中相应粒子 的测量结果都应相同；alice对来自bob(charlie)的粒子的测量结果应该与bob(charlie)制备的新粒 子的状态相同。为了检查是否存在eve，bob和charlie需要告诉alice他们所选中的n个位置的测量结 果；
[0050]
如果这四种情形中的任何一种错误率异常高，通信将被立即终止；否则，通信将被继续。
[0051]
表1与bob和charlie的操作相对应的alice的操作
[0052][0053]
操作1：alice利用ghz基测量来自bob的粒子、来自charlie的粒子以及自己手中相应的粒子；
[0054]
操作2：alice利用z基测量来自bob的粒子和她自己手中相应的粒子；
[0055]
操作3：alice利用z基测量来自charlie的粒子和她自己手中相应的粒子；
[0056]
操作4：alice利用z基测量来自bob的粒子、来自charlie的粒子以及她自己手中的相应粒子。
[0057]
s5)对于情形d，n个用于安全检测的粒子被丢弃后，剩余n个粒子被用于密钥协商。为简便起见， 它们被称为info粒子。alice手上的info粒子的测量结果的比特值表示为类似地，表示mb中对应info粒子的比特值，表示 mc对应info粒子的比特值。显然，存在alice计算其中 r＝1,2,
…
,n，并向bob和charlie公布其中与此同时，bob计算 并向alice和charlie公布其中charlie计算 并向alice和bob公布其中
[0058]
s6)根据alice从中提取然后，alice计算的哈希 值得到结果如果和都成立，alice将接受 为最终的共享密钥。
[0059]
bob从和中推导出然后，bob计算的哈希值得到结 果如果和都成立，bob将接受
为最终的共享密钥。
[0060]
charlie从和中推导出然后，charlie计算的哈希值得 到结果如果和都成立，charlie将接受为最终的共享密钥。
[0061]
如果alice、bob和charlie中的任何一个拒绝将作为最终共享密钥，通信将 被终止并从头开始。
附图说明
[0062]
图1是本发明提出的单态三方sqka方法的流程图；图2是eve对sb和sc的粒子发起的由两个酉 操作ue和uf表示的纠缠-测量攻击。
具体实施方式
[0063]
下面结合实施例对本发明的技术方案做进一步描述。
[0064]
1单态三方半量子密钥协商方法描述
[0065]
三粒子ghz态是三量子比特最大纠缠态，定义为
[0066][0067]
其中s,t∈{0,1}。
[0068]
假设alice拥有无限的量子能力，而bob和charlie是具有有限量子能力的两个经典方。alice、bob和 charlie希望通过量子通道协商一个共享密钥，条件是每个参与者平等地促成该共享密钥的生成，即该共 享密钥不能由他们的任何非平凡子集完全决定。为了实现这一目标，本发明采用三粒子ghz纠缠态 作为量子资源来设计一个具体步骤描述如下的单态三方sqka方法。为清晰起见，其流程图 在图1中给出。在整个方法中，经典比特0对应于量子态|0》，而经典比特1对应于量子态|1》。
[0069]
s1)alice、bob和charlie分别使用qrng生成原始随机密钥和其中 且 r＝1,2,
…
,n。alice、bob和charlie各自计算相应原始随机密钥的哈希值，并将结果公布给另外两方。 用和分别表示和的哈希值。
[0070]
s2)alice制备了8n个ghz纠缠态都处于然后，alice将它们分为三个序列： 其中是s
l
的第j个粒子，l＝a,b,c且j＝1,2,
…
,8n。具体地说，这些ghz纠缠 态的所有第一、第二和第三粒子分别形成有序序列sa、sb和sc。alice将sb(sc)中的粒子逐个发送 给bob(charlie)。在alice将第一个粒子发送给bob(charlie)后，她仅在收到前一个粒子后才发送下 一个粒子。
[0071]
s3)对于接收到的sb(sc)的第j(j＝1,2,
…
,8n)个粒子，bob(charlie)随机执行以下两个操 作中的一个：
①
ctrl操作，即将第j个接收到的粒子直接无干扰返回给alice；
②
sift操作，即使 用z基测量第j个接收到的粒子以获得测量结果制备一个新粒子处于他(她)所发现的状 态，并将其重新发送给alice。bob(charlie)选择进行sift的粒子只有4n个。bob(charlie)记下选 择进行sift时得到的
[0072]
s4)bob(charlie)告诉alice他(她)sb(sc)中选择进行sift的位置。alice根据bob和charlie 的操作对接收到的粒子执行不同的操作，如表1所示。情形a、情形b和情形c用于检查sb和sc的传 输是否安全；情形d不仅用于检查sb和sc的传输安全性，还用于密钥协商。情形d发生的位置有2n个； alice、bob和charlie在这2n个位置中随机选择n个来检查sb和sc的传输安全性。
[0073]
在情形a中，对于bob和charlie都选择进行ctrl的位置，alice执行操作1。如果不存在eve， alice的测量结果应为
[0074]
在情形b中，对于bob选择进行ctrl且charlie选择进行sift的位置，alice执行操作2。如果 不存在eve，charlie对原始粒子的测量结果、alice对来自bob的粒子的测量结果以及alice对自己手中 相应粒子的测量结果都应相同；为了检测是否存在eve，charlie需要告诉alice她的测量结果；
[0075]
在情形c中，对于bob选择进行sift且charlie选择进行ctrl的位置，alice执行操作3。如果 不存在eve，bob对原始粒子的测量结果、alice对来自charlie的粒子的测量结果以及alice对自己手中 相应粒子的测量结果都应相同；为了检测是否存在eve，bob需要告诉alice他的测量结果；
[0076]
在情形d中，对于bob选择进行sift且charlie选择进行sift的位置，alice执行操作4。如果不 存在eve，bob对原始粒子的测量结果、charlie对原始粒子的测量结果以及alice对自己手中相应粒子 的测量结果都应相同；alice对来自bob(charlie)的粒子的测量结果应该与bob(charlie)制备的新粒 子的状态相同。为了检查是否存在eve，bob和charlie需要告诉alice他们所选中的n个位置的测量结 果；
[0077]
如果这四种情形中的任何一种错误率异常高，通信将被立即终止；否则，通信将被继续。
[0078]
s5)对于情形d，n个用于安全检测的粒子被丢弃后，剩余n个粒子被用于密钥协商。为简便起见， 它们被称为info粒子。alice手上的info粒子的测量结果的比特值表示为类似地，表示mb中对应info粒子的比特，表示mc对应info粒子的比特。显然，存在
[0079][0080]
alice计算
[0081][0082]
其中r＝1,2,
…
,n，并向bob和charlie公布其中与此同时，bob计算
[0083]
[0084]
并向alice和charlie公布其中charlie计算
[0085][0086]
并向alice和bob公布其中
[0087]
s6)根据alice从中提取然后，alice计算的哈希 值得到结果如果和都成立，alice将接受为最终的共享密钥。
[0088]
bob从和中推导出然后，bob计算的哈希值得到结 果如果和都成立，bob将接受为最终的共享密钥。
[0089]
charlie从和中推导出然后，charlie计算的哈希值得 到结果如果和都成立，charlie将接受为最终的共享密钥。
[0090]
如果alice、bob和charlie中的任何一个拒绝将作为最终共享密钥，通信将 被终止并从头开始。
[0091]
2安全性分析
[0092]
2.1外部攻击
[0093]
在本发明的单态三方sqka方法中，为了获得密钥kf，外部窃听者eve可能在sb和sc的粒子的 整个传输过程中通过发动一些著名的攻击来尽力获取一些有用的信息，如特洛伊木马攻击、纠缠-测量 攻击、测量-重发攻击和截获-重发攻击。
[0094]
(1)特洛伊木马攻击
[0095]
在本发明的单态三方sqka方法中，sb(sc)的粒子在alice和bob(charlie)之间来回传输， 因此应该采取措施克服eve的特洛伊木马攻击，包括不可见光子窃听攻击[28]和延迟光子特洛伊木马攻 击[29,30]。正如文献[30,31]所指出的，为了抵御不可见光子窃听攻击，bob(charlie)可以在他(她) 的设备前放置一个波长滤波器来消除非法光子信号；为了防止延迟光子特洛伊木马攻击，bob(charlie) 可以采用光子数分割器(pns:50/50)将每个样本信号分成两部分，使用正确的测量基对它们进行测量， 并检测多光子率是否异常高。
[0096]
(2)纠缠-测量攻击
[0097]
eve对sb和sc的粒子发起的纠缠-测量攻击可以用两个酉操作ue和uf来建模，其中ue攻击从 alice发送给bob和charlie的粒子，uf攻击从bob和charlie返回给alice的粒子，并且ue和uf共享 一个初始状态为|ξ》e的共同探测空间。共享探测态允许eve根据从ue获得的信息对返回的粒子发起攻 击(如果eve没有利用这一点，“共享探测态”可以被认为是由两个独立探测态组成的复合系统)[13,14]。 eve使uf依赖于执行ue后的测量的任何攻击都可以由ue和uf通过受控门实现。eve对sb和sc的粒 子发起的纠缠-测量攻击可用图2表示。
[0098]
定理1.假设eve对从alice到bob和charlie以及返回给alice的粒子执行攻击(ue，uf)。为了使 此攻击在步骤s4中不会引入错误，eve的最终探测态应独立于alice、bob和
charlie的操作及她们的测 量结果。
[0099]
证明.ue对量子比特|0》和|1》的作用可以表示为
[0100]
ue(|0》|ξ》e)＝β
00
|0》|ξ
00
》+β
01
|1》|ξ
01
》，
ꢀꢀ
(6)
[0101]
ue(|1》|ξe)＝β
10
|0》|ξ
10
》+β
11
|1》|ξ
11
》，
ꢀꢀ
(7)
[0102]
其中|ξ
00
》、|ξ
01
》、|ξ
10
》和|ξ
11
》是依赖于ue的eve的探测态，且|β
00
|2+|β
01
|2＝1，|β
10
|2+|β
11
|2＝1。
[0103]
根据stinespring扩张定理，bob和charlie操作前的复合系统的全局状态为
[0104][0105]
其中下标a、b和c分别表示sa、sb和sc的粒子，并且|e
000
》＝β
002
|ξ
00
》|ξ
00
》，|e
001
》＝β
00
β
01
|ξ
00
》|ξ
01
》， |e
010
》＝β
01
β
00
|ξ
01
》|ξ
00
》，|e
011
》＝β
012
|ξ
01
》|ξ
01
》，|e
100
》＝β
102
|ξ
10
》|ξ
10
》，|e
101
》＝β
10
β
11
|ξ
10
》|ξ
11
》， |e
110
》＝β
11
β
10
|ξ
11
》|ξ
10
》，|e
111
》＝β
112
|ξ
11
》|ξ
11
》。
[0106]
当bob和charlie收到alice发送来的粒子时，他们选择进行sift或ctrl。然后，eve对返回给 alice的粒子施加uf。
[0107]
(i)首先，考虑bob和charlie都选择进行sift的情形。这样，式(8)中的复合系统的状态被 坍塌为|x》a|y》b|z》c|e
xyz
》，其中x，y，z∈{0，1}。为了使eve在步骤s4中不被检测到，bob对原始粒子的 测量结果、charlie对原始粒子的测量结果以及alice对自己手中相应粒子的测量结果都应相同。因此， 可得到
[0108]
|e
001
》＝|e
010
》＝|e
011
》＝|e
100
》＝|e
101
》＝|e
110
》。
ꢀꢀꢀ
(9)
[0109]
而且，alice对来自bob(charlie)的粒子的测量结果应与bob(charlie)制备的新粒子的状态相同，因 此uf应满足
[0110]
uf(|x》a|y》b|z》c|e
xyz
》)＝|x》a|y》b|z》c|f
xyz
》，x＝y＝z∈{0，1}，
ꢀꢀꢀꢀꢀꢀꢀ
(10)
[0111]
意味着uf不能改变bob和charlie的sift操作后的alice、bob和charlie的粒子的状态。否则，eve 将以非零概率被发现。
[0112]
(ii)其次，考虑bob选择进行sift和charlie选择进行ctrl的情形。这样，如果bob的测量 结果为|0》b，式(8)中的复合系统的状态将被坍塌为 |0》a|0》b|0》c|e
000
》+|0》a|0》b|1》c|e
001
》+|1》a|0》b|0》c|e
100
》+|1》a|0》b|1》c|e
101
》；如果bob的测量结果为 |1》b，式(8)中的复合系统的状态将被坍塌为 |0》a|1》b|0》c|e
010
》+|0》a|1》b|1》c|e
011
》+|1》a|1》b|0》c|e
110
》+|
[0131]
为了使eve在步骤s4中不被检测到，alice对bob返回的粒子、charlie返回的相应粒子和她自己 相应粒子的测量结果应处于因此，从式(15)中可以得到
[0132]
|f
000
》＝|f
111
》＝|f》。
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(16)
[0133]
(v)将式(16)插入式(10)中可以得到
[0134]
uf(|x》a|y》b|z》c|e
xyz
》)＝|x》a|y》b|z》c|f》，x＝y＝z∈{0，1}。
ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(17)
[0135]
将式(16)插入式(11)中可以得到
[0136]
uf(|0》a|0》b|0》c|e
000
》+|0》a|0》b|1》c|e
001
》+|1》a|0》b|0》c|e
100
》+|1》a|0》b|1c》c|e
101
》)
[0137]
＝|0》a|0》b|0》c|f》。
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(18)
[0138]
将式(16)插入式(12)可以得到
[0139]
uf(|0》a|1》b|0》c|e
010
》+|0》a|1》b|1》c|e
011
》+|1》a|1》b|0》c|e
110
》+|1》a|1》b|1》c|e
111
》)
[0140]
＝|1》a|1》b|1》c|f》。
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(19)
[0141]
将式(16)插入式(13)可以得到
[0142]
uf(|0》a|0》b|0》c|e
000
》+|0》a|1》b|0》c|e
010
》+|1》a|0》b|0》c|e
100
》+|1》a|1》b|0》c|e
110
》)
[0143]
＝|0》a|0》b|0》c|f》。
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(20)
[0144]
将式(16)插入式(14)中可以得到
[0145]
uf(|0》a|0》b|1》c|e
001
》+|0》a|1》b|1》c|e
011
》+|1》a|0》b|1》c|e
101
》+|1》a|1》b|1》c|e
111
》)
[0146]
＝|1》a|1》b|1》c|f》。
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(21)
[0147]
将式(16)插入式(15)可以得到
[0148][0149]
根据式(17-22)可以得出，为了使这种攻击不在步骤s4引发错误，eve的最终探测态应独立于alice、 bob和charlie的操作及她们的测量结果。
[0150]
应该指出的是，当alice向bob和charlie公布时，eve可能会听到然而，eve仍然无法 从中解密出因为她不知道同样地，当bob(charlie)向charlie(bob)和alice公布(bob)和alice公布时，eve可能会听到然而，eve仍然无法从q
bf
(q
cf
)中解密出因为她不知道因此，eve无法通过发起这种纠缠-测量攻击来获得kf。
[0151]
(3)测量-重发攻击
[0152]
为了知道mb和mc，eve可能截获alice发送的sb和sc的粒子，用z基测量它们并将测得的结果 状态重新发送给bob和charlie。在eve的测量后，alice制备的初态将以相同的概率被坍塌为|000》
abc
或 |111》
abc
。不失一般性，假设alice制备的第j个初态在eve的测量后被坍塌为|000》
abc
。当bob和charlie 都选择进行ctrl时，bob和charlie将接收到的粒子返回给alice；然后alice用ghz基测量来自bob 的粒子、来自charlie的粒子以及她自己手中相应的粒子，并以相同的概率得到或因此，在这种情形下，eve会以的概率被alice、bob和charlie发现。当bob选择进行ctrl且charlie 选择进行sift时，bob将接收到的粒子返回给alice；charlie使用z基测量接收到的粒子以获得测量结 果|0》c，然后制备一个与她发现的状态相同的新粒子并将它发送给alice；alice用z基测量来自bob的 粒子和她自己手中相应的粒子。因此，在这种情形下，eve被alice、bob和charlie检测到的概率为0。 同样地，当bob选择进行sift且charlie选择进行ctrl或者bob和charlie都选择进行sift时，eve 被alice、bob和charlie检测到的概率也为0。综上所述，当eve发起这种测量-重发攻击时，她被检测 到的概率为eve的测量-重发攻击之所以能够被检测到，一方面是因为eve 的测量破坏了初态不同粒子之间的纠缠相关性；另一方面，bob和charlie的操作对于eve来说是随机 的。
[0153]
(4)截获-重发攻击
[0154]
为了知道mb和mc，eve可能事先制备处于z基的假序列截获alice发送的sb(sc) 的粒子，并将的粒子发送给bob(charlie)。不失一般性，这里以的第j个假粒子 为为例。当bob和charlie都选择进行ctrl时，bob和charlie将各自收到的第j个假粒 子返回给alice；alice用ghz基测量来自bob的粒子、来自charlie的粒子和她手上相应的粒子，并以 相同的概率得到或因此，在这种情形下，eve被 alice、bob和charlie检测到的概率为当bob选择进行ctrl且charlie选择进行sift时，bob将 收到的第j个假粒子返回给alice；charlie用z基测量收到的第j个假粒子以获得测量结果制备 一个与她发现的状态相同的新粒子并将它发回给alice；alice用z基测量来自bob的粒子和她自己手中 相应的粒子。因此，在这种情形下，eve被alice、bob和charlie检测到的概率为同样地，当bob 选择进行sift且charlie选择进行ctrl或者bob和charlie都选择进行sift时，eve被alice、bob 和charlie检测到的概率也为综上所述，当eve发起这种截获-重发攻击时，她被检测到的概率为 eve的截获-重发攻击会被发现是由于两个原因：一方面，eve的假粒子 很可能与真实粒子不同；另一方面，bob和charlie的操作对于eve来说是不可预测的。
[0155]
3.2内部攻击
[0156]
2013年，sun等人[32]指出qka方法应具有公平性，即所有参与方对最终共享密钥的贡献相等。 换句话说，参与者的非平凡子集无法确定最终的共享密钥。下面将验证本发明的单态三方sqka方法能 够满足这一要求。
[0157]
在本发明的单态三方sqka方法中，只要alice、bob和charlie在步骤s5之前都忠诚地执行，她 们就可以得到随后用于加密各自的随机密钥。如果他们足够聪明，就没有必要在步 骤s5之前发起攻击。在步骤s5中，alice公布给bob和charlie，bob公布给charlie和alice， charlie公布给alice和bob。因此，他们可能会利用公布加密结果的机会实施欺骗行为。不失一般 性，假设alice不诚实，并且她想单独将最终的共享密钥设置为k
*
。在收到和后，她可以根据来分别解密出和然后，alice计算
[0158][0159]
其中是k
*
中的第r比特，且r＝1,2,
…
,n。然后，alice向bob和charlie公布其中 收到和后，根据bob(charlie)分别解密出 这样，bob(charlie)通过计算得到 假的终钥k
*
。看起来alice的欺骗行为似乎是成功的。然而，在步骤s6中，bob(charlie)计算 的哈希值，发现于是，bob(charlie)拒绝接受k
*
作为最 终共享密钥。因此，alice的欺骗行为失败了。
[0160]
如果两个不忠诚方串通实施类似于上述的欺诈行为，由于哈希函数的使用，他们的欺诈行为也将不 可避免地被第三方发现。
[0161]
现在可以得出结论，由于使用了哈希函数的防碰撞特性[24]，本发明的单态三方sqka方法能够抵 抗内部攻击，具有公平性。
[0162]
实施例：
[0163]
1本发明方法应用举例
[0164]
现在用一个例子来进一步解释密钥协商原理。
[0165]
表示ma中对应info粒子的比特值，，表示mb中对应info粒子的比特值，表示mc对应info粒子的比特值。存在 alice计算其中r＝1,2,
…
,n，并向bob和charlie公布其 中bob计算并向alice和charlie公布其中 charlie计算并向alice和bob公布其中 根据alice从中提取并计算的 哈希值得到结果如果和都成立，alice将接受为最终的共享密钥。bob从和中推导出
并计算计算的哈希值得到结果如果和都成立，bob 将接受为最终的共享密钥。和中推导出并计算的哈希值得到结果如果和都 成立，charlie将接受为最终的共享密钥。如果alice、bob和charlie中的任何一 个拒绝将作为最终共享密钥，通信将被终止并从头开始。
[0166]
2n方sqka方法
[0167]
假设有n(n》3)方p1,p2,
…
,pn，其中p1具有无限的量子能力，而p2,p3,
…
,pn仅具有有限的量子 能力。p1,p2,
…
,pn想要通过量子信道共同协商一个共享密钥，使得各方平等地促成该共享密钥的生成， 也就是该共享密钥不能由她们的任何非平凡子集完全决定。为了实现这一目标，本发明采用n粒子ghz 纠缠态作为量子资源，将上述单态三方sqka方法推广为n方方法，其 步骤具体描述如下。
[0168]
步骤1：p1利用qrng生成原始随机密钥k
1f
，其中同样地，p
t
也使用qrng生成原始随机密钥k
tf
，其中 r＝1,2,
…
,n。然后，p
l
计算她的原始随机密钥k
lf
的哈希值并向其余n-1方公布结果h(k
lf
)。这里， h(k
lf
)表示k
lf
的哈希值，且l＝1,2,
…
,n。
[0169]
步骤2：p1制备2nn个n粒子ghz纠缠态都处于然后，p1将这些n粒子ghz纠缠态 划分为n个序列：其中是s
l
的第j个粒子，l＝1,2,
…
,n，j＝1,2,
…
,2nn。具体 来说，这些ghz纠缠态的所有第l个粒子构成有序序列s
l
。p1逐个将s
t
中的粒子发给p
t
，其中 在p1发送第一个粒子给p
t
后，她只有在收到前一个粒子后才发送下 一个粒子。
[0170]
步骤3：对于接收到的s
t
(t＝2,3,
…
,n)的第j(j＝1,2,
…
,2nn)个粒子，p
t
随机执行以下两个操 作中的一个：
①
ctrl操作，即将第j个接收到的粒子直接无干扰地返回给p1；
②
sift操作，即使用z 基测量第j个接收到的粒子以获得测量结果的比特值制备一个与所发现状态相同的新粒子，并将 它重新发送给p1。p
t
选择进行sift的粒子只有2
n-1
n个。当选择进行sift时，p
t
记下 [0171]
步骤4：p
t
(t＝2,3,
…
,n)告诉p
1 s
t
中她选择进行sift的位置。p1根据p2,p3,
…
,pn的选择对接收 到的粒子执行不同的操作，如表2所示。情形
①
和情形
②
被用于检测s2,s3,
…
,sn的传输是否安全；情形
ꢀ③
不仅用于检测s2,s3,
…
,sn的传输安全性，还用于密钥协商。情形
③
发生的位置有2n个；p1,p2,
…
,pn在 这2n个位置中随机选择n个来检测s2,s3,
…
,sn的传输安全性。
[0172]
在情形
①
中，对于p2,p3,
…
,pn都选择进行ctrl的位置，p1执行操作1。如果不存在
eve，p1的测 量结果应为
[0173]
在情形
②
中，对于不是所有p2,p3,
…
,pn选择进行同样操作的位置，p1执行操作2。如果不存在eve， 选择进行sift的参与方对原始粒子的测量结果、p1对来自选择进行ctrl的参与方的粒子的测量结果 以及p1对自己手中相应粒子的测量结果都应相同；为了检测是否存在eve，选择进行sift的参与方需 告诉p1她们对原始粒子的测量结果；
[0174]
在情形
③
中，对于所有p2,p3,
…
,pn都选择进行sift的位置，p1执行操作3。如果不存在eve， p2,p3,
…
,pn对原始粒子的测量结果和p1对自己手中相应粒子的测量结果应相同；p1对来自p
t
的粒子的 测量结果应该与p
t
制备的新粒子的状态相同；为了检测是否存在eve，p
t
需告诉p1她对选中的n个位置 的测量结果；
[0175]
如果这三种情形中的任何一种错误率异常高，通信将被立即终止；否则，通信将被继续。
[0176]
表2与p2,p3,
…
,pn的操作相对应的p1的操作
[0177][0178]
操作1：p1利用n粒子ghz基测量来自p2,p3,
…
,pn的粒子以及自己手中相应的粒子；
[0179]
操作2：p1利用z基测量来自选择进行ctrl的参与方的粒子和她自己手中相应的粒子；
[0180]
操作3：p1利用z基测量来自p2,p3,
…
,pn的粒子和她自己手中相应的粒子。
[0181]
步骤5：对于情形
③
，在n个用于安全检测的粒子被丢弃后，剩余n个粒子被用于密钥协商。为简 便起见，这些粒子被称为info粒子。p1手上info粒子的测量结果的比特值表示为 表示m
t
中对应于info粒子的比特值，其中 t＝2,3,
…
,n。显然，存在
[0182]m1f
＝m
2f
＝
…
＝m
nf
。
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(24)
[0183]
p
l
计算
[0184][0185]
其中l＝1,2,
…
,n，r＝1,2,
…
,n，并向其余n-1方公布q
lf
，其中
[0186]
步骤6：根据m
lf
，p
l
从q
vf
中提取k
vf
，其中l＝1,2,
…
,n，v＝1,2,
…
,n且v≠l。然后，p
l
计算k
vf
的哈希值得到结果h'(k
vf
)。如果对于v＝1,2,
…
,n且v≠l，有h'(k
vf
)＝h(k
vf
)成立，p
l
将接受 为最终的共享密钥。如果p1,p2,
…
,pn中的任何一个拒绝将 作为最终共享密钥，通信将被终止并从头开始。
[0187]
3讨论与结论
[0188]
在量子通信方法中，通常使用量子比特效率来评估其效率性能，它被定义为
[0189]
[0190]
其中f是最终共享密钥的比特数，q表示消耗的量子比特数，c表示经典通信所需的经典比特数。这里 忽略窃听检测所需的经典资源。在本发明的n方sqka方法中，p1,p2,
…
,pn可以平等确立一个n比特的 最终共享密钥，所以f＝n。p1需要制备2nn个n粒子ghz纠缠态并将s
t
中的粒子逐个发给p
t
；当p
t
选 择对接收到的s
t
的粒子执行sift时，她需要制备2
n-1
n个新的粒子，其中t＝2,3,
…
,n。由此可得出 q＝2nn
×
n+2
n-1n×
(n-1)＝2
n-1
n(3n-1)。p
l
需要向其他n-1方公布h(k
lf
)和q
lf
，其中l＝1,2,
…
,n。 于是可得到c＝mn+nn，其中m是h(k
lf
)的长度。因此，本发明的n方sqka方法的量子比特效率是 [0191]
综上所述，为了实现一个量子方和两个经典方在量子信道上平等地促成共享密钥的生成，本发明设 计了一个新颖的单态三方sqka方法，仅使用一种三粒子ghz纠缠态作为初始量子资源。本发明对其 安全性进行了详细的验证，结果表明它能够抵抗外部攻击和参与者攻击。本发明的单态三方sqka方法 具有以下优点：(1)只采用一种三粒子ghz纠缠态作为初始量子资源；(2)不需要在不同的参与方之 间预先共享密钥；(3)不需要酉操作或量子纠缠交换。最后，通过仅使用一种n粒子ghz纠缠态作为 初始量子资源，本发明将所提出的单态三方sqka方法推广到n方情形，n方方法继承了三方方法的优 良特性。