一种基于散射区模型的室外非视距传播单站定位方法与流程

本发明属于通信技术领域，涉及一种基于散射区模型的室外非视距传播单站定位方法。

背景技术

随着自动驾驶，同步成像，机器人间复杂合作等应用需求的不断增加，未来6G将作为分布式网络提供感知，通信和计算能力，来实现万物感知互连。通】‘’感一体化将在物理和网络世界的融合中发挥至关重要的作用。无线定位作为通感一体化的基础技术之一，受到越来越多的关注。基于卫星的定位系统在山地、深林、城市等复杂地面环境定位精度较低，无法满足现代应用的需求。传统基于测距的无线定位方法中主要假设目标与基站间存在视距传播，但在实际场景中往往不存在视距传播，信号源发射的信号通过散射体散射后到达基站。所接收到的多径信号参数存在非视距偏差，若将其假设为直视路径传播进行定位会严重影响定位精度。现存的指纹定位技术可以在室内非视距环境下进行精确定位，但因为其对定位环境稳定性比较敏感，并且定位场景中需要布置足够的WIFI信号点，导致指纹定位方法并不适用于室外非视距环境定位。因此如何在室外非视距环境中对信号源进行精确定位是当前无线定位面临的关键性问题。

使用多径信号的测距信息对目标进行定位是室外非视距环境下定位目标的常用方法。通过多径信号参数和散射体与目标的空间几何分布，构建定位目标函数。通过优化算法对目标函数求解得到目标位置。然而，此前的定位方法中假设每条多径参数的非视距偏差相同，实际场景中由于传播路径和散射体的分布不同，每条多径的非视距偏差不同，当假设所有多径参数非视距偏差相同时，会严重影响定位精度。此外，大多数定位方法使用多个基站或锚点进行定位，这会消耗更多电力并增加部署成本。与单站相比，使用多站定位需要基站之间的高精度时间同步，这增加了对硬件质量和部署的要求。因此需要研究在室外非视距传播环境下如何使用单基站对信号源进行精确定位。

技术实现要素：

有鉴于此，本发明的目的在于提供一种基于散射区模型的室外非视距传播单站定位方法。首先基于信号传播散射模型，通过多径信号AOA和TOA参数构建伪散射体分布。其次，使用高斯核函数来确定并过滤干扰散射体，并使用K-means聚类算法提取聚类中心。然后使用聚类中心，结合散射体与目标的空间几何分布构建定位目标函数，最后使用基于遗传算法改进的SSA对目标位置进行求解，实现目标在非视距环境下的精确定位。

为达到上述目的，本发明提供如下技术方案：

一种基于散射区模型的室外非视距传播单站定位方法，该方法包括以下步骤：

S1：获取室外非视距传播条件下经过散射体散射到基站的多径信号，构建伪散射体分布；

S2：使用高斯核函数衡量伪散射体分布密度来确定并过滤干扰散射体，使用K-means聚类算法对过滤干扰散射体后的伪散射体进行聚类获得含有定位信息的聚类中心；

S3：结合散射区模型内散射体与目标之间的空间几何结构，使用S2中的聚类中心构建定位目标函数；

S4：针对S3中所提的定位目标函数，使用基于遗传算法改进SSA求解目标位置。

可选的，所述多径信号为AOA和TOA，使用多径信号进行定位；设接收到的第i条多径信号的AOA和TOA参数分别为θi和ti，多径信号传播距离Li＝c×ti，其中c为光速，对应的伪散射体S′i的位置根据多径参数得到，表示为：

x′i＝Li.cos(θi)

y′i＝Li.sin(θi)

引入高斯核函数来衡量两个伪散射体间的距离，设两个伪散射体位置为(x′i,y′i)和(x′j,y′j)，两个伪散射体的高斯核表示为：

可选的，所述干扰散射体的确认过程为：

设置伪散射体的平均高斯核函数作为参考，表示为

其中，dij表示任意两个不相同的伪散射体S′i,S′j的高斯核；AN表示任取两个不相同伪散射体的情况数量，X是所有伪散射体集合；

选取伪散射体S′i,i＝1,2,...,N，其中N为散射体数量；计算该伪散射体与另一伪散射体S′j,j≠i的高斯核dij，将dij与dave比较，若dij≥dave，则S′j是S′i的临近伪散射体；计算所有伪散射体的临近伪散射体数量，s1,s2,...sN；

选取临近伪散射体数量最少的N/5个伪散射体作为干扰散射体，将干扰伪散射体从伪散射体中剔除；

使用K-means聚类算法对去除干扰散射体的伪散射体进行聚类，得到伪散射体的聚类中心其中M为散射区数量。

可选的，所述伪散射体的聚类中心与散射区中心所对应的伪散射体相同；由聚类中心求出目标信号经过对应散射区中心散射到达基站的传播距离L′j和到达角θ′j，表示为：

可选的，所述定位目标函数的求取过程为：

信号经过M个散射区中心散射到达基站的传播距离和到达角分别为L′j,j＝1,2,..,M和θ′j,j＝1,2,...,M；根据空间几何关系，传播距离等于散射区中心到目标(x,y)和基站(xB,yB)的距离和，构建方程组表示为：

设散射区中心到目标的距离为以第M个散射区中心为参考，上述方程组转化为：

由于存在误差，上述方程组没有闭式解，将上述方程组求解过程转化为非线性优化过程，构建误差函数为：

使得所有误差函数的平方和最小的解既是定位目标，定位目标函数表示为：

可选的，所述基于遗传算法改进SSA具体为：

首先，随机构建个体数量为n的种群，并将种群分为领导者和追随者两部分；通过将个体位置带入定位目标函数来获得每个个体的适应度；

领导者通过最优适应度的个体即当前最优解F，迭代改变位置，表示为：

其中F^j表示当前最优解的第j维，用来调整领导者的移动范围，L表示最大迭代次数；c2和c3是[0,1]内的随机值，u^j和b^j表示第j维的上限和下限。

其次，将所述领导者xi,i＝1,2,...,n/2位置进行交叉变异；首先，当变异概率pm大于(0,1)内随机值时，领导者更换为位置上限u＝[u¹,u²,...,u^d]和下限b＝[b¹,b²,...,b^d]内的随机位置，表示为：

其次，当变异概率pc大于(0,1)内随机值时，两个随机的领导者xi,xm在第d′维交叉位置，表示为：

将交叉变异后的领导者与对应的旧领导者进行比较，选取适应度更优的组成新的领导者种群，并选出其中适应度最优的领导者为xbest，第一个追随者的位置通过追随xbest的位置来改变，表示为：

其它追随者的位置根据前一个追随者的位置而迭代表示为：

判断是否到达最大迭代次数，若到达则输出最优适应度的个体F^(L)作为最终解；若未到最大迭代次数则继续更新领导者和追随者的位置。

本发明的有益效果在于：能够使用单基站在非视距传播环境下，充分利用多径信息对信号源进行精确定位。其中考虑了干扰散射体对定位精度的影响，通过高斯核函数过滤干扰散射体来提高定位精度。另外使用改进的SSA-GA来克服求解过程中的局部最优问题。在范围为500×500m的定位场景中，多径参数测量误差在5％的条件下，所提的定位方法的定位误差在20m以内，定位精度相比传统LM方法提高了30m。

本发明的其他优点、目标和特征在某种程度上将在随后的说明书中进行阐述，并且在某种程度上，基于对下文的考察研究对本领域技术人员而言将是显而易见的，或者可以从本发明的实践中得到教导。本发明的目标和其他优点可以通过下面的说明书来实现和获得。

附图说明

为了使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明作优选的详细描述，其中：

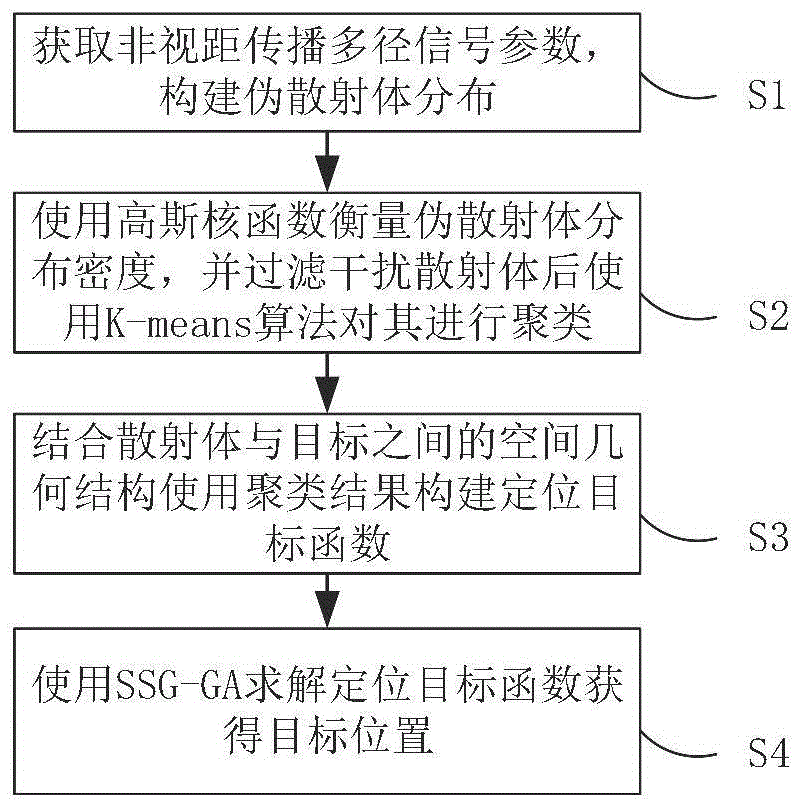
图1为室外非视距传播环境下单站定位方法流程图；

图2为SSA-GA流程图；

图3为散射区示意图；

图4为伪散射体分布示意图；

图5为过滤和未过滤干扰散射体情况下的伪散射体聚类结果；图5(a)为过滤干扰散射体的聚类结果；图5(b)为未过滤干扰散射体的聚类结果；

图6为过滤和未过滤干扰散射体情况下的伪散射体聚类中心误差；

图7为过滤和未过滤干扰散射体情况下的目标定位误差；

图8为分别使用三种算法对目标进行定位的定位误差；图8(a)为SSA算法；图8(b)为SSA-GA算法；图8(c)为LM算法；

图9为SSA-GA，SSA和LM算法的定位误差累计分布曲线；

图10为多径测量误差从3％增长到12％时，本发明所提的定位方法的定位误差。

具体实施方式

以下通过特定的具体实例说明本发明的实施方式，本领域技术人员可由本说明书所揭露的内容轻易地了解本发明的其他优点与功效。本发明还可以通过另外不同的具体实施方式加以实施或应用，本说明书中的各项细节也可以基于不同观点与应用，在没有背离本发明的精神下进行各种修饰或改变。需要说明的是，以下实施例中所提供的图示仅以示意方式说明本发明的基本构想，在不冲突的情况下，以下实施例及实施例中的特征可以相互组合。

其中，附图仅用于示例性说明，表示的仅是示意图，而非实物图，不能理解为对本发明的限制；为了更好地说明本发明的实施例，附图某些部件会有省略、放大或缩小，并不代表实际产品的尺寸；对本领域技术人员来说，附图中某些公知结构及其说明可能省略是可以理解的。

本发明实施例的附图中相同或相似的标号对应相同或相似的部件；在本发明的描述中，需要理解的是，若有术语“上”、“下”、“左”、“右”、“前”、“后”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此附图中描述位置关系的用语仅用于示例性说明，不能理解为对本发明的限制，对于本领域的普通技术人员而言，可以根据具体情况理解上述术语的具体含义。

请参阅图1，为一种基于散射区模型的室外非视距传播单站定位方法，包括以下步骤：

基站测得第i条多径信号的AOA和TOA参数分别为θi和ti，多径信号的传播距离Li＝c×ti。根据几何结构伪散射体S′i位置可由多径参数表示为：

x′i＝Li.cos(θi)

y′i＝Li.sin(θi)

NLOS环境下，每条多径对应一个伪散射体，也对应一个实际散射体，在障碍物体密集的定位区域之中，散射体在散射区内的分布呈现聚集式分布，所以多径对应的伪散射体也有类似的分布特性，对于呈聚集式分布的特性的数据而言，可以用聚类算法对其进行处理提取有用数据。由于散射区外干扰散射体的影响，在使用K-means聚类算法对其进行聚类时会有较大偏差。因此需要进一步的对伪散射体进行过滤，使用高斯核函数来衡量两个伪散射体(x′i,y′i)和(x′j,y′j)的距离，表示为：

其中，σ表示高斯核宽度参数。

进一步的，为了区分干扰散射体，设置所有伪散射体与其它伪散射体高斯核的平均值为参考高斯核函数dave，表示为：

其中，dij表示的任意两个不相同的伪散射体S′i,S′j间的高斯核。AN表示所有伪散射体中取出两个的所有情况，X是所有伪散射体集合。

其次，若两个伪散射体的高斯核大于参考高斯核，则这两个伪散射体互为临近散射体。计算所有伪散射体的临近散射体数量为s1,s2,...sN。选择临近散射体数量最小散射体作为干扰散射体进行滤除。过滤实现过程如表1所示。

表1干扰散射体过滤实现过程

进一步的，使用K-means算法对滤除干扰散射体后的伪散射体进行聚类，获得聚类中心由于伪散射体与相对应的散射体分布同样具有聚集性，伪散射体的聚类中心等于散射区中心所对应的伪散射体。因此信号经过散射区中心散射到达基站的多径信号传播距离L′i和到达角θ′i可由聚类中心表示为

进一步的，根据散射体与目标空间几何结构，信号传播距离等于信号从基站到散射体的距离与信号从目标到散射体的距离和。由此结合聚类中心所对应的多径参数可构建方程组

其中实际散射区中心位置和基站位置(xB,yB)已知。设目标到每个散射区中心的距离为lj，表示为

以第M个散射中心为参考，不同散射区中心和第M个散射中心到目标的距离差可以表示为

在实际场景中，由于存在测量误差，目标的位置没有闭式解，因此求解过程需要转化为非线性优化问题，我们将目标方程重写为一组误差函数为：

通过对每个散射中心对应的定位误差函数值最小二乘，就能求出目标位置(x,y)。因此定位目标函数为：

对于上述非线性优化问题，通过遗传算法对SSA进行改进提出SSA-GA求解目标位置。首先构建个体数量为n的种群，并将种群分为领导者和追随者两部分。通过将个体带入定位目标函数来获得每个个体的适应度。领导者通过最优适应度的个体即当前最优解F迭代改变位置，表示为：

其中Fj表示当前最优解的第j维，用来调整领导者的移动范围，L表示最大迭代次数。c2和c3是[0,1]内的随机值，uj和bj表示个体在第j维的上限和下限。

进一步的，领导者位置经过交叉变异来扩大全局搜索性，当变异概率pm大于(0,1)内随机值时，领导者位置更新为上下限内的随机位置，表示为：

其次，当变异概率pc大于(0,1)内随机值时，两个随机的领导者xi,xm在第d′维交叉位置，表示为：

进一步的，比较交叉变异后的领导者和原种群中领导者的适应度，更新领导者种群，并选取适应度最优的领导者xbest，用来更新第一个追随者的位置，表示为：

其它追随者的位置通过前一个追随者的位置而迭代改变，表示为：

若迭代次数为达到最大迭代次数L，则结束迭代输出最优适应度的个体作为最终解，否则继续更新领导者和追随者的位置。SSA-GA算法增强了全局搜索能力，降低了局部最优情况的发生，提高了定位精度，如图2所示。算法实现过程如表2所示。

表2 SSA-GA算法

本发明针对于室外非视距环境下单站定位问题，提供一种基于散射区模型的室外非视距单站定位方法。步骤包括：S1、获取室外非视距传播条件下信号源信号经过散射体散射到基站的多径信号参数，结合空间几何结构构建伪散射体分布；S2、使用高斯核函数判断伪散射体分布密度确定并过滤干扰散射体并用K-means聚类算法对过滤干扰散射体后的伪散射体进行聚类得到含有定位信息的聚类中心；S3、结合散射体与目标之间的空间几何结构，使用S2中的聚类中心构建定位目标函数；S4、针对S3中所提的定位目标函数使用基于遗传算法的改进SSA求解目标位置。

通过仿真设定信号源与散射区域分布，散射体区域分布如图3所示，来自信号源的信号经过散射区内散射体S1,S2,...,SN散射后到达基站。在本实例中设置定位区域范围为500(m)×500(m)，散射区数量M＝3。基站位置为(0,0)待求目标坐标为(400,200)，散射区中心坐标为(500,100)(300,300)和(400,350)。基站测量到的多径信号的AOA和TOA参数分别为θi和ti，其伪散射体坐标可根据多径参数得到表示为：

x′i＝Li.cos(θi)

y′i＝Li.sin(θi)

通过过滤干扰散射体并使用K-means算法进行聚类后，得到的聚类中心为将聚类中心转化为经过散射区中心散射到基站的多径信号的AOA和TOA相关参数，表示为：

结合空间几何结构，由聚类中心所对应多径参数可构建方程组表示为

将目标方程重写为一组误差目标函数为

通过每个散射中心对应的定位误差函数值最小二乘，就能求出目标位置(x,y)。因此定位目标函数表示为

根据仿真定位场景，分析比较过滤干扰散射体，优化算法和散射区参数对本发明定位性能的影响。首先对比未过滤干扰散射体和过滤干扰散射体对定位的影响，其次对比传统SSA,LM算法与本发明所提SSA-GA的定位精度，进一步说明本方法具有较高的定位精度，最后对比不同的散射区参数和多径测量误差下的定位结果，研究环境参数对本方法定位精度的影响。图4为伪散射体分布示意图。过滤和未过滤干扰散射体的聚类结果如图5所示，当仿真参数相同时，通过过滤干扰散射体，散射区外的散射体被明显滤除了，散射区内散射体分布更具有聚集性。图6和图7分别为过滤和未过滤干扰散射体的聚类中心误差和定位误差，可以看出相比于未过滤干扰散射体，过滤干扰散射体后的聚类中心误差和定位误差更低，尤其是随着干扰散射体数量的增多，聚类中心误差和定位误差受干扰散射体的影响更为明显，未过滤干扰散射体时，聚类误差和定位误差随干扰散射体增多明显升高，过滤干扰散射体后的聚类误差和定位误差受到干扰散射体数量增多的影响较小。进一步，图8，图9分别给出了3种优化算法的定位误差和定位误差累计分布，图8(a)为SSA算法；图8(b)为SSA-GA算法；图8(c)为LM算法；从图中可以看出，无论哪种优化算法，定位误差都受到散射区半径和散射体数量的影响。其中散射区半径越大定位误差越高，散射体数量越多定位精度越高，这说明散射体的分布越具有聚集性，聚类中心误差越低，定位精度越高。图10给出了定位误差随多径参数测量误差增加的变化趋势。结果表明随着多径参数测量误差的增加，定位误差明显增大，特别的定位误差随TOA测量误差增加的变化更大。说明在构建伪散射体分布和定位目标函数时都使用了多径TOA参数，使得本方法的定位精度受到TOA测量误差影响更大。

最后说明的是，以上实施例仅用以说明本发明的技术方案而非限制，尽管参照较佳实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，可以对本发明的技术方案进行修改或者等同替换，而不脱离本技术方案的宗旨和范围，其均应涵盖在本发明的权利要求范围当中。