基于共生NOMA系统安全性能设计方法

基于共生noma系统安全性能设计方法
技术领域
1.本发明涉及共生无线电技术领域，具体地，涉及一种基于共生noma系统安全性能设计方法。


背景技术：

2.非正交多址(non-orthogonal multiple access，noma)技术是第五代(5th generation，5g)蜂窝网络的关键技术创新之一，有可能实现高效频谱效率。
3.5g的大规模机器通信服务类别支持低功耗、低数据需求的超密集部署连接设备，因此它支持物联网通信。此外，共生无线电(symbiotic radio，sr)技术利用了环境反向散射通信低能量需求的特点，具有实现能量受限的物联网通信的潜力。


技术实现要素：

4.针对现有技术中的缺陷，本发明的目的是提供一种基于共生noma系统安全性能设计方法。本发明为提高通信系统的安全性能且使用有限的频谱得到高效利用，将非正交多址技术与共生无线电相结合，在共生noma网络中采用了人工噪声技术，推导网络的安全中断概率和安全中断概率来研究系统的安全中断性能，同时采用了连续hopfield神经网络来寻求最优的人工噪声分配因子以达到系统性能最优。
5.根据本发明提供的基于共生noma系统安全性能设计方法，包括如下步骤：
6.步骤s1：构建共生noma系统模型，该模型包括主发射机pt，反向散射装备bd以及主接收机pr，其中窃听用户e试图截获pt和bd的信号；
7.步骤s2：控制pt将机密信息和干扰信息混合叠加形成发送信号，并将所述发送信号发送出；
8.步骤s3：bd反向散射对所述发送信号接收生成的接收信号，并将信息c(t)调制到接收信号上之后，向pr发送；
9.步骤s4：bd根据放大因子将接收信号进行放大；
10.步骤s5：推导pr和bd的安全中断概率以及安全容量；
11.步骤s6：优化机密信息和干扰信息分配因子，以使所述中断概率最小化。
12.优选地，在步骤s2中pt处的发送信号为：
[0013][0014]
其中，x1(t)表示要发送给pr的机密信息，x2(t)表示要发送给pr用来抵御窃听的干扰信息；p表示pt处的总发送功率；a1和a2分别表示x1(t)和x2(t)的功率分配系数，a1+a2＝1。
[0015]
优选地，所述干扰信息是一个预设的伪随机信号并且提前存储在pr处用于干扰抵消。
[0016]
优选地，此时，pr和e接收到的信号分别表示为：
[0017]
[0018][0019]
其中，n
pr
,ne～cn(0,σ2)分别表示各节点处的加性高斯白噪声，σ2表示方差；h
pr
为pt与pr之间的信道增益，η为bd的反射系数，h
pb
为pt与bd之间的信道增益，h
br
为bd与pr之间的信道增益，h
pe
为pt与窃听用户e之间的信道增益，h
be
为bd与窃听用户e之间的信道增益；
[0020]
在pr处可以分辨出干扰信号并去除，但窃听用户e只能将干扰信号当作背景噪声处理，pr和e解码x1(t)的信噪比和信干燥比分别为：
[0021][0022][0023]
其中，表示pt处的发射信噪比。
[0024]
优选地，所述放大因子g为：
[0025][0026]
其中，pb表示bd处的发射功率。
[0027]
优选地，步骤s4中，pr和窃听用户e收到的信号分别为：
[0028][0029][0030]
此时，pr和e在解码x1(t)的sinr为：
[0031][0032][0033]
其中，表示bd处的发射信噪比。
[0034]
优选地，步骤s6具体为：当pr端未成功解码x1(t)，发生中断；
[0035]
首先根据信噪比得到pr在2个时隙的安全容量首先根据信噪比得到pr在2个时隙的安全容量分别为
[0036][0037][0038]
其中，lb为以2为低的对数即log2。
[0039]
利用选择合并技术来输出信号，此时pr的安全中断概率p
pr
为
[0040][0041]
其中，r
pr
表示pr的目标速率，pr表示为概率，为pr在第1个时隙的安全容量，为pr在第2个时隙的安全容量。
[0042]
ω1,ω2的表达式为
[0043][0044][0045]
式(14)中χ(.)为
[0046][0047][0048]
其中，l表示复杂度-精确度平衡参数；l为变量参数；
[0049]
根据noma协议，可得到bd的中断概率δ为
[0050]
δ＝pr{c
bd
＜r
bd
}
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(18)
[0051]
其中，r
bd
表示bd的目标速率，c
bd
为bd处的安全容量。
[0052]
优选地，在步骤s6中利用连续hopfield神经网络优化优化机密信息和干扰信息分配因子。
[0053]
与现有技术相比，本发明具有如下的有益效果：
[0054]
本发明在共生noma系统中，采用人工噪声技术的情况下，推导出网络的安全中断概率和安全吞吐量，此外采用连续hopfield神经网络来寻求最优的人工噪声分配因子，提高了通信系统的安全性能且使用有限的频谱得到高效利用。
附图说明
[0055]
通过阅读参照以下附图对非限制性实施例所作的详细描述，本发明的其它特征、目的和优点将会变得更明显：
[0056]
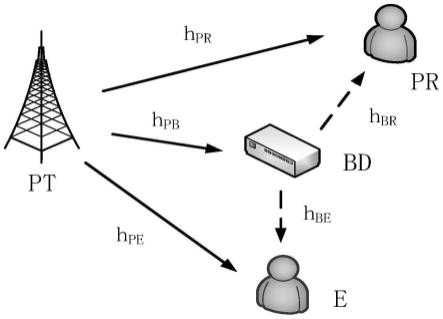
图1为本发明实施例中共生noma系统模型的示意图；
[0057]
图2为本发明实施例中基于共生noma系统安全性能设计方法的步骤流程示意图。
具体实施方式
[0058]
下面结合具体实施例对本发明进行详细说明。以下实施例将有助于本领域的技术人员进一步理解本发明，但不以任何形式限制本发明。应当指出的是，对本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变形和改进。这些都属于本发明的保护范围。
[0059]
图1为本发明实施例中共生noma系统模型的示意图，如图1所示，该模型包括主发射机(primary transmitter，pt)，反向散射装备(backscatter device，bd)和主接收机(primary receiver，pr)。其中窃听用户(eavesdropper，e)试图截获主发射机和反向散射装备的信号。
[0060]
在该共生noma系统模型中，采取人工噪声技术来提高安全性能。链路pt-pr、pt-bd、pt-e、bd-pr、bd-e的信道增益表示为i∈{pr,pb,pe,br,be}。假设所有的信道增益均服从均值为0、方差为的瑞利分布且相互独立。
[0061]
步骤3：pt将机密信息和干扰信息混合叠加发送，此时记pt处的发送信号为：
[0062][0063]
其中，x1(t)表示要发送给pr的机密信息，x2(t)表示要发送给pr用来抵御窃听的干扰信息，该干扰信息是一个预设的伪随机信号并且提前存储在pr处用于干扰抵消；p表示pt处的总发送功率；a1和a2分别表示x1(t)和x2(t)的功率分配系数，a1+a2＝1。
[0064]
步骤4.bd反向散射其接收到的信号，将自己的信息c(t)调制到接收信号上之后，向pr发送。
[0065]
bd的信息信号被建模，e[|c(t)|2]＝1，其中e[.]表示统计量的期望操作。bd反射回来的那部分接收功率由反射系数η∈[0,1]建模，即(1-η)p代表适用于负载调制方案的功率，改变了不同状态之间的阻抗，其中ηp代表反向散射功率。此时，pr和e接收到的信号分别表示为：
[0066][0067][0068]
其中，n
pr
,ne～cn(0,σ2)分别表示各节点处的加性高斯白噪声，σ2表示方差。在pr处可以分辨出干扰信号并去除，但窃听用户只能将干扰信号当作背景噪声处理，pr和e解码x1(t)的信噪比(signal-to-noise radio,snr)和信干燥比(signal-to-interference-noise radio,sinr)分别为：
[0069][0070][0071]
其中，表示pt处的发射信噪比。
[0072]
步骤5.bd可利用af技术将重叠信号进行放大，放大因子为
[0073][0074]
其中，pb表示bd处的发射功率。此时，pr和e收到的信号分别为
[0075]
[0076][0077]
此时，pr和e在解码x1(t)的sinr为：
[0078][0079][0080]
其中，表示bd处的发射信噪比。
[0081]
步骤6.推导pr和bd的安全中断概率以及安全容量。根据noma协议，当pr端未成功解码x1，发生中断。首先根据信噪比得到pr在2个时隙的安全容量分别为
[0082][0083][0084]
利用选择合并技术来输出信号，此时pr的安全中断概率为
[0085][0086]
其中，r
pr
表示pr的目标速率，ω1,ω2的表达式为
[0087][0088][0089]
式(14)中χ(.)为
[0090][0091][0092]
其中，l表示复杂度-精确度平衡参数。
[0093]
根据noma协议，可得到bd的中断概率为
[0094]
δ＝pr{c
bd
＜r
bd
}
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(18)
[0095]
其中，r
bd
表示bd的目标速率。
[0096]
步骤6.利用连续hopfield神经网络优化人工噪声分配因子，达到中断概率最小化。hopfield是一种利用模拟电路实现对网络的神经元描述。假设神经元j(j＝1,2,
…
,n)的内部膜电位状态用ui表示。其中，rj和cj的并联模拟了生物神经元的时间常数，w
ij
模拟了神经元间的突触特性，运算放大器模拟了神经元的非线性特征，ij相当于阈值。由基尔霍夫电流定律可知：
[0097][0098]
式中，n为神经网络神经元的个数；vj(t)为输出电位；uj(t)为输入电位；gj为神经元的传递函数；w＝w
ij
(i,j＝1,2,
…
,n)为网络权系数矩阵。rj为传递电阻，cj为输入电容。
[0099]
在实际应用中，将最优化问题的目标函数转换成连续hopfield神经网络的能量函数，把问题的变量对应于网络中神经元的状态，那么hopfield神经网络就能够用于解决优化组合问题。即当网络的神经元状态趋于平衡点时，网络的能量函数也趋于最小值，网络由初态向稳态收敛的过程就是目标函数优化计算的过程。由于神经网络是并行计算的，其计算量不会随着维数的增加而发生指数性“爆炸”，因而对于优化问题的高速计算效率高。令ω＝{s1,s2,
…
,sn}为所有状态构成的解空间，c(si)为状态si对应的目标函数值，要求寻找最优解s*，使得对于所有的si∈ω，有c(s*)＝min(c(si))。
[0100]
首先网络输入初始化：
[0101]uxi
(t)＝u0ln(n-1)+δ
xi (xi＝1,2,
…
,n；t＝0)
ꢀꢀꢀꢀꢀꢀꢀꢀ
(15)
[0102]
式中，u0＝0.1，δ
xi
为(-1,+1)区间的随机值。t表示时间，u
xi
(t)为输入电位，n为参数变量。
[0103]
采样时间设置为step＝0.0001，迭代次数为10000。
[0104]
步骤7.构造网络能量函数和动态方程。网络的能量函数包含目标项和约束项两部分，将网络的能量函数定义为：
[0105][0106]
式中，前两项为问题的约束项；第三项为待优化的目标项，取a＝200，d＝100，n为参数变量，v
xi
和v
y,i+1
均为输出电位。
[0107]
动态方程为：
[0108][0109]
计算并利用一阶欧拉法计算得到：
[0110][0111]
其中，u
xi
为输入电位，δt为t+1时刻与t时刻电位差
[0112]
步骤8.判断迭代次数是否结束，若迭代次数k》10000，则终止，否则k＝k+1，返回步骤7。
[0113]
以上对本发明的具体实施例进行了描述。需要理解的是，本发明并不局限于上述特定实施方式，本领域技术人员可以在权利要求的范围内做出各种变形或修改，这并不影响本发明的实质内容。