一种逼近信道容量的低PAPR星座图设计方法

一种逼近信道容量的低papr星座图设计方法
技术领域
1.本发明属于通信信号传输技术领域，具体涉及在加性高斯白噪声信道下，逼近信道容量的低papr星座图的设计，是一种有效性更高、实用性更广的星座成形方法。


背景技术：

2.通信技术的疾速发展促使用户对通信质量的需求持续增加，大量已有或正在发展的通信业务如超高清视频传输、无人驾驶、全息通信等对通信速率提出了极高的要求。为适应高速传输的业务需求，一方面，可以通过使用更高频段的信号进行通信(如太赫兹通信)以获得更宽的带宽，或采用大规模mimo等技术提升可达的传输速率；另一方面，可从发送信号的设计入手，研究更加逼近信道容量的星座图方案。值得一提的是，两方面技术可以结合使用，能极大地提高可达的传输速率，本发明主要涉及后一个方面。
3.传统的正交幅度调制(quadrature amplitude modulation,qam)在无差错传输的前提下，可达到的最大传输速率与信道容量存在一定的差距，为了消除这个差距，发展出了几何成形和概率成形两类技术，如kschischang提出了一种基于maxwell-boltzmann分布的概率成形方法，betts基于几何成形提出了一种非均匀qam星座图等。最近，考虑到通信系统通常使用等概星座点的情况，大部分文献聚焦于研究几何成形技术，meric利用box-muller变换将两组均匀排列的点集转化为二维高斯形状，在此基础上提出了逼近信道容量的振幅相移键控(amplitude and phase-shift keying,apsk)星座图，larsson仿照自然界中向日葵种子等的排布规则，提出了一种黄金角度调制(golden angle modulation,gam)方法，该方法的可达传输速率随星座点数增加相比于apsk能更快地收敛到信道容量，但是其峰均功率比(peak-to-average power ratio,papr)较高，且星座点的幅度种类较多，不利于在非线性信道中传输。


技术实现要素：

4.本发明提出了一种逼近信道容量的低papr星座图设计方法，旨在解决gam调制papr较高、星座点的幅度种类较多，从而导致的非线性信道适应性弱的问题，以及解决apsk调制在星座点数较小时，可达传输速率与信道容量差值较高的问题。
5.一种逼近信道容量的低papr星座图设计方法，包括如下步骤：
6.步骤1)首先推导出逼近信道容量的星座图幅度和相位的联合分布，即利用二维高斯分布的极坐标形式得到逼近信道容量的星座图幅度和相位的联合分布函数；
7.步骤2)使用星座图幅度和相位的联合分布求得星座图相位的边缘分布函数，基于黄金角度设计出星座点的相位，若星座点数为n，则相位设置成2πρn，n＝1,l,n，其中
8.步骤3)利用星座图幅度和相位的联合分布得出星座图幅度的边缘分布函数，基于逆变换采样法(inverse transform sampling)设计出星座点的幅度为其中
k＝1,l,q；
9.步骤4)对于papr受限的情形，基于截断高斯分布得到星座图幅度边缘分布函数的修正形式，若考虑使用均值为0、方差为p/2、范围在(-a,a)的截断高斯分布，基于逆变换采样法设计出低papr星座图的修正幅度为样法设计出低papr星座图的修正幅度为k'＝1,l,q。
10.本发明利用二维高斯分布的极坐标形式推导出逼近信道容量的星座图幅度和相位的边缘分布函数，尔后基于黄金角度获得星座图相位的设计方案，以及基于逆变换采样法(inverse transform sampling)得到星座图幅度的设计方案，另外，基于截断高斯分布对已得到的星座图幅度进行修正，从而获得papr更低的星座图。仿真实验表明，提出的星座图较之于gam有更少的幅度种类，且未修正前的星座图可达传输速率随着星座点数的增加相比于gam、apsk能更快的收敛至信道容量，修正后的星座图尤其在星座点数较大时能以较少的可达传输速率性能来换取papr的大幅度降低。
附图说明
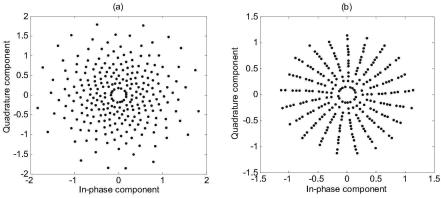
11.图1是n＝256时采用本发明的低papr星座图设计方法得到的星座图：其中(a)是无papr约束条件下得到的星座图，(b)是低papr约束条件下得到的星座图。
12.图2是snr＝10db时可达到的最大传输速率与信道容量的差值随q的变化曲线图。
13.图3是snr＝18db时可达到的最大传输速率与信道容量的差值随q的变化曲线图。
14.图4是q＝20时可达到的最大传输速率随snr的变化曲线图。
15.图5是snr＝8db时papr随q的变化曲线图。
具体实施方式
16.下面结合附图对本发明的技术方案进行详细描述：
17.本发明的逼近信道容量的低papr星座图设计方法，应用的通信场景主要针对的是加性高斯白噪声(additive white gaussian noise，awgn)信道，设发送信号为s(t)，噪声信号为n(t)，接收信号为r(t)，则
18.r(t)＝s(t)+n(t)
ꢀꢀꢀ
(1)
19.其中发送信号s(t)的平均功率约束为p，噪声功率为n0，这里p/n0即为awgn信道的信噪比，记作snr＝p/n0。此时，信道容量为
[0020][0021]
当s(t)是均值为零，方差为p的高斯信号时，awgn信道无差错传输的最大传输速率可以达到信道容量，显然这时s(t)为连续波形信号。
[0022]
在数字通信系统中，发送信号选自有限的星座点，不再是连续波形信号，因而可达到的最大传输速率与信道容量必然存在一定的差距，如何最大限度的减小这种差距是一个富有挑战性的问题。
[0023]
本发明提出一种逼近信道容量的低papr星座图设计方法，包括以下步骤：
[0024]
步骤1)首先推导出逼近信道容量的星座图幅度和相位的联合分布，即利用二维高斯分布的极坐标形式得到逼近信道容量的星座图幅度和相位的联合分布函数；
[0025]
设星座点数为n，发送信号选择各个星座点的概率(记作pn，n＝1,l,n)相同，即pn＝1/n。由上文可知，发送信号在一个维度上服从高斯分布时，该信道可达到的最大传输速率由式(2)给出，若考虑二维星座图时，发送信号存在两个维度，此时有s(t)＝sr(t)+i
·
si(t)，其中sr(t)和si(t)分别为发送信号s(t)的实部和虚部。对于二维发送信号，若在每一维上的信号(即sr(t)和si(t))均服从均值为零、方差为p/2的高斯分布，则此信道可达到的最大传输速率为2c，亦是二维情况下信息无差错传输的最大速率，这时sr(t)和si(t)信号的概率密度函数分别为
[0026][0027]
由于两个维度的分量之间统计独立，所以其联合概率密度为
[0028][0029]
将上式转换为极坐标形式，令x＝rcosθ，y＝rsinθ，则有
[0030][0031]
其中r、θ分别为星座点的幅度和相位。
[0032]
步骤2)使用星座图幅度和相位的联合分布求得星座图相位的边缘分布函数，基于黄金角度设计出星座点的相位，若星座点数为n，则相位设置成2πρn，n＝1,l,n，其中常数
[0033]
计算相位θ的边缘分布函数如下
[0034][0035]
由此可见，信息无差错传输的最大速率达到2c时，相位满足在(0,2π)上服从均匀分布，即后者是前者的必要条件。
[0036]
对于数字通信系统，发送信号的相位为有限种(即n种)，为使得可达到的最大传输速率更接近于2c，需使n种相位更趋于(0,2π)的均匀分布。值得一提的是，基于box-muller变换的apsk星座图的相位仅有种，随着n的增加，其相位虽然逐渐趋于均匀分布，但收敛速度较慢。为了加快收敛速度，采用基于黄金角度的相位设计方法，将n个星座点的相位设置成2πρn，n＝1,l,n，其中该角度也是自然界中向日葵种子等的排布角度，业已证明采用黄金角度排布的方式可使得植物的每个分枝在一个圆周上趋于均匀分布，因此，n个星座点按照黄金角度排布能保证相应的n个相位趋于(0,2π)的均匀分布。
[0037]
步骤3)利用星座图幅度和相位的联合分布得出星座图幅度的边缘分布函数，基于
逆变换采样法(inverse transform sampling)设计出星座点的幅度为其中k＝1,l,q；
[0038]
对于式(5)，计算幅度r的边缘分布函数如下
[0039][0040]
设u服从(0,1)上的均匀分布，根据逆变换采样法，则服从式(7)给出的分布，其中为fr(
·
)的反函数，可写为
[0041][0042]
由于1-u亦服从(0,1)上的均匀分布，因而可将上式中1-u替换成u，即服从式(7)给出的分布。结合上文推导可知，幅度r服从式(7)给出的分布是信息无差错传输的最大速率达到2c的必要条件，而满足此条件的幅度r可由给出。
[0043]
假设为整数，定义集合显然该集合中的元素在(0,1)内等间隔均匀排列，设令则r1,l,rk在几何形状上近似呈式(7)给出的分布。
[0044]
结合上述相位和幅度的设计方案，相应星座点组成矩阵x，其元素为
[0045][0046]
其中[x]
kq
表示矩阵x的第k行q列元素，q＝1,l,q。可以看出x为q
×
q矩阵，即共有n个元素，这些元素对应n个星座点。
[0047]
下面证明由式(9)给出的星座点满足发送信号平均功率为p的约束，计算由式(9)给出的星座点的平均功率为
[0048][0049]
由分部积分可得
[0050][0051]
易证对于j≥1/2成立，代入上式，可得
[0052][0053]
所以有
[0054][0055]
将式(13)代入到式(10)得到p
x
≤p，可见，由式(9)给出的星座点满足发送信号平均功率为p的约束。
[0056]
步骤4)对于papr受限的情形，基于截断高斯分布得到星座图幅度边缘分布函数的修正形式，若考虑使用均值为0、方差为p/2、范围在(-a,a)的截断高斯分布，基于逆变换采样法设计出低papr星座图的修正幅度为样法设计出低papr星座图的修正幅度为k'＝1,l,q；
[0057]
按式(9)设计出的星座图，当星座点数增大时，由于其相位和幅度分别趋近于式(6)和式(7)，所以其理论传输速率可逼近信道容量。然而，上述设计过程并没有考虑实际应用中可能出现的papr受限的问题，为了进一步降低上文提出的星座图的papr，采用基于截断高斯分布的方案进行设计。
[0058]
设sr(t)和si(t)均服从(-a,a)的截断高斯分布，其均值为零，方差为p/2，则其概率密度函数分别为
[0059][0060]
其中-a≤x≤a，-a≤y≤a。
[0061]
此时，sr(t)和si(t)的联合概率密度为
[0062][0063]
将上式转换为极坐标形式，令x＝rcosθ，y＝rsinθ，则有
[0064][0065]
其中则幅度r的边缘分布函数计算如下
[0066][0067]
由逆变换采样法可知，服从式(17)的随机变量可写为其中ξ服从(0,1)上的均匀分布。设k'＝1,l,q，令则l,在几何形状上近似呈式(17)给出的分布。
[0068]
以上为低papr星座图幅度设计方案，其相位设计同样采用基于黄金角度的方法，即n个星座点的相位设置成2πρn，n＝1,l,n。综上，设n个星座点组成矩阵y，其第k'行q'列元素为
[0069][0070]
由c的表达式可知，c》1，则另外，容易得出，当k'＝1,l,q时，利用式形成的集合与相同，所以采用这两者作为幅度设计出的星座图具有相同的平均功率，都等于p
x
。可以推断出，由式(18)给出的星座点的平均功率(记作py)比p
x
小，即py《p
x
。前文已证明使用作为星座点幅度时，其平均功率p
x
≤p。综合上述分析可得py《p
x
≤p，可见，由式(18)给出的星座点满足发送信号平均功率为p的约束。
[0071]
以上是本发明提出的一种逼近信道容量的低papr星座图设计方法的详细实施步骤，下面通过仿真实验来验证本方法的有效性和可靠性。
[0072]
设置发送信号平均功率p＝1，图1给出了当n＝256时提出方案的星座图，其中图(a)为提出的星座图(无papr约束)，即式(9)给出的星座图；图(b)为提出的星座图(低papr)，即式(18)给出的星座图，这里a＝1.5。由图1可以看出，提出星座图的幅度种类仅有16种(即种)，而gam星座图幅度种类有n种，所以提出星座图的幅度种类数更少，另外，提出的低papr星座图相应的星座点横纵坐标均在(-1.5,1.5)范围内，其峰值功率受限。
[0073]
提出的星座图其可达到的最大传输速率与信道容量的差值(capacity gap)随gap)随变化的曲线如图2和图3所示，其中，图2中信噪比snr＝10db，图3中信噪比snr＝18db，为方便叙述，将“可达到的最大传输速率与信道容量的差值”简记为“容量差值”。
[0074]
从图2中可以看到，提出星座图的容量差值在星座点数增加时逐渐趋近于零，当q《4时，提出星座图的容量差值略比qam高，当q》4时，提出星座图的容量差值低于qam，且随着星座点数增加，提出星座图的容量差值性能较之于qam的优势越明显。另外，gam和apsk的容量差值亦随着星座点数的增加而趋近于零，但是两者的收敛速度均比提出的星座图(无papr约束)慢，具体来说，gam容量差值的收敛速度略慢于提出的星座图(无papr约束)，而
apsk容量差值的收敛速度则明显慢于提出的星座图(无papr约束)。提出星座图(低papr)的容量差值同样具有较快的收敛速度，但当q增加时，其容量差值性能介于qam和gam之间，这是由于提出星座图(低papr)基于的是截断高斯分布，即在容量差值与papr性能之间进行了折衷。
[0075]
由图3可知，当q＝4，5，6或7时，提出星座图的容量差值性能略差于qam，而当q》9时，提出星座图相比于qam具有更低的容量差值，且随着星座点数的增加，性能差距愈加明显。同时，对比图2与图3可知，提出星座图与qam容量差值曲线的交点随着信噪比的增加向右偏移。gam、apsk与提出星座图的容量差值曲线之间的关系和图2相似，且在星座点数较多时(如q＝20时，即n＝400)，提出星座图(无papr约束)的容量差值亦明显小于其他星座图，而提出星座图(低papr)容量差值在星座点数较多时同样处在qam和gam之间。
[0076]
图4所示为提出星座图可达到的最大传输速率随着信噪比snr变化的曲线，其中q＝20。可以看出，提出星座图(无papr约束)可达到的最大传输速率相比于其他星座图在不同信噪比条件下更接近于信道容量，提出星座图(低papr)可达到的最大传输速率在整个信噪比取值范围上略低于gam和apsk，且在信噪比较高时比qam低，但当信噪比较低(约小于20db)时，提出星座图(低papr)可达到的最大传输速率高于qam。
[0077]
图5为提出星座图的papr随q变化的曲线，其中snr＝8db。从图5可以看出，提出星座图的papr在不同星座点数的情况下均明显低于gam，提出星座图(低papr)具有比提出星座图(无papr约束)更低的papr。当q≤6时，qam的papr较之于提出的星座图更低，而当q≥7时，相比于qam，提出的星座图(低papr)具有更低的papr，且当星座点数继续增加，提出的星座图(低papr)在papr上的优势更加明显。综合图2-5，可以看到，提出的星座图(低papr)牺牲了较少的容量差值性能，换取了papr的大幅度降低，尤其在星座点数较大时这种性能转化愈加明显。