一种基于FPGA的poseidon哈希算法的优化方法与流程

一种基于fpga的poseidon哈希算法的优化方法
技术领域
1.本发明涉及一种哈希算法的优化，具体涉及一种基于fpga的poseidon哈希算法的优化方法。


背景技术：

2.用于密码学的hash函数有严格的要求，单向性：从数据求散列值很容易，但不能倒推，或者倒推十分困难，理论上不可行。无相关性：要求在输入有一点点改变的情况下，要产生完全不同的输出，这样，从散列值完全不能看出数据之间的相关性。唯一性：不能通过不同的数据产生相同的hash值，这里说的不能是基本上不能人为实现，也就是说概率极小，此特性也可以成为碰撞安全性。在分布式存储领域中，要把大容量gb级的数据打散加密，这时要用到poseidonhash算法。
3.poseidon哈希可将若干个gf(p)中的元素映射为单个gf(p)中的元素，形如其中t为输入个数，p为有限域的阶数。由于零知识证明如zksnark、zkstark、bulletproof等使用了大量pedersen哈希、sha256等哈希算法以保证完整性，然而在证明及验证时效率较低，而poseidon哈希则基于传统哈希设计方法(类spn结构)，是有限域上较为高效的哈希算法，且支持零知识证明中使用的多数曲线(bn、bls、ed25519)。
4.poseidon哈希可用于以下场景：零知识证明中的承诺函数，在该类协议中，秘密值通常通过承诺函数加密并生成零知识证明；将多个有限域中元素映射为一个元素或变长哈希；用于merkle树中叶子节点的存在性证明，如证明某个节点属于某一个树。


技术实现要素：

5.本发明所要解决的技术问题是目前在pfga上进行poseidon哈希算法的运算工作量巨大，现有的硬件水平无法跟上大规模的数据量运算，需要优化运算方式，使得现有的pfga能过处理，本技术文件目的在于提供一种基于fpga的poseidon哈希算法的优化方法，上述问题。
6.本发明通过下述技术方案实现：
7.一种基于fpga的poseidon哈希算法的优化方法，所述方法包括如下步骤：在fpga内对poseidon算法参数及流程优化和底层蒙哥马利模乘优化两方面进行优化；其中在poseidon哈希算法参数及流程优化中通过常量计算、矩阵计算、常量及矩阵选择和算法流程优化；在底层蒙哥马利模乘优化中将蒙哥马利算法输入值由标准值转化为蒙哥马利形式，并通过将模乘、幂模运算中计算开销大的除法运算转化为计算开销小的移位和乘法，提高计算效率。
8.目前poseidon哈希主要由若干轮轮函数组成，轮函数主要包括三个部分：
9.1.addroundconstants，记为arc()，即与常量相加；
10.2.subwords，记为s-box()或sb()，包含一个非线性变换；
11.3.mixlayer，记为m()，混淆函数，一般为一个常量mds矩阵的乘积。
12.轮函数有两种：full s-box和partial s-box，full s-box轮函数中每一轮各输入均需计算s-box值，即需要计算arc()
→
sb()
→
m()完整过程，而partial s-box每一轮只需计算一个输入值的s-box。
13.poseidon哈希算法流程为：
14.先进行rf轮full s-box，再进行r
p
轮partial s-box，最后再进行rf轮full s-box，共需计算(2trf+tr
p
)次arc()、m()运算，(2trf+r
p
)次sb()运算，其中t为输入元素个数加1。
15.进一步地，所述步骤中的常量计算采用的spn结构中，由于交换线性变换阶段和常量计算都是线性的，通过交换计算顺序，进行等价转换。对于每一轮的常量ci，转化后表示为其中mc为第i轮线性变换(mixlayer)。
16.在partial s-box阶段，可以利用该性质将常量计算部分从最后一轮循环置换到开始部分。因此，需要将常量分为两部分，一部分用于partial s-box中带有s-box的计算，一部分用于partial s-box无需s-box的计算。通过该种形式，除了最初rf轮结束后需要再加一个常量，其余常量可以加在s-box输出后。
17.进一步地，所述步骤中的矩阵计算中的交换线性变换阶段，计算与mds矩阵的乘积时，使用多线程及并行计算，提高矩阵运算效率。需要计算与mds矩阵的乘积，t
×
tmds矩阵记为
[0018][0019]
其中为(t-1)
×
(t-1)的mds矩阵，v是1
×
(t-1)矩阵，ω为(t-1)
×
1的向量。通过转化，可将矩阵m表示为：
[0020][0021]
其中i为(t-1)
×
(t-1)的单位矩阵。
[0022]
根据常量计算中结论，可将partial s-box和mixlayer(与m
′
乘积部分)顺序调换，调换后，在partial s-box阶段，每一次线性变换(mixlayer)变为与矩阵m
″
的乘积。由于m
″
中(t-1)
2-(t-1)＝t
2-3t+2个元素为0，因此为稀疏矩阵，可减少线性变换(mixlayer)阶段的乘法次数。
[0023]
此外，由于矩阵乘法目前软件实现采用两层循环嵌套方式，复杂度为o(n2)，因此可使用多线程或并行计算的方式，提高矩阵运算效率。
[0024]
进一步地，所述步骤中的算法流程优化时，将poseidon哈希算法的输入定为11个256bit大整数，输出定为1个256bit大整数，进行实现和优化，算法流程如下：
[0025]
s1：将11个输入值扩充为12个256bit大整数；
[0026]
s2：在12个输入值加前12个常量；
[0027]
s3：进行4轮full s-box，每轮full s-box包含12个指数运算，12个加法运算，以及
矩阵乘积，返回12个大整数；
[0028]
s4：进行57轮partial s-box，每轮partial s-box包含1个指数运算，1个加法运算，以及稀疏矩阵乘法，返回12个大整数；
[0029]
s5：进行3轮full s-box，每轮full s-box包含12个指数运算，12个加法运算，以及矩阵乘积，返回12个大整数；
[0030]
s6：进行最后一轮full s-box，包含12个指数运算，以及矩阵乘积，返回12个大整数；
[0031]
s7：输出第二个元素，为256bit大整数。
[0032]
进一步地，所述步骤中的蒙哥马利算法包括模乘、约减和幂模运算，其采用的蒙哥马利算法输入值转化为蒙哥马利形式后表示为x＝xrmodn，其中x为标准值，x为蒙哥马利表示法，r为蒙哥马利参数，mod为求余函数。
[0033]
蒙哥马利算法是目前计算大数模乘、幂模较为高效的算法之一，主要思想是将模乘、幂模运算中计算开销较大的除法运算转化为计算开销较小的移位和乘法，从而提高计算效率。
[0034]
蒙哥马利算法主要包括模乘、约减和幂模运算，蒙哥马利算法输入值需由标准值转化为蒙哥马利形式，即x＝xrmodn，其中x为标准值，x为蒙哥马利表示法，r为蒙哥马利参数。
[0035]
蒙哥马利模乘：计算xyr-1
modn
[0036]
蒙哥马利约减：计算xr-1
modn
[0037]
蒙哥马利幂模：计算xymodn
[0038]
在计算大整数乘法(如256bit大整数)时，通常会根据操作系统和cpu的位数将大整数表示为若干个计算机中的字，如64位系统中一个字为64bit，因此可将256bit表示为4个64bit(字)，便于存储和计算。
[0039]
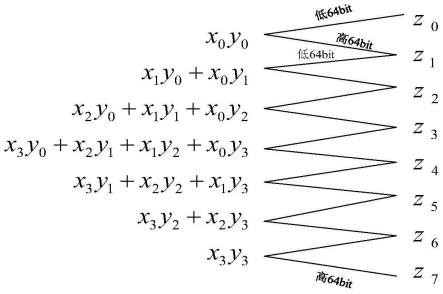
对于蒙哥马利算法，也可将256bit大整数表示为4个64bit大整数的乘法，进行计算。蒙哥马利模乘需先计算一次大整数乘法，再计算一次蒙哥马利约减。若将256bit大整数表示为4个64bit整数，在计算乘法z＝xy，其中x＝x0+x1a+x2a2+x3a3,y＝y0+y1a+y2a2+y3a3，a＝2
64
时，一般可按如下方式计算
[0040][0041]
其中z0,...,z7为64bit整数，相关关系如下图18所示，上述过程具体体现在蒙哥马利模乘第1步中，在计算平方时，
[0042]
z＝x
02
+2x0x1a+(x
12
+2x0x2)a2+2(x1x2+x0x3)a3+(x
22
+2x1x3)a4+2x2x3a5+x
32
a6[0043]
可减少乘法的计算次数，相比普通乘法效率稍高一点，因此通常将平方计算和普
通乘法单独实现。
[0044]
本发明与现有技术相比，具有如下的优点和有益效果：
[0045]
1、本发明一种基于fpga的poseidon哈希算法的优化方法，基于fpga实现了poseidon哈希算法，并对参数、算法流程等进行了优化，提高了算法效率，在硬件设备的支持下，可应用于零知识证明、区块链、分布式存储计算等场景；
[0046]
2、本发明一种基于fpga的poseidon哈希算法的优化方法，基于fpga实现了底层蒙哥马利算法，并进行了优化，提高了大整数运算效率；
附图说明
[0047]
此处所说明的附图用来提供对本发明实施例的进一步理解，构成本技术的一部分，并不构成对本发明实施例的限定。在附图中：
[0048]
图1为本发明蒙哥马利约减硬件实现逻辑图。
[0049]
图2为在约减硬件下的取模运算图。
[0050]
图3为在约减硬件下的单个乘法器输出图。
[0051]
图4为在约减硬件下的总乘法器输出图。
[0052]
图5为在约减硬件下的加法器输出图。
[0053]
图6为在约减硬件下的除法器输出图。
[0054]
图7为在约减硬件下的减法器输出图。
[0055]
图8为本发明蒙哥马利模平方硬件实现逻辑图。
[0056]
图9为在平方硬件下的运算图。
[0057]
图10为在平方硬件下的截断图。
[0058]
图11为在平方硬件下的加法器图。
[0059]
图12为在平方硬件下的减法器图。
[0060]
图13为本发明蒙哥马利模乘运算硬件实现逻辑图。
[0061]
图14为在模乘运算硬件下的加乘器图。
[0062]
图15为在模乘运算硬件下的取模图。
[0063]
图16为在模乘运算硬件下的加法器图。
[0064]
图17为在模乘运算硬件下的减法器图。
[0065]
图18大整数乘法示意图。
具体实施方式
[0066]
为使本发明的目的、技术方案和优点更加清楚明白，下面结合实施例和附图，对本发明作进一步的详细说明，本发明的示意性实施方式及其说明仅用于解释本发明，并不作为对本发明的限定。
[0067]
实施例
[0068]
本发明一种基于fpga的poseidon哈希算法的优化方法，在进行优化时，由于使用xilinx dsp ip的输入位宽是27x18bits，因此进一步将最小单元乘法操作拆解成16bits宽度，即将256bit大整数表示为16个16bit的整数，便于电路实现。蒙哥马利算法实现及优化如图1～7所示：蒙哥马利约减：计算xr-1
modn，其中x＝xrmodn，其中x为标准值，x为蒙哥马利
表示法，r为蒙哥马利参数(一般可取2
256
)，需要提前计算参数ω＝-n-1
mod2
64
。
[0069]
4乘64bit蒙哥马利约减流程如下：
[0070][0071][0072]
如图8～12所示，蒙哥马利模平方：计算x2r-1
modn，其中x＝xrmodn，其中x为标准值，x为蒙哥马利表示法，r为蒙哥马利参数(一般可取2
256
)，需要提前计算参数ω＝-n-1
mod2
64
。计算时，先计算t＝x2，再计算一次蒙哥马利约减即可，4乘64bit蒙哥马利模平方流程如下：
[0073][0074]
如图13～17所示，蒙哥马利模乘也可看作一次大整数乘法和一次蒙哥马利约减计算，计算xyr-1
modn，其中x＝xrmodn，y＝yrmodn，其中x,y为标准值，x,y为蒙哥马利表示法，r为蒙哥马利参数(一般可取2
256
)，需要提前计算参数ω＝-n-1
mod2
64
。
[0075]
通过cios方法可对上述蒙哥马利乘法进行优化，主要思路是在进行乘法的同时进行蒙哥马利约减，即进行一轮大整数乘法(4组64bit乘法)，再进行一轮蒙哥马利约减，主要流程如下：
[0076][0077]
以上所述的具体实施方式，对本发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本发明的具体实施方式而已，并不用于限定本发明的保护范围，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。