一种基于SM2的改良的定向签名算法的制作方法

一种基于sm2的改良的定向签名算法
技术领域
1.本发明涉及一种定向签名算法，具体是指一种基于sm2的改良的定向签名算法。


背景技术：

2.定向签名算法可以用于验证数据的完整性和保密性，基于sm2的改良的定向签名算法是加密签名算法的一种。
3.现有的定向签名算法大部分采用椭圆曲线离散对数问题都存在难处理性和低安全性，但加密签名具有可验证性的属性，任何人都可以利用签名对数据进行验证。针对部分签名者或验证者的不想公开的隐私数据，他们并不希望所有人都能验证数据的真实性。
4.所以，一种基于sm2的改良的定向签名算法成为人们亟待解决的问题。


技术实现要素：

5.本发明要解决的技术问题是现有的定向签名算法大部分采用椭圆曲线离散对数问题都存在难处理性和低安全性。
6.为解决上述技术问题，本发明提供的技术方案为：一种基于sm2的改良的定向签名算法，包括签名者和验证者，设定用户a作为签名者，用户b作为验证者，所述签名者具有长度为entlen比特的可辨别表示ida、私钥da、公钥pa＝(xa,ya)、代签名的消息为m；
7.所述验证者具有长度为entlen比特的私钥db公钥pb＝(xb,yb)；
8.预计算出za＝h256(entlen∥ida∥a∥b∥gx∥gy∥xa∥ya)；
9.作为签名者的用户a进行传输待签名的消息m，执行以下步骤：
10.步骤1、计算m*＝za∥m；
11.步骤2、计算e＝hv(m*)，将e的数据类型转换为整数；
12.步骤3、用随机数发生器产生随机数k∈[1,n-1]；
[0013]
步骤4、计算椭圆曲线点(x1,y1)＝k*g，将x1的数据类型转换为整数；
[0014]
步骤5、计算椭圆曲线点(x2,y2)＝k*pb，将x2的数据类型转换为整数；
[0015]
步骤6、计算r＝(e+x1+x2)mod n，若r＝0或r+k＝n，则返回步骤3；
[0016]
步骤7、计算s＝((1+da)-1
*(k-r*da))mod n，若s＝0，则返回步骤3；
[0017]
步骤8、将r、s的数据类型转换为字节串，得到消息m的签名为(r、s)；
[0018]
作为验证者的用户b为了检验收到的消息m及其数字签名(r、s)，执行以下步骤：
[0019]
步骤1、检验r∈[1,n-1]是否成立，若不成立则验证不通过；
[0020]
步骤2、检验s∈[1,n-1]是否成立，若不成立则验证不通过；
[0021]
步骤3、计算m*＝za∥m；
[0022]
步骤4、计算e＝hv(m*)，将e的数据类型转换为整数；
[0023]
步骤5、计算t＝(r+s)mod n，若t＝0，则验证不通过；
[0024]
步骤6、计算椭圆曲线点pk＝(x1,y1)＝s*g+t*pa，将x1的数据类型转换为整数；
[0025]
步骤7、计算椭圆曲线点(x2,y2)＝db*pk，将x2的数据类型转换为整数；
[0026]
步骤8、将x1的数据类型转换为整数，计算r1＝(e+x1+x2)mod n，检验r1＝r是否成立，若成立则验证通过；若不成立验证不通过。
[0027]
进一步的，所述h256采用sm3杂凑算法，但不限于sm3杂凑算法。
[0028]
进一步的，随机数生成技术包括但不限于salsa20、ansi x9.17、aes-ctr-drbg、isaac。
[0029]
进一步的，所述e的数据类型转换为整数，是按照gm/t00o3.1—20124,2.4和4,2,3给出的方法进行数据类型的转换；
[0030]
所述x1的数据类型转换为整数，是按照gm/t0003.1—20.12的4.2.8给出的方法进行数据类型的转换；
[0031]
所述x2的数据类型转换为整数，也是按照gm/t0003.1—20.12的4.2.8给出的方法进行数据类型的转换。
[0032]
进一步的，所述的xa、ya：是指用户a的密钥对，包括其私钥da和公钥pa＝[da]g＝(xa,ya)；
[0033]
所述xb、yb：是指用户b的密钥对，包括其私钥db和公钥pb＝[db]g＝(xb,yb)；
[0034]
所述za是关于用户a的可辨别标识、部分椭圆曲线系统参数和用户a公钥的杂凑值；
[0035]
所述a、b：是指有限域fq中的元素，它们定义fq上的一条椭圆曲线e；
[0036]
所述gx、gy是fq中的两个元素；
[0037]
所述m*是指待验证消息；
[0038]
所述e是密码杂凑函数作用于消息m*的输出值；
[0039]
所述g是椭圆曲线的一个基点，其阶为素数；
[0040]
所述(r、s)是指发送的签名。
[0041]
本发明与现有技术相比的优点在于：本发明包含多种密码的应用，针对签名者或验证者不想公开的隐私数据，通过密码设置以及相关算法的应用，实现了只有签名者和验证者能验证数据的真实性，不是所有人都可以验证数据的真实性；本发明确保了数据的完整性、保密性；本发明设计合理，值得大力推广。
附图说明
[0042]
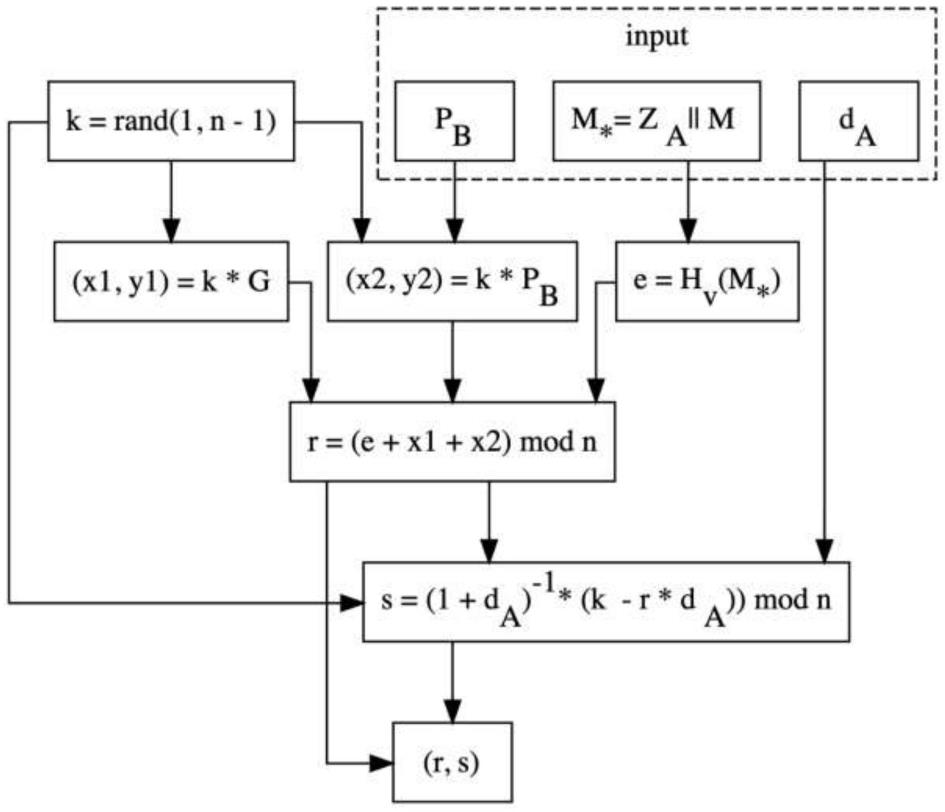
图1是本发明一种基于sm2的改良的定向签名算法中作为签名者的用户a进行传输待签名的消息m的执行流程。
[0043]
图2是本发明一种基于sm2的改良的定向签名算法中作为验证者的用户b为了检验收到的消息m及其数字签名(r、s)的执行流程。
具体实施方式
[0044]
下面结合附图对本发明一种基于sm2的改良的定向签名算法做进一步的详细说明。
[0045]
结合附图1-2，对本发明进行详细介绍。
[0046]
一种基于sm2的改良的定向签名算法，包括签名者和验证者，设定用户a作为签名者，用户b作为验证者，所述签名者具有长度为entlen比特的可辨别表示ida、私钥da、公钥
pa＝(xa,ya)、代签名的消息为m；
[0047]
所述验证者具有长度为entlen比特的私钥db公钥pb＝(xb,yb)；
[0048]
预计算出za＝h256(entlen∥ida∥a∥b∥gx∥gy∥xa∥ya)；
[0049]
作为签名者的用户a进行传输待签名的消息m，执行以下步骤：
[0050]
步骤1、计算m*＝za∥m；
[0051]
步骤2、计算e＝hv(m*)，将e的数据类型转换为整数；
[0052]
步骤3、用随机数发生器产生随机数k∈[1,n-1]；
[0053]
步骤4、计算椭圆曲线点(x1,y1)＝k*g，将x1的数据类型转换为整数；
[0054]
步骤5、计算椭圆曲线点(x2,y2)＝k*pb，将x2的数据类型转换为整数；
[0055]
步骤6、计算r＝(e+x1+x2)mod n，若r＝0或r+k＝n，则返回步骤3；
[0056]
步骤7、计算s＝((1+da)-1
*(k-r*da))mod n，若s＝0，则返回步骤3；
[0057]
步骤8、将r、s的数据类型转换为字节串，得到消息m的签名为(r、s)；
[0058]
作为验证者的用户b为了检验收到的消息m及其数字签名(r、s)，执行以下步骤：
[0059]
步骤1、检验r∈[1,n-1]是否成立，若不成立则验证不通过；
[0060]
步骤2、检验s∈[1,n-1]是否成立，若不成立则验证不通过；
[0061]
步骤3、计算m*＝za∥m；
[0062]
步骤4、计算e＝hv(m*)，将e的数据类型转换为整数；
[0063]
步骤5、计算t＝(r+s)mod n，若t＝0，则验证不通过；
[0064]
步骤6、计算椭圆曲线点pk＝(x1,y1)＝s*g+t*pa，将x1的数据类型转换为整数；
[0065]
步骤7、计算椭圆曲线点(x2,y2)＝db*pk，将x2的数据类型转换为整数；
[0066]
步骤8、将x1的数据类型转换为整数，计算r1＝(e+x1+x2)mod n，检验r1＝r是否成立，若成立则验证通过；若不成立验证不通过。
[0067]
所述h256采用sm3杂凑算法，但不限于sm3杂凑算法。
[0068]
随机数生成技术包括但不限于salsa20、ansi x9.17、aes-ctr-drbg、isaac。
[0069]
所述e的数据类型转换为整数，是按照gm/t00o3.1—20124,2.4和4,2,3给出的方法进行数据类型的转换；
[0070]
所述x1的数据类型转换为整数，是按照gm/t0003.1—20.12的4.2.8给出的方法进行数据类型的转换；
[0071]
所述x2的数据类型转换为整数，也是按照gm/t0003.1—20.12的4.2.8给出的方法进行数据类型的转换。
[0072]
所述的xa、ya：是指用户a的密钥对，包括其私钥da和公钥pa＝[da]g＝(xa,ya)；
[0073]
所述xb、yb：是指用户b的密钥对，包括其私钥db和公钥pb＝[db]g＝(xb,yb)；
[0074]
所述za是关于用户a的可辨别标识、部分椭圆曲线系统参数和用户a公钥的杂凑值；
[0075]
所述a、b：是指有限域fq中的元素，它们定义fq上的一条椭圆曲线e；
[0076]
所述gx、gy是fq中的两个元素；
[0077]
所述m*是指待验证消息；
[0078]
所述e是密码杂凑函数作用于消息m*的输出值；
[0079]
所述g是椭圆曲线的一个基点，其阶为素数；
[0080]
所述(r、s)是指发送的签名。
[0081]
本发明一种基于sm2的改良的定向签名算法的具体实施过程如下：
[0082]
作为签名者的用户a进行传输待签名的消息m，执行以下步骤：
[0083]
步骤1、计算m*＝za∥m；
[0084]
步骤2、计算e＝hv(m*)，将e的数据类型转换为整数；
[0085]
步骤3、用随机数发生器产生随机数k∈[1,n-1]；
[0086]
步骤4、计算椭圆曲线点(x1,y1)＝k*g，将x1的数据类型转换为整数；
[0087]
步骤5、计算椭圆曲线点(x2,y2)＝k*pb，将x2的数据类型转换为整数；
[0088]
步骤6、计算r＝(e+x1+x2)mod n，若r＝0或r+k＝n，则返回步骤3；
[0089]
步骤7、计算s＝((1+da)-1
*(k-r*da))mod n，若s＝0，则返回步骤3；
[0090]
步骤8、将r、s的数据类型转换为字节串，得到消息m的签名为(r、s)；
[0091]
作为验证者的用户b为了检验收到的消息m及其数字签名(r、s)，执行以下步骤：
[0092]
步骤1、检验r∈[1,n-1]是否成立，若不成立则验证不通过；
[0093]
步骤2、检验s∈[1,n-1]是否成立，若不成立则验证不通过；
[0094]
步骤3、计算m*＝za∥m；
[0095]
步骤4、计算e＝hv(m*)，将e的数据类型转换为整数；
[0096]
步骤5、计算t＝(r+s)mod n，若t＝0，则验证不通过；
[0097]
步骤6、计算椭圆曲线点pk＝(x1,y1)＝s*g+t*pa，将x1的数据类型转换为整数；
[0098]
步骤7、计算椭圆曲线点(x2,y2)＝db*pk，将x2的数据类型转换为整数；
[0099]
步骤8、将x1的数据类型转换为整数，计算r1＝(e+x1+x2)mod n，检验r1＝r是否成立，若成立则验证通过；若不成立验证不通过。
[0100]
本发明包含多种密码的应用，针对签名者或验证者不想公开的隐私数据，通过密码设置以及相关算法的应用，实现了只有签名者和验证者能验证数据的真实性，不是所有人都可以验证数据的真实性；本发明确保了数据的完整性、保密性；本发明设计合理，值得大力推广。
[0101]
以上对本发明及其实施方式进行了描述，这种描述没有限制性，附图中所示的也只是本发明的实施方式之一，实际的结构并不局限于此。总而言之如果本领域的普通技术人员受其启示，在不脱离本发明创造宗旨的情况下，不经创造性的设计出与该技术方案相似的结构方式及实施例，均应属于本发明的保护范围。