一种节点接入和飞行策略联合优化的无人机信息收集方法

1.本发明属于无人机辅助通信技术领域，具体涉及一种节点接入和飞行策略联合优化的无人机信息收集方法。


背景技术：

2.近年来5g通信技术的飞速发展推动了物联网(internet of things,iot)在环境监测、物流管理、农业等众多领域的应用，iot设备得以数亿计的铺设。
3.但是，庞杂化、需求多样化的信息导致静态信息收集系统显露出一些不足，制约了其进一步发展。一方面，在通信覆盖范围受限区域或小区边缘部署的iot设备面临着上传效率低下，甚至无法上传信息至公网的问题；另一方面，大多数iot设备所搭载的射频通信模块的传输距离有限，频繁采用多跳传输形式汇聚信息上传至公网的信息采集模式导致传感器在上传信息至公网时，除自身传输能耗外，还可能增加额外传感器的路由能耗。
4.因此，为了克服静态信息收集的局限性，利用无人机辅助通信成为一种研究方向，即利用无人机的视距传输和强机动性对物联网节点实现高效的信息收集。
5.然而，针对自然保护区、田野、风力发电厂等iot设备分布稀疏场景的无人机信息收集系统的研究甚少，且应用悬停或匀速直线飞行策略的无人机信息收集系统在该场景存在一定的局限性。因为稀疏分布的iot设备的数据量的累计通常在100m以下，由于中小型旋翼无人机的悬停能耗小于速度较低情况下的匀速飞行能耗，悬停策略的数据收集过程会造成无人机能量的浪费和任务总时间的增加，而匀速直线飞行策略因通信带宽的限制会导致数据收集的不完整性。
6.所以，无人机在节点稀疏分布的物联网场景中对节点进行信息收集任务时，其推进能耗的消耗要远远大于通信能耗，并且由于节点通信半径和数据收集完整性的限制，悬停、匀速飞行等无人机飞行策略具有明显的局限性。因此，针对节点稀疏分布的物联网场景进行节点信息收集任务时，如何对无人机能耗和节点接入进行优化等问题正成为亟需解决的问题。


技术实现要素：

7.本发明旨在提供一种节点接入和飞行策略的无人机信息收集方法，用于解决节点稀疏分布物联网场景下无人机能耗和数据收集完整性联合优化问题。
8.本发明的技术方案是：
9.一种节点接入和飞行策略联合优化的无人机信息收集方法，包括以下步骤：
10.步骤s1，定义包含无人机能耗成本和运行时间成本的加权代价函数；
11.即
12.cost
ε
＝εcoste+(1-ε)cost
t
ꢀꢀꢀꢀꢀꢀ
(20)
13.具体的：
14.定义权衡无人机能耗成本和运行时间成本的加权因子ε，其中0≤ε≤1；
15.定义无人机能耗成本其中，σe可解释为单位能量的代价，单位可表示为价格/焦耳，为无人机进行一次任务的能量消耗；
16.定义无人机单次任务的运行时间成本cost
t
＝σ
t
t；其中，σ
t
可解释为单位时间的代价，单位可表示为价格/秒，t为无人机单次任务的运行时间；
17.无人机单次任务的运行时间t可由多段匀速时间和加减速时间表示为：
[0018][0019]
步骤s2，设置优化问题(p1)：在无人机传输、缓存、功率和节点通信半径的限制下，通过联合优化节点采集顺序o、无人机额定速度v1、v2和节点接入选择方案αk[n]以最小化代价函数；即该优化问题表述如(p1)：
[0020][0021]
s.t.
[0022]
v[n]＝v[n-1]+a[n-1]δ
t
，n＝2，
…
，n
ꢀꢀꢀꢀꢀꢀ
(22a)
[0023][0024]amin
≤||a[n]||≤a
max
，v
min
≤||v[n]||≤v
max
，n＝1，
…
，n
ꢀꢀꢀꢀꢀꢀ
(22c)
[0025]
q[n]-q[n-1]＝v[n-1]δ
t
+0.5a[n-1]δ
t2
，n＝2，
…
，n
ꢀꢀꢀꢀꢀ
(22d)
[0026]
q[1]＝qi＝q0，q[n]＝qf＝q0ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(22e)
[0027][0028][0029][0030][0031][0032]
[0033][0034][0035][0036]
具体的：
[0037]
代价函数cost
ε
是一个关于无人机能耗成本coste和任务总时间成本cost
t
的加权函数，如步骤s1所示；
[0038]
定义无人机运动约束组，包括无人机速度约束(22a)、无人机加减速约束(22b)、无人机最大速度和最大加速度约束(22c)、无人机路程约束(22d)和无人机始末点约束(22e)，确保无人机能够在节点问和节点的通信范围内匀速飞行；
[0039]
定义节点接入选择约束组，包括节点数据量约束(22f)、节点数据采集时间和无人机匀飞时间约束(22g)和单一时隙内节点接入约束(22h)-(22i)，确保了无人机能够收集到各节点的完整数据；
[0040]
定义无人机缓存约束(22j)和无人机能耗约束(22k)，以保证无人机采集数据量超出缓存以及能耗过低；
[0041]
定义无人机多段匀速约束组，包括无人机在节点内的匀速时间约束(221)、无人机在节点间的匀速时间约束(22m)和无人机首次抵达各节点通信半径的时隙约束，确保无人机能准确无人机的加减速和匀速；
[0042]
步骤s3，采用凸松弛方法将优化问题(p1)转化问题(p2)，确保目标函数的凸性：
[0043]
具体的：
[0044]
引入变量cost，将代价函数cost
ε
转化成：
[0045]
cost
ε
≤cost
ꢀꢀꢀꢀꢀꢀ
(23)
[0046]
引入松弛变量ζm、ξ
m，m+1
处理目标函数中能耗模型的非凸项，表达式如下所示：
[0047][0048][0049]
将非放射约束(221)-(22m)、(24)和(25)转换为不等式约束，则问题p1转化成问题p2：
[0050][0051]
s.t.
[0052]
cost
ε
≤cost
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(30a)
[0053][0054][0055][0056][0057]
(22a)-(22k)，(22n)
[0058]
步骤s4，采用分布线性法和完全平方公式将问题(p2)转化为问题(p3)：
[0059]
具体的：
[0060]
采用分步线性法处理分段函数(22b)，将其转化如下所示的线性不等式
[0061][0062][0063][0064][0065]ai，m
∈{0，1}，1≤i≤4，0≤m≤m+1
ꢀꢀꢀꢀꢀꢀꢀꢀ
(31e)
[0066]
处理线性不等式中“二进制变量
×
连续变量”的函数项a
1，m
(v
m，m+1-vm)，采用大m法对其转化；首先引入变量z
1，1，m
，令z
1，1，m
＝a
1，m
(v
m，m+1-vm)；假设v
m，m+1-vm的有限上界为m，可以看出，若a
1，m
＝0则z
1，1，m
＝0，当a
1，m
＝1时，z
1，1，m
≤m；因此，可以得到z
1，1，m
≤a
1，m
m；此外，由于z
1，1，m
一直小于v
m，m+1-vm，并且当a
1，m
＝1时z
1，1，m
＝v
m，m+1-vm；因此，函数项a
1，m
(v
m，m+1-vm)可以转化为：
[0067]
0≤z
1，1，m
≤v
m，m+1-vmꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(33)
[0068]z1，1，m
≥v
m，m+1-v
m-(1-a
1，m
)m
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(34)
[0069]
式(31b)-(31d)内其他的“二进制变量
×
连续变量”表示形式的函数项亦采用上述方法进行线性化；
[0070]
引入辅助变量ηm、η
m，m+1
来处理约束(30b)和约束(30c)内的非凸项，使其满足：
[0071][0072]
[0073]
针对式(35)-(36)中非递减凸函数相乘的形式，采用完全平方公式将其转化为：
[0074][0075][0076]
针对中的非递减凸函数相乘形式的非凸项，引入辅助变量εm、ε
m，m+1
，使其满足：
[0077][0078][0079]
采用完全平方公式处理式(39)-(40)，处理结果如下所示：
[0080][0081][0082]
将松弛变量ηm、η
m，m+1
、εm和ε
m，m+1
分别引入约束(30b)-(30c)和(22k)，则问题(p2)可以转化为问题(p3)：
[0083][0084]
s.t.
[0085][0086][0087][0088]
(22a)，(22c)-(22k)，(22n)，(30a)，(30d)-(30e)，
[0089]
(31a)-(31e)，(37)-(38)，(41)-(42)
[0090]
步骤s5，采用连续凸逼近方法将问题(p3)转化为带规则凸约束的混合整数问题(p4)：
[0091]
具体的：
[0092]
针对约束(22f)中的非凸项rk[n]，采用第r次迭代的局部最优值qr[n]，通过一阶泰勒展开得到其下界
[0093][0094]
其中，
[0095]
[0096][0097]
处理约束(22f)中的乘积项αk[n]rk[n]，引入辅助变量γk[n]，使其满足γk[n]＝αk[n]rk[ftk+τi]；
[0098]
采用大m法将其转化为如下约束：
[0099]
0≤γk[n]≤rk[ftk+τi]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(47)
[0100]
γk[n]≥rk[ftk+τi]-(1-αk[n])m
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(48)
[0101]
针对约束(30d)和(30e)中的平方项，分别对平方项ζ
m2
、v
m2
、ζ
m，m+12
和v
m，m+12
在在和处进行一阶泰勒展开，如下所示：
[0102][0103][0104]
针对约束(37)中存在两个凸函数之差(dc)的结构，采用逐次凸逼近方法将其转化为凸结构；首先在第r次迭代时，将在点处进行一阶泰勒展开：
[0105][0106]
接着，引入辅助变量μ
1，m
，使得并将中按照式(51)中的方式进行展开，可以得到：
[0107][0108]
式(52)可进一步简化为：
[0109][0110]
针对与式(37)结构相似的式(38)和式(41)-(42)，可以得到：
[0111][0112]
[0113][0114]
此时，问题(p3)可以根据任意局部点qr[n]、[n]、p(vm)r、和p(v
m，m+1
)r及其下界表达式近似为带有迭代值和规则凸约束的混合整数问题(p4)：
[0115][0116]
s.t.
[0117]
(22a)，(22c)-(22e)，(22g)-(22k)，(22n)，(30a)，
[0118]
(31a)-(31e)，(43a)-(43c)，(44)，(47)-(50)，(53)-(56)
[0119]
步骤s6，采用sca技术通过连续迭代的方式优化问题(p4)，进而使得问题(p1)满足kkt条件，并得到解决；问题(p4)具体算法包括：
[0120]
s6.1：初始化(p4)解空间a0，误差精度∈＞0，迭代次数r＝0；
[0121]
s6.2：求解(30)，(33)-(34)和(37)-(40)在第r迭代中一阶泰勒展开的值；
[0122]
s6.3：将ar带入(p4)并得到最优解a
*
；
[0123]
s6.4：更新解空间a
r+1
＝a
*
；
[0124]
s6.5：r＝r+1；
[0125]
s6.6：|a
r-a
r-1
|＜∈。
[0126]
本发明的有益效果在于：
[0127]
(1)针对设备稀疏分布和上传数据较少的情况，考虑节点通信半径限制，本发明采用多段匀速飞行策略，联合优化无人机速度和节点接入选择方案，以最小化代价函数为目标，并建立相关问题模型。
[0128]
(2)由于原问题模型是个混合整数非凸优化问题，很难直接求解。本发明对问题中的约束和代价函数进行了凸松弛，将其转化为带规则凸约束的混合整数问题，并逐次凸逼近(sca)技术，提出了一种迭代算法求得问题的局部最优解，该算法满足karush-kuhn-tucker(kkt)条件的解并收敛。
[0129]
(3)通过数值仿真验证了所提算法的有效性，验证了节点接入方案和多段匀速飞行策略的匹配程度，探究了所提算法在能耗、任务时间和代价因子间的关系，并在保证节点信息收集完整性的前提下，提高了无人机信息收集的效率。
附图说明
[0130]
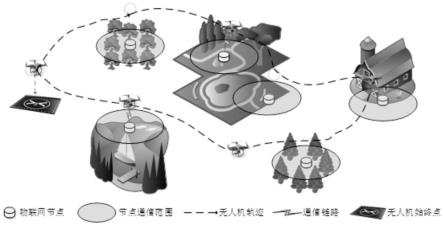
图1为本发明实施例提供的一种节点接入和飞行策略联合优化的无人机信息收集方法的系统模型图；
[0131]
图2为本发明实施例提供的一种节点接入和飞行策略联合优化的无人机信息收集方法中的nafs算法的三种不同加权因子的代价函数的收敛性对比图；
[0132]
图3为本发明实施例提供的一种节点接入和飞行策略联合优化的无人机信息收集方法中的nafs算法ε＝0.5时无人机的飞行轨迹图；
[0133]
图4为本发明实施例提供的一种节点接入和飞行策略联合优化的无人机信息收集
方法中的nafs算法ε＝0.5时无人机的飞行速度和iot设备的接入选择方案；
[0134]
图5为本发明实施例提供的一种节点接入和飞行策略联合优化的无人机信息收集方法中的无人机能耗和速率随代价加权因子ε的变化曲线图；
[0135]
图6为本发明实施例提供的一种节点接入和飞行策略联合优化的无人机信息收集方法中的无人机能耗和总任务时间随代价加权因子ε的变化图；
[0136]
图7为本发明实施例提供的一种节点接入和飞行策略联合优化的无人机信息收集方法中的不同飞行策略下无人机的能耗随iot设备数据量的变化曲线图；
[0137]
图8为本发明实施例提供的一种节点接入和飞行策略联合优化的无人机信息收集方法中的不同代价因子下的无人机能耗随iot设备数据量的变化曲线图；
[0138]
图9为本发明实施例提供的一种节点接入和飞行策略联合优化的无人机信息收集方法中的无人机总任务时间随iot设备数据量的变化曲线图。
具体实施方式
[0139]
下面结合附图和具体实施例对本发明作进一步说明，以使本领域的技术人员可以更好的理解本发明并能予以实施，本发明的实施方式不限于此。
[0140]
1、系统模型
[0141]
如图1所示，本发明考虑一个节点分布稀疏的物联网场景，使用一个旋翼无人机与随机分布的k个点通信、收集并上传数据。其中，节点的集合表示为节点sk的水平位置表示为由于节点感知信息存在视频、照片等不同类型数据导致的上传数据量的差异性，采用表示节点sk所需上传据量大小。为了便于分析，本发明忽略节点因设计不同导致通信范围不一的问题，假设所有节点的有效通信范围均为固定值rs。无人机从任务出发点q0∈r2×1出发，以固定高度h飞行，并在最大能量e
max
和最大缓存c
max
的约束下，收集节点信息并返回至q0进行任务卸载和充电工作。
[0142]
1.1传输模型
[0143]
在物联网中，无人机相对于物联网设备的仰角通常较大，且相较于固定的地面设备节点，产生视距(los)通信链路的概率更高。在本发明中，假设无人机空地信道(g2a)主要由los通信链路组成。因此，无人机与节点间的信道模型可以表示为自由空间信道模型，如式(9)所示。
[0144][0145]
其中，为los环境下的单位大尺度衰落，ε为路径损耗指数，在本发明中取ε＝2，表示多径效应引发的小尺度衰落所造成的信道增益，满足dk[n]为第n个时隙时无人机与传感器的直线距离，可以表示为：
[0146][0147]
由于iot设备的通信半径通常在5-100m之间，远远小于无人机所搭载通信设备的通信半径，且无人机只能在物联网设备的通信范围内与之通信。假定无人机可在物联网设
备的通信半径内以传输功率p与所有物联网设备保持稳定通信。在第n个时隙无人机与节点sk的最大传输速率可表示为：
[0148][0149]
其中，b为信号带宽，σ2为加性高斯白噪声(awgn)功率，
[0150]
为了保证无人机可在节点sk的通信范围内的飞行过程中完成信息收集任务和节点sk上传数据的完整性，规定以下约束：
[0151][0152][0153][0154][0155]
式(4)-(7)表示无人机的通信调度约束和iot设备的接入选择约束，其中，αk[n]表示节点sk在第n时隙的通信调度，当αk[n]＝1时，表示无人机正在为节点sk提供信息上传服务，当αk[n]＝0时，表示无人机没有服务于sk；式(5)保证了无人机在节点sk通信范围内的飞行时间多于通信时间，以保证上传数据的完整性，τk表示无人机在节点sk通信范围内的飞行时间；式(6)则限制了无人机在单位时间内可服务的节点个数，即在给定的时隙δ
t
中只为一个节点提供信息收集服务。
[0156]
此外，由于传感器上传信息类型的不同，部分传感器可能需要上传视频、图片、音频等多媒体数据，因此，需要考虑无人机的缓存上限问题即无人机在一次任务中收集的所有节点信息的数据大小应不大于无人机最大缓存上限：
[0157][0158]
其中，表示传感器sk所需上传信息的数据量。
[0159]
1.2飞行策略
[0160]
采用qi∈r2×1和qf∈r2×1表示巡游任务的任务起飞点和降落点，t表示巡游任务完成时间。由于连续时间变量的存在，优化问题中的目标函数和约束条件可能涉及到无穷多变量。因此，本发明采用时间离散化的方法，将巡游任务持续时间[0，t]等分为n个足够小的长度为δ
t
的时间段，其中t＝nδ
t
。当划分的时隙数n足够大时，无人机在每段时隙δ
t
内与传感器节点的距离保持不变，信道增益亦保持不变。用q[n]＝{x[n]，y[n]}∈r2×1表示巡游任务的第n个时隙内无人机的水平投影位置。无人机以固定高度h飞行，除起飞、降落时无人机的垂直速度、加速度变化外，在其他任务时间内是个常量。因此，在本发明中忽略无人机垂直速度和加速度的影响。定义v[n]＝{v
x
[n]，vy[n]}∈r2×1、a[n]＝{a
x
[n]，ay[n]}∈r2×1为无人
机关于水平投影的速度和加速度。因此，可以得到如下所示的无人机加速度、速度和位置之间的关系：
[0161]
v[n]＝v[n-1]+a[n-1]δ
t
，n＝2，
…
，n
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(9)
[0162]
q[n]-q[n-1]＝v[n-1]δ
t
+0.5a[n-1]δ
t2
，n＝2，
…
，n
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(10)
[0163]amin
≤||a[n]||≤a
max
，n＝1，
…
，n
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(11)
[0164]vmin
≤||v[n]||≤v
max
，n＝1，
…
，n
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(12)
[0165]
q[1]＝qi＝q0，q[n]＝qf＝q0ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(13)
[0166]
可以看出，约束(9)-(13)均为关于加速度、速度和位置的线性约束。当时隙δ
t
足够小，无人机相邻时隙之间的轨迹变化可以近似为直线，此时q[n]与q[n-1]之间的距离可由位置表示。式(9)描述了无人机飞行过程中相邻时隙之间的速度约束和加速度约束；式(10)描述了飞行过程中无人机飞行加速度、速度和位置之间的关系；式(11)-(12)规定了无人机的最大加速度和最大速度约束；式(13)则规定了无人机巡游时的起飞、降低点均为初始点。
[0167]
定义o＝{o0，o1，o2，
…
，om，o
m+1
}为设备节点的信息收集顺序，其中m≤k，1≤m≤m，而o0表示无人机起飞地点，o
m+1
表示无人机降落地点。无人机采用多段匀速飞行策略，且假设无人机的加减速过程均在时间ta＝naδ
t
内完成。当无人机完成oi点的信息收集任务后会加速至v
i，i+1
前往下一个需收集信息的节点o
i+1
，并在到达节点o
i+1
的通信边缘时减速至v
i+1
，以保证无人机维持v
i+1
的速度进行节点o
i+1
的信息收集，无人机再次飞行至传感器o
i+1
的通信边缘时即标志着无人机完成节点o
i+1
的信息收集任务，接着无人机加速至v
i+1，i+2
后飞往下一个节点，直至完成全部节点的信息收集任务。
[0168]
其中，v
i，j
表示无人机从节点oi至节点oj的额定速度；vi表示无人机在节点oi通信范围内的额定速度。v1＝{v
0，1
，v
1，2
，
…
，v
m，m+1
}表示系统中无人机在节点之间的额定速度集合，v2＝{v0，v1，
…
，v
m+1
}表示无人机在每个节点通信范围内的额定速度，其中v0＝v
m+1
＝0。
[0169]
依据以上飞行策略，假设节点的通信范围相互不重叠，可用表示无人机在om内的匀速飞行时间，其中τm表示无人机在om内匀速飞行的总时隙数。无人机在收集完节点om的信息后飞至o
m+1
通信边缘的匀速飞行时隙τ
m，m+1
可表示为：
[0170][0171]
其中，由于无人机的加减速都是在额定时间内完成的，因此，无人机的加速度可通过额定速度vi和v
i，j
表示为：
[0172]
[0173]
其中，ftm表示无人机首次抵达节点sk通信边缘的时隙，可以表示为一系列无人机飞行时间的叠加，如下所示：
[0174][0175]
此外，无人机在执行任务中需要进行多次调向或转向，在本发明中不深入无人机调向对信息收集系统的影响，仅设计简单的无人机转向策略即无人机只在传感器正上方或起飞降落点时进行转向，且转向动作可在δ
t
内完成。
[0176]
1.3能耗模型
[0177]
由于无人机携带能量有限，信息收集系统需考虑无人机能耗相关模型，避免无人机在执行任务中能量耗尽带来的不可控因素。通常，无人机的能量消耗包括无人机推进功耗、电路控制功耗和信号收发相关的通信功耗。在实际应用中，无人机的电路控制功耗和通信功耗远小于推进功耗，因此，本发明只考虑推进功耗。在匀速直线飞行中，旋翼无人机的推进能耗模型可近似为与飞行速度相关的表达式如下所示：
[0178][0179]
c1，c2，c3，c4，c5是根据机身阻力、空气密度、旋翼盘面积等信息确定的建模参数，可参考现有研究得出。其中，c1(1+c
2v2
)表示叶片轮廓功率，是旋翼uav的特定术语，用以克服旋翼无人机叶片旋转引起的剖面阻力；表示诱导功率，用以克服无人机在空中飞行的诱导阻力即升力产生的过程中的诱导出来的附加阻力；c
5v3
表示寄生功率，用以克服无人机在空中移动而产生的寄生摩擦力。本发明采用多段匀速飞行策略，因此在一次任务中无人机匀速直线飞行的功耗可表示为多段额定速率(vi、v
i，i+1
)的功耗的叠加，如下所示：
[0180][0181]
无人机在执行任务期间会进行多次加减速，由于无人机加减速在总任务中的时间占比很小，在本发明中将不考虑无人机加减速所造成的能量消耗。此外，考虑无人机的能量限制，为避免无人机出现能量耗尽的情况，规定以下约束：
[0182][0183]
1.4问题提出
[0184]
由于无人机信息收集系统的代价成本的影响因素较多，如与无人机相关的能耗、时间、航程距离、无人机数量等因素以及与传感器相关的电路损耗、通信能耗等因素，因此优化无人机的代价成本具有重要意义。例如，在现有研究中，代价成本定义为如：空中和地面基站的总能耗，也有研究定义为如：无人机数量和任务总时间为系统的代价函数。由于无
人机的能耗成本与无人机运行时间并非成简单的线性关系，为更好得探究多段匀速飞行策略下的无人机信息收集系统的无人机能耗、运行时间之间的关系，本发明将代价函数定义为无人机能耗成本和运行时间成本的函数，即
[0185]
cost
ε
＝εcoste+(1-ε)cost
t
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(20)
[0186]
其中，0≤ε≤1为权衡无人机能耗成本和运行时间成本的加权因子。为无人机能耗成本，其中σe可解释为单位能量的代价，单位可表示为价格/焦耳，e为无人机进行一次任务的能量消耗。cost
t
＝σ
t
t为无人机进行一次任务的运行时间成本。其中，σ
t
可解释为单位时间的代价，单位可表示为价格/秒，t为无人机进行一次任务的运行时间，也可以理解为无人机达到降落点时时间：
[0187][0188]
本发明的目标是在无人机传输、缓存、功率和节点通信半径的限制下，通过联合优化节点采集顺序o、无人机额定速度v1、v2和节点接入选择方案αk[n]以最小化代价函数，该优化问题表述如(p1)所示。
[0189][0190]
s.t.
[0191]
v[n]＝v[n-1]+a[n-1]δ
t
，n＝2，
…
，n
ꢀꢀꢀꢀꢀꢀ
(22a)
[0192][0193]amin
≤||a[n]||≤a
max
，v
min
≤||v[n]||≤v
max
，n＝1，
…
，n
ꢀꢀꢀꢀꢀꢀ
(22c)
[0194]
q[n]-q[n-1]＝v[n-1]δ
t
+0.5a[n-1]δ
t2
，n＝2，
…
，n
ꢀꢀꢀꢀꢀꢀꢀꢀ
(22d)
[0195]
q[1]＝qi＝q0，q[n]＝qf＝q0ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(22e)
[0196][0197][0198][0199][0200]
[0201][0202][0203][0204][0205]
其中，代价函数cost
ε
是一个关于无人机能耗成本coste和任务总时间成本cost
t
的加权函数；约束(22a)-(22e)为无人机执行任务过程中的速度、加速度和位置约束，确保无人机能够在节点间和节点的通信范围内匀速飞行；约束(22f)-(22i)为节点的接入选择约束，确保了无人机能够收集到各节点的完整数据，约束(22j)为无人机缓存约束；约束(22k)为无人机能耗约束；约束(221)-(22m)为无人机各匀速飞行的时间约束；约束(22n)为无人机首次抵达各节点通信半径的时隙约束，确保无人机能准确控制约束(22b)中加减速的时隙。由于约束(22b)为分段函数，αk[n]为二值函数，且约束(22f)、(22k)-(22m)和目标函数均存在非凸函数，问题(p1)很难通过凸优化方法或标准的混合整数线性规划问题解决方法(如分支界定法)求解。
[0206]
2、问题的转化和求解
[0207]
为了求解问题(p1)，先将其转化为带规则凸约束的混合整数问题。然后设计一种基于连续凸逼近的算法来解决此问题。
[0208]
为了解决代价函数coste是一个非凸非凹函数的问题，引入变量cost，将其转化为：
[0209]
cost
ε
≤cost
ꢀꢀꢀꢀꢀꢀ
(23)
[0210]
由于cost
ε
中的仍为非凸项，为了解决这个问题，引入松弛变量ζm、ζ
m，m+1
，表达式如下所示：
[0211][0212][0213]
简化后可以得到：
[0214]
[0215][0216]
此时，目标函数和约束(22k)中的p(vm)、p(v
m，m+1
)可以表示为：
[0217][0218][0219]
由于等式约束条件(22k)、(221)均不是仿射函数，约束集从而不具备凸性。因此，将上述约束条件转化为不等式约束，那么问题(p1)可以转化为问题(p2)：
[0220][0221]
s.t.
[0222]
cost
ε
≤cost
ꢀꢀꢀꢀꢀꢀꢀꢀ
(30a)
[0223][0224][0225][0226][0227]
(22a)-(22k)，(22n)
[0228]
接下来将通过反证法证明问题(p2)和问题(p1)具有相同的最优解。只需证明(30b)-(30e)为问题(p2)的积极约束，即可证明问题(p2)和问题(p1)具有相同的最优解。
[0229]
定理1：问题(p1)与问题(p2)具有相同的最优解集。
[0230]
证明：
[0231]
为证明约束(30b)为问题(p2)的积极约束，假设问题(p2)取最优解时，在其他变量不变的情况下，可以通过降低τm进而降低代价函数cost
ε
的同时保证(30b)等号成立，因此，约束(30b)为问题(p2)的积极约束；假设τ
m，m+1
为问题(p2)的最优解，且约束(30c)满足严格不等式，那么在其他变量不变的情况下，总可以通过减少τ
m，m+1
降低代价函数cost
ε
的同时，使得约束(30c)的等号成立，因此，约束(30c)为问题(p2)的积极约束；同理，在保证问题(p2)的最优解的情况下，约束(30d)和(30e)中的等号成立，否则，ζm或ζ
m，m+1
总是可以不断减小以取得更小的代价函数。因此，(p2)存在使约束(30b)-(30e)满足等式的最优解，并且当约束(30b)-(30e)满足等式时，(p2)与(p1)等价。综上，问题(p1)与问题(p2)具有相同的最优解集。
[0232]
由于约束(22b)为分段函数形式，常规的凸化技巧无法解决此类分段函数。首先，
采用分步线性法将约束(22b)转化如下所示的线性不等式：
[0233][0234][0235][0236][0237]ai，m
∈{0，1}，1≤i≤4，0≤m≤m+1
ꢀꢀꢀꢀꢀꢀꢀꢀ
(31e)
[0238]
接着，为处理“二进制变量
×
连续变量”的函数项a
1，m
(v
m，m+1-vm)，采用大m法对其转化。首先引入变量z
1，1，m
，令
[0239]z1，1，m
＝a
1，m
(v
m，m+1-vm)
ꢀꢀꢀꢀꢀꢀꢀ
(32)
[0240]
假设v
m，m+1-vm的有限上界为m，可以看出，若a
1，m
＝0则z
1，1，m
＝0，当a
1，m
＝1时，z
1，1，m
≤m。因此，可以得到z
1，1，m
≤a
1，m
m。此外，由于z
1，1，m
一直小于v
m，m+1-vm，并且当a
1，m
＝1时z
1，1，m
＝v
m，m+1-vm。因此，函数项a
1，m
(v
m，m+1-vm)可以转化为：
[0241]
0≤z
1，1，m
≤v
m，m+1-vmꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(33)
[0242]z1，1，m
≥v
m，m+1-v
m-(1-a
1，m
)m
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(34)
[0243]
同理，式(31b)-(31d)内其他的“二进制变量
×
连续变量”表示形式的函数项也可采用上述方法进行线性化。
[0244]
接着，引入辅助变量ηm、η
m，m+1
来处理约束(30b)和约束(30c)内的非凸项，使其满足：
[0245][0246][0247]
针对上式中非递减凸函数相乘的形式，采用完全平方公式将其转化为：
[0248][0249][0250]
同样的，针对中的非凸项，引入辅助变量εm、ε
m，m+1
，使其满足：
[0251][0252][0253]
然后采用完全平方公式可转化为：
[0254][0255][0256]
因此，问题(p2)可以转化为问题(p3)：
[0257][0258]
s.t.
[0259][0260][0261][0262]
(22a)，(22c)-(22k)，(22n)，(30a)，(30d)-(30e)，
[0263]
(31a)-(31e)，(37)-(38)，(41)-(42)
[0264]
可以看出，由于约束(22f)中非凸项的存在，问题(p3)仍然是非凸的。由于任意可微凸函数的一阶泰勒展开都是函数的全局下界，而(22f)中rk[n]相对于是凸的，因此，可以将其作为整体部分处理，采用逐次凸逼近(sca)技术，通过迭代法解决该问题。对于第r次迭代的局部最优值qr[n]，通过一阶泰勒展开可以得到下界
[0265][0266]
其中，
[0267][0268][0269]
接下来处理约束(22f)中的乘积项αk[n]rk[n]，由于αk[n]rk[n]是“二进制变量
×
连续变量”的形式。引入辅助变量γk[n]，使其满足γk[n]＝αk[n]rk[ftk+τi]。接着采用大m法将其转化为如下约束：
[0270]
0≤γk[n]≤rk[ftk+τi]
ꢀꢀꢀꢀꢀꢀꢀ
(47)
[0271]
γk[n]≥rk[ftk+τi]-(1-αk[n])m
ꢀꢀꢀꢀꢀ
(48)
[0272]
由于平方项ζ
m2
在的处的一阶泰勒展开的右侧为仿射函数，符合凸优化规则。因此，分别对(23f)和(23f)中的平方项进行一阶泰勒展开，如下所示：
[0273][0274][0275]
由于(37)中存在两个凸函数之差(dc)的结构，导致(p3)仍然是非凸的。可以看到第r次迭代时，在点处的一阶泰勒展开：
[0276][0277]
接着，引入辅助变量μ
1，m
，使得并将中按照式(51)中的方式进行展开，可以得到：
[0278][0279]
式(52)可进一步简化为：
[0280][0281]
同样的，针对与式(37)结构相似的式(38)和式(41)-(42)，可以得到：
[0282][0283][0284][0285]
因此，问题(p3)可以根据任意局部点qr[n]、[n]、p(vm)r、和p(v
m，m+1
)r及其下界表达式近似为带有迭代值的问题(p4)：
[0286][0287]
s.t.
[0288]
(22a)，(22c)-(22e)，(22g)-(22k)，(22n)，(30a)，
[0289]
(31a)-(31e)，(43a)-(43c)，(44)，(47)-(50)，(53)-(56)
[0290]
由于问题(p4)是一个带有整数优化变量的midcp问题，可以通过cvx和gurobi求解
器联合解决。因此，可以采用sca技术通过连续迭代的方式优化问题(p4)，求解(p4)的sca方法如算法1所示。由于问题(p4)采用一阶泰勒展开的下界近似(p1)中的约束，这就意味着问题(p1)可以得到有效解决，并且(p1)满足kkt条件。因此，可以保证nafs算法的收敛性。算法1的计算复杂度可由算法的迭代次数和每次迭代的更新变量数计算求得o(r(9m+4mn)3)。
[0291]
为便于描述，定义a＝{o，v1，v2，cost，αk[n]，τm，τ
m，m+1
，μ
1，m
，μ
2，m
，p(vm)，p(v
m，m+1
)}为解空间。
[0292][0293]
3、仿真结果与分析
[0294]
为验证所提算法的有效性，利用cvx工具包和gurobi求解器进行性能仿真。仿真场景一个1000
×
1000m2的二维区域内，区域内随机分布k＝10个iot节点，无人机的出发点和终点设置为qi＝qf＝q0＝[0，0]，单位为m。其次，假设无人机的缓存容量和能源限制分别为c
max
＝1.2gb和e
max
＝1.15mj，并且无人机的飞行高度固定在h＝100m。接着，将无人机能耗的相关参数c1
，
c2，c3，c4，c5分别设置为580.65、4.6875
×
10-4
、790.6715、14.4364和0.0312。表1总结了无人机飞行和通信相关参数。
[0295]
表1无人机飞行和通信相关参数
[0296]
参数数值离散化时间单位δ
t
1s无人机最大速度v
max
30m/s无人机最大加速度a
max
15m/s2无人机单次加速时间ta2s通信带宽b0.3mhz加性高斯白噪声功率σ
2-110dbm/hz单位信道功率增益β
0-60dbiot设备的发射功率p0.1wiot设备的通信半径rs50m单位能量代价σe500price/j单位时间代价σ
t
1price/s
[0297]
首先，为10个iot设备设置不同的数据量[40 40 30 100 70 50 80 50 30 40]，单位均为mb，研究nafs算法的三种不同加权因子ε的代价函数的收敛性，如图2所示。可以看到，ε＝1的代价函数即最小功耗、ε＝0.5的代价函数和ε＝0的代价函数即最小任务时间都在随着迭代次数的增加而迅速下降，并在十数次迭代中收敛。此外，还能看出ε＝0的代价函
数的收敛速度快于另外两种方案，其原因在于ε＝0时，无人机信息收集系统忽略了无人机能耗的影响，进而加速了算法的运算速度。
[0298]
接着，验证nafs算法ε＝0.5时无人机的飞行轨迹、速度和iot设备的接入选择方案，如图3和图4所示。图三展示了无人机从始发点[0，0]开始，途径10个iot设备并收集其数据后返回终点[0，0]的过程，期间无人机采用直线飞行。图4展示了无人机多段匀速策略与iot设备接入方案的匹配程度，仿真结果与本发明的预期高度吻合。可以看到当无人机即将进入iot设备的通信半径时，会减速至额定速度并保持匀速飞行，其减速后匀速飞行的时间正好为iot设备接入时间，能够保证无人机收集到iot设备中的完整数据，收集完数据后无人机会调整至最优速度后飞向下一个节点。
[0299]
其次，探究nafs算法下无人机速度、任务总时间和能耗之间的关系。无人机能耗和速率随代价加权因子ε的变化曲线如图5所示，随着加权因子ε的不断增加，无人机能耗和速率逐渐降低。这方面的原因有两点，其一是当v＞10后，无人机的功耗与速率大体是成正比的，如图5中右上角无人机速率和功率之间的变化曲线图所示；其二是由于加权因子ε的变化，使得代加函数cost
ε
中功率的占比不断加大，算法会在增加任务总时间的情况下进一步降低功耗，这一点在图6中的体现更为明显。值得注意的是，在ε＝0.8以后，能耗有着轻微幅度的增加，这在图5和图6中都能看出。这是因为与速度相关的无人机功率远大于每段匀速时间，速度小幅度的减少而带来的功率的变化对代价函数的影响远大于时间的变化对代价函数的影响，从而降低了任务总时间对代价函数的影响程度。因此，当ε＞0.6时，适当增加任务时间在代价函数中的占比时会增加匀速时间对代价函数的影响程度，减轻速度轻微变化对代价函数的影响，进而可以得到更优的无人机最小功耗方案。
[0300]
最后，对本发明所提算法的性能进行了评估。对比了nafs算法与另外两种飞行策略的无人机能耗和任务总时间。第一种算法是基于悬停策略的无人机信息收集(hs)方法
[23]
，无人机的飞行速度维持在30m/s，悬停位置为节点的正上方；第二种算法是基于匀速飞行策略的无人机信息收集(uvs)方法，无人机飞行速度是保证全部节点数据收集完整性的最大速度。在图7中，可以看到采用hs和uvs算法的无人机信息收集方案的能耗远高于采用采用hafs算法的无人机收集方案。原因在于随着数据量的不断增大，在传输速率不增的情况下，无人机与各iot设备的通信时间也会不断增加，悬停时间或匀速飞行时间亦随之增加，进而增加无人机的能耗，由于hafs算法是针对无人机的飞行速度进行多段匀速优化，因此在保证数据收集完整性的同时进一步降低系统能耗，减少任务总时间。此外，在图8中也能看到不同ε情况下多段匀速飞行策略随数据量的变化，当ε＝0.8时无人机的飞行能耗略微低于ε＝1时的功耗，这与图5和图6的数据表现不谋而合。
[0301]
图9展示了无人机总任务时间随iot设备数据量的变化曲线。其中，uvs算法更偏向于小数据量信息收集系统的能耗优化，在数据量小于40mb时无人机的能耗较小，但其在数据量大于50mb后的能耗呈指数上升并且系统总任务时间超过400s。hs算法则是一个偏向于时间优化的算法，可以在图9中看到，其任务时间的优化表现很好，但仍略差于ε＝0时的nafs算法，且在小数据量的信息收集系统，hs算法的能耗表示相对ε＝0时的nafs算法差距很大。
[0302]
本领域普通技术人员可以理解：附图只是一个实施例的示意图，附图中的流程并不一定是实施本发明所必须的。