一种图像空域加密和解密的方法

1.本发明涉及一种改进的基于logistic混沌映射的加密方法，用于图像空域加密，具体涉及一种基于改进的logistic混沌映射与warnsdorff规则置乱二次预测反馈的图像空域加密方法。


背景技术：

2.数字图像是一种被广泛采用的数据格式，因具有快捷方便、信息量大等特点，其在各个领域都具有广泛的应用。随着数字图像的广泛应用，尤其是在网络环境下的图像数据的传输，使得数字图像的安全保护变得越来越重要。对图像进行安全保护最直接的方法就是对图像数据进行加密。
3.互联网技术的发展为我们提供了跨区域进行数据传输的通道，尤其是近年来4g/5g技术的发展使得图像、视频数据在网络上自由传输成为可能。由于图像或视频数据在网络中、尤其是在无线网络中进行传输时，很容易被非法截取，所以人们对图像、视频等多媒体数据传输的安全性提出了很高的要求。保证数据安全传输的最直接方法就是对数据进行加密，所以有关图像、视频等媒体的加密算法应运而生，并且近年来得到迅速发展。
4.混沌系统具有初始条件敏感性、遍历性和混合性等优点，符合密码学要求，所以近年来，基于混沌理论的数字图像空域加密方案取得了飞速发展。基于骑士巡游置乱的图像加密算法因密钥空间大，能够抵抗穷尽攻击，密钥敏感性强等特点在近年得到了学术界的广泛关注与研究。
5.一、logistic混沌映射混沌源于非线性动力系统，是一个任意随时间变化的过程，这个过程是确定性的、类似随机的、非周期的，并且对于初始值有极敏感的依赖性。这些特性正符合序列密码的要求，所以混沌常常用于数据的加密过程中。logistic映射是研究动力系统、混沌、分形等复杂系统行为的一个经典模型，其由于原理简单、计算方便而被广泛应用于加密领域。一维logistic映射数学表达式描述为：在上式中μ∈(0,4]被称为logistic参数，当x∈(0,1)时，logistic映射处于混沌状态，也就是说，初始条件x0∈(0,1)在logistic映射迭代作用下产生的序列是非周期的、不收敛的。并且当x0或参数μ发生微小变化时，在logistic映射迭代作用下产生的序列迥异。
6.二、基于logistic混沌映射的数据加密设定初始参数μ和x0，计算logistic映射迭代得到混沌集x={x0, x1, x2,
ꢀ…
, xn-1}，其中xi∈（0,1）。对x进行运算：，得到集合h={ h0, h1, h2,
ꢀ…
, hn-1}。针对数据流d={d0, d1, d2,
ꢀ…
, dn-1}，进行与h的异或运算，得到数据流d的密文e ={e0, e1, e2,
ꢀ…
, en-1}。对密文e再与h做异或运算，得到数据流原文d。在此
我们称初始参数μ和x0为密钥，基于logistic映射迭代产生的混沌序列，实现了对数据流的对称加密。
7.但是，经典logistic 映射存在系统参数范围受限、混沌序列分布不均等问题。
8.三、骑士巡游问题与warnsdorff规则骑士巡游问题是图论的一个经典问题。国际象棋的棋盘为m
×
n的方格棋盘，现将骑士（马）放在任意指定的方格中，按照骑士走棋的规则（同中国象棋，马走日字）进行移动，要求每个方格只能进入一次，最终使得骑士能够走遍棋盘的每个方格，这就是骑士巡游问题。对于m
×
n的方格棋盘，当骑士走遍棋盘的每个方格时，其巡游路径是无序的，我们可以根据骑士的巡游顺序将待加密图像的像素或空间子块进行重新排序，从而达到对图像信息进行隐藏的目的，达到加密的效果，我们通常称之为图像的置乱。目前，基于骑士巡游置乱的图像加密算法因密钥空间大，能够抵抗穷尽攻击，密钥敏感性强等特点在近年得到了学术界的广泛关注与研究。
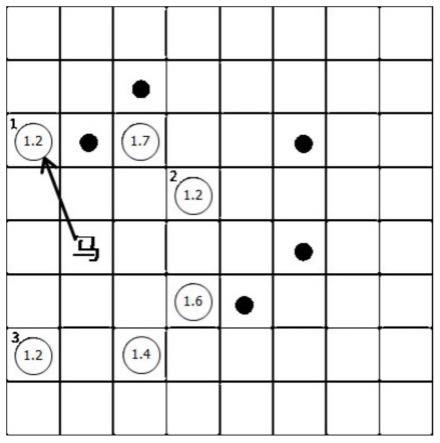
9.一般情况下，由于骑士在棋盘中的起始位置任意，在移动规则限制的条件下，若按照规则随意移动，很难能够走遍棋盘的每个方格。最经典的解决跳马问题的算法是德国数学家h.c. warnsdorff在1823 年发明的算法，称作warnsdorff规则。warnsdorff规则的主要思想是从开始位置起进行移动时，不能冒然将骑士移动到某一候选位置，而是要对所有的候选位置进行预测和判断，找出最优的候选位置进行移动。warnsdorff规则认为最优的候选位置是以所有的候选位置为起始点，进行下一步移动，下一步移动的候选位置最少的点，即为最优的候选位置点。这种方法我们称之为预测反馈，如图1所示。
10.图1所示的是骑士巡游的第 10 步的情况：从骑士当前位置（马字所在位置）移动，可能有三个位置可移动，即
②
、
⑤
、
⑥
所在的方格。在方格中显示的数字为本方格作为起始位置时，下一步可移动的候选位置的个数。此时，我们选择下一步可移动的候选位置的个数最少的作为最优候选位置。显然，第十步应该跳到
②
所在的位置。warnsdorff算法并不是对所有情况都有效，当棋盘大于76
×
76 时，这种算法就无效了。


技术实现要素：

11.为解决经典logistic 映射在系统参数范围受限、混沌序列分布不均的问题，本发明提供一种基于改进的logistic混沌映射与warnsdorff规则置乱二次预测反馈的图像空域加密方法。
12.本发明的技术方案：一种图像空域加密和解密的方法，图像加密方法包括以下步骤：（1）建立logistic混沌序列 z = {z0, z1,
ꢀ…
, z
n-1
}；（2）利用warnsdorff规则的二次预测反馈算法对16
×
16棋盘进行遍历，以棋盘位置为起始点，得到遍历路径并转换为一维数组；（3）对图像数据加密；（4）图像数据密文置乱。
13.优选的，图像解密方法包括以下步骤：（1）建立logistic混沌序列 z = {z0, z1,
ꢀ…
, z
n-1
}；（2）利用warnsdorff规则的二次预测反馈算法对16
×
16棋盘进行遍历，以棋盘位
置为起始点，得到遍历路径并转换为一维数组；（3）图像数据反置乱；（4）图像数据解密。
14.优选的，图像加密方法步骤中，建立logistic混沌序列 z = {z0, z1,
ꢀ…
, z
n-1
}步骤之前还包括以下步骤：将图像像素按照行序列转换为一维数组形式，每个像素r、g、b分量作为一维数组的一个元素；设有某图像 d=m
×
l，m为高，l为图像的宽，按照以上原则，图像d就可以表示为{r0， g0， b0， r1， g1， b1，
……
, r m
×
l-1
， g m
×
l-1
， b m
×
l-1
}，为了计算方便，在此设d={d0, d1,
ꢀ…
, d
k-1
},其中k为图像像素数的3倍，k= m
×
l
×
3。
15.优选的，logistic混沌序列 z包括以下步骤：（a）、设定参数x0，μ，delay，cycle，multipower，bitswap；（b）、根据 xn=x
n-1
*μ*(1-x
n-1
)，进行混沌序列迭代计算；（c）、经过delay次迭代后，取稳定的混沌序列，序列长度为cycle，得到混沌序列x={x0, x1,
ꢀ…
, x
n-1
}， n=cycle；（d）、对于获取的混沌序列x，计算 （x* multipower）%256，得到字节混沌序列h={h0, h1,
ꢀ…
, h
n-1
}；（e）、对h序列逐元素hi进行移位操作，根据元素序号i%3的值，进行1827、1234或1526位交换操作；若i%3==0，则对hi进行1827位交换操作；若i%3==1，则对hi进行1234位交换操作；若i%3==2，则对hi进行1526位交换操作；（f）根据bitswap对h序列逐元素hi再次进行移位操作，若bitswap==0，则对hi进行1827位交换操作；若bitswap==1，则对hi进行1234位交换操作；若bitswap==2，则对hi进行1526位交换操作。
16.优选的，步骤（2）对16
×
16棋盘进行遍历，以棋盘位置（0， 0），（7，7），（15，15）为起始点，得到遍历路径并转换为一维数组，记为w00[256]、w77[256]、w1515[256]；warnsdorff规则的二次预测反馈算法：采用二次预测反馈算法，即经过一次预测获得的下一步移动候选位置点数相同时，启动二次预测，预测的方法与一次预测相同：以多个最少候选位置点为起始点，进行再次移动预测，将二次移动预测的候选位置点数相加，得到二次预测候选位置点之和；选择二次预测候选位置点之和最小的一次预测最少候选位置点作为移动点。
[0017]
优选的，图像数据行加密步骤包括：对于待加密的图像数据序列d={d0, d1,
ꢀ…
, d
k-1
}，按照数据序列和混沌序列的序号进行对应元素异或操作，实现对图像数据的加密，得到数据序列的密文e={e0, e1,
ꢀ…
, e
k-1
}，即即e
i =diz
i%n
，其中i=0,1,
…
,k-1；对于图像数据密文序列e={e0, e1,
ꢀ…
, e
k-1
}，按照每256元素进行分组，得到k/256个 e分组，记为e
t
，t=0,1,
…
, k/256-1；当t%3=0时，利用w00[256]进行置乱，当t%3=1时，利用w77[256]进行置乱，当t%3=2时，利用w1515[256]进行置乱；得到的e-scrambling即为图像数据的最终加密序列。
[0018]
优选的，图像数据反置乱步骤包括：
对于图像数据密文置乱序列e-scrambling，按照每256元素进行分组，得到k/256 个 e-scrambling分组，记为e-s
t
，t=0,1,
…
, k/256-1；当t%3=0时，利用w00[256]进行反置乱，当t%3=1时，利用w77[256]进行反置乱，当t%3=2时，利用w1515[256]进行反置乱；进行反置乱操作后，得到图像数据的加密序列e；图像数据解密步骤包括：对于加密的图像数据序列e={e0, e1,
ꢀ…
, e
k-1
}，按照数据序列和混沌序列的序号进行对应元素异或操作，实现对数据的解密，得到数据序列的明文d={d0, d1,
ꢀ…
, d
k-1
}，即 即 d
i =eiz
i%n
,i=0,1,
…
,k-1。
[0019]
优选的，将基于warnsdorff规则的二次预测反馈算法生成的骑士巡游序列转换为一维数组形式，记为 w[16
×
16]={w0， w1，
……
, w
254
， w
255
}，利用w[16
×
16]对图像 d={ d0, d1,
ꢀ…
, d
k-1
}进行置乱和反置乱；置乱算法：d-scrambling[i] = d[(i/256)*256+w[i%256]]，i=0，1，
…
, k-1；每分组的置乱算法如下：e
t-scrambling[i] = e
t
[w[i]]，t=0,1,
…
, k/256-1;i=0,1,
…
,255；反置乱算法：d[(i/256)*256+w[i%256]] = d-scrambling[i]，i=0，1，
…
, k-1；每分组的反置乱算法如下：e
t
[w[i]] = e-s
t [i]，t=0,1,
…
, k/256-1; i=0,1,
…
,255。
[0020]
优选的，x0：初始值，取值范围为（0，1）；μ：logistic参数，取值范围（0，4]；delay：延时，等待混沌序列稳定经过的迭代次数；cycle：周期，指获取的混沌序列的长度；multipower：倍率，是由小数混沌序列计算字节混沌系列时的倍率；bitswap：位交换算法，提供三种交换算法：1827交换算法、1234交换算法、1526交换算法 。
[0021]
优选的，x0取值0.5438125；μ：取值3.9438125；delay：取值100；cycle：取值256；multipower：取值106；1827交换算法：将字节的第一位第八位交换、第二位第七位交换、第三位第六位交换、第四位第五位交互，生成新的字节；1234交换算法：将字节的第一位第二位交换、第三位第四位交换、第五位第六位交换、第七位第八位交互，生成新的字节；1526交换算法：将字节的第一位第五位交换、第二位第六位交换、第三位第七位交换、第四位第八位交互，生成新的字节。
[0022]
本发明的有益效果：本方法扩展了logistic混沌映射的生成参数并对生成的混沌序列进一步进行了位交换，增强了其伪随机性。本方法通过二次预测反馈的warnsdorff规则生成了16
×
16块置乱序列，对图像数据进行流式置乱。本方法根据生成的logistic混沌序列和warnsdorff16
×
16块置乱序列，提出了完整的图像加密算法。具体表现在以下几个方面：1、利用混沌映射导出离散混沌加密序列，对其进行放大取模后再进行位交换操作，增强其伪随机性。
[0023]
2、扩展初始参数，增强产生混沌序列的机密性。
[0024]
3、采用基于warnsdorff规则的二次预测反馈算法生成三个置乱序列，分别对密文
进行置乱，增强了置乱的机密性。
[0025] 4、对数字图像进行连续行置乱，以最大可能消除方块效应。
附图说明
[0026]
图1为骑士巡游的第 10 步的情况图；图2为1827位交换算法图；图3为1234位交换算法图；图4为1526位交换算法图；图5为选择下一步的移动候选点数目最少的1.2点作为本次移动的目标点图；图6为对各个移动候选点进行一次预测得到的下一步的候选点数目图；图7为对预测图；图8为对的预测图；图9为对的预测图；图10为选择二次预测候选点之和为9的点作为本次移动的目标点图；图11为初始位置在（0，0）位置的骑士遍历路径图；图12为初始位置在（7，7）位置的骑士遍历路径图；图13为初始位置在（15，15）位置的骑士遍历路径图。
具体实施方式
[0027]
一、logistic混沌序列生成参数基于logistic混沌映射生成混沌序列，初始参数设定为：x0：初始值，取值范围为（0，1），在此取值（不限于）0.5438125。
[0028]
μ：logistic参数，取值范围（0，4]，在此取值（不限于）3.9438125。
[0029] delay：延时，等待混沌序列稳定经过的迭代次数，在此取值（不限于）100。
[0030]
cycle：周期，指获取的混沌序列的长度，在此取值（不限于）256。
[0031]
multipower：倍率，在此取值（不限于）106，是由小数混沌序列计算字节混沌系列时的倍率。
[0032]
bitswap：位交换算法，提供三种交换算法：1827交换算法、1234交换算法、1526交换算法 。
[0033]
二、位交换算法 提供三种位交换算法，待选对混沌系列的每一元素进行位交换操作。
[0034]
1、1827位交换算法（见图2）将字节的第一位第八位交换、第二位第七位交换、第三位第六位交换、第四位第五位交互，生成新的字节。
[0035]
2、1234位交换算法（见图3）将字节的第一位第二位交换、第三位第四位交换、第五位第六位交换、第七位第八位交互，生成新的字节。
[0036]
3、1526位交换算法（见图4）
将字节的第一位第五位交换、第二位第六位交换、第三位第七位交换、第四位第八位交互，生成新的字节。
[0037]
三、logistic混沌序列生成过程1、设定参数x0，μ，delay，cycle，multipower，bitswap2、根据 xn=x
n-1
*μ*(1-x
n-1
)，进行混沌序列迭代计算，以x0为初始值进行迭代计算；3、经过delay次迭代后，取稳定的混沌序列，序列长度为cycle，得到混沌序列x={x0, x1,
ꢀ…
, x
n-1
}， n=cycle。
[0038]
4、对于获取的混沌序列x，计算 （x* multipower）%256，得到字节混沌序列h={h0, h1,
ꢀ…
, h
n-1
}；h
0=
（x0* multipower）%256，h
n-1
=（x
n-1
* multipower）%256；5、对h序列逐元素hi进行移位操作，根据元素序号i%3的值，进行1827、1234或1526位交换操作。若i%3==0，则对hi进行1827位交换操作；若i%3==1，则对hi进行1234位交换操作；若i%3==2，则对hi进行1526位交换操作。
[0039]
6、根据bitswap对h序列逐元素hi再次进行移位操作，若bitswap==0，则对hi进行1827位交换操作；若bitswap==1，则对hi进行1234位交换操作；若bitswap==2，则对hi进行1526位交换操作。
[0040]
7、得到最终的logistic混沌序列 z = {z0, z1,
ꢀ…
, z
n-1
}。
[0041]
四、图像数据利用生成的logistic混沌序列加密和解密过程1、图像数据一维化：将图像像素按照行序列转换为一维数组形式，每个像素r、g、b分量作为一维数组的一个元素。设有某图像d（m
×
l），m为高，l为图像的宽，按照以上原则，图像d就可以表示为{r0， g0， b0， r1， g1， b1，
……
, r m
×
l-1
， g m
×
l-1
， b m
×
l-1
}2、加密过程：为计算方便，将d={r0， g0， b0， r1， g1， b1，
……
, r m
×
l-1
， g m
×
l-1
， b m
×
l-1
}表示为d={d0, d1,
ꢀ…
, d
k-1
}，k=m
×
l
×
3。
[0042]
对于待加密的图像数据序列d={d0, d1,
ꢀ…
, d
k-1
}，按照数据序列和混沌序列的序号进行对应元素异或操作，实现对图像数据的加密，得到数据序列的密文e={e0, e1,
ꢀ…
, e
k-1
}，即即e
i =diz
i%n
，其中i=0,
…
,k-1。
[0043]
3、解密过程：对图像数据序列的密文e={e0, e1,
ꢀ…
, e
k-1
}，按照数据序列和混沌序列的序号进行对应元素异或操作，实现对图像数据的解密，得到数据序列的原文d={d0, d1,
ꢀ…
, d
k-1
}，即ez=d，即d
i =eiz
i%n
，其中i=0,
…
,k-1。
[0044]
五、warnsdorff规则的二次预测反馈算法warnsdorff规则的主要思想是从开始位置起进行移动时，不能冒然将骑士移动到某一候选位置，而是要对所有的候选位置进行预测判断，找出最优的候选位置进行移动。warnsdorff规则认为最优的候选位置是以所有的候选位置为起始点，进行下一步移动，下一步移动的候选位置最少的点，即为最优的候选位置点。这种方法我们称之为预测反馈。而在实际的操作中，经过一次预测获得的下一步移动最少候选位置点数可能多于一个，此时
一般的处理方式是任选一个，或者选择距棋盘中心位置最远的点，但是这种选择具有不确定性，可能会导致巡游遍历的失败。本发明采用二次预测反馈算法，即经过一次预测获得的下一步移动候选位置点数相同时，启动二次预测，预测的方法与一次预测相同：以多个最少候选位置点为起始点，进行再次移动预测，将二次移动预测的候选位置点数相加，得到二次预测候选位置点之和。此时，选择二次预测候选位置点之和最小的一次预测最少候选位置点作为移动点。这个过程如下。
[0045]
图5中，一次预测的各个移动候选点的下一步移动候选点数目各不相同，选择下一步的移动候选点数目最少的1.2点作为本次移动的目标点。图5中的1.2、1.7等各编号，第一个数字表示预测次数，第二个数字表示一次预测的候选位置点数。
[0046]
但是，如图6所示，棋盘中的黑点表示已经占用的点，此时对各个移动候选点进行一次预测得到的下一步的候选点数目有的相同。图6中有三个位置的下一步移动候选点数目均为2，并且2为下一步移动候选点数目的最小值，此时一次预测失效，需要进行二次预测。
[0047]
对的预测如图7所示，在图中1.2.2、1.2.7表示1.2的两个候选移动点，最后一位数字2、7表示对二次预测的移动候选点数。有两个移动候选点，二次预测的两个移动候选点的下一步移动候选点数分别为2和7，之和为9。
[0048]
对的预测如图8所示，本点有两个移动候选点，二次预测的两个移动候选点的下一步移动候选点数分别为5和7，之和为12。
[0049]
对的预测如图9所示，本点有两个移动候选点，二次预测的两个移动候选点的下一步移动候选点数分别为3和7，之和为10。
[0050]
此时，由于三个一次预测的候选点数最小且相同的点的二次预测候选点之和分别为9、12和10，此时选择二次预测候选点之和为9的点作为本次移动的目标点，见图10。
[0051]
设定16
×
16棋盘和骑士的初始位置，利用warnsdorff规则的二次预测反馈算法对棋盘进行遍历，在棋盘网格位置记录移动的步数。
[0052]
图11是初始位置在左上角，即（0，0）位置的骑士遍历路径。
[0053]
图12是初始位置在右下角，即（7，7）位置的骑士遍历路径。
[0054]
图13是初始位置在（15，15）位置的骑士遍历路径。
[0055]
六、骑士巡游序列对图像数据的行置乱方法将基于warnsdorff规则的二次预测反馈算法生成的骑士巡游序列转换为一维数组形式，记为 w[16
×
16]={w0， w1，
……
, w
254
， w
255
}，利用w[16
×
16]对图像 d={ d0, d1,
ꢀ…
, d
k-1
}进行置乱和反置乱。
[0056]
1、置乱算法d-scrambling[i] = d[(i/256)*256+w[i%256]]，i=0，1，
…
, k-1。
[0057]
2、反置乱算法d[(i/256)*256+w[i%256]] = d-scrambling[i]，i=0，1，
…
, k-1。
[0058]
七、本发明的图像空域加密步骤1、将图像像素按照行序列转换为一维数组形式，每个像素r、g、b分量作为一维数
组的一个元素。设有某图像 d（m
×
l），m为高，l为图像的宽，按照以上原则，图像d就可以表示为{r0， g0， b0， r1， g1， b1，
……
, r m
×
l-1
， g m
×
l-1
， b m
×
l-1
}，为了计算方便，在此设d={d0, d1,
ꢀ…
, dk-1},其中k为图像像素数的3倍，k= m
×
l
×
3。
[0059]
2、设定参数x0，μ，delay，cycle，multipower，bitswap3、根据 xn=x
n-1
*μ*(1-x
n-1
)，进行混沌序列迭代计算。
[0060]
4、经过delay次迭代后，取稳定的混沌序列，序列长度为cycle，得到混沌序列x={x0, x1,
ꢀ…
, x
n-1
}， n=cycle。
[0061]
5、对于获取的混沌序列x，计算 （x* multipower）%256，得到字节混沌序列h={h0, h1,
ꢀ…
, h
n-1
}。
[0062]
6、对h序列逐元素hi进行移位操作，根据元素序号i%3的值，进行1827、1234或1526位交换操作。若i%3==0，则对hi进行1827位交换操作；若i%3==1，则对hi进行1234位交换操作；若i%3==2，则对hi进行1526位交换操作。
[0063]
7、根据bitswap对h序列逐元素hi再次进行移位操作，若bitswap==0，则对hi进行1827位交换操作；若bitswap==1，则对hi进行1234位交换操作；若bitswap==2，则对hi进行1526位交换操作。
[0064]
8、得到最终的logistic混沌序列 z = {z0, z1,
ꢀ…
, z
n-1
}。
[0065]
9、利用warnsdorff规则的二次预测反馈算法对16
×
16棋盘进行遍历，以棋盘位置（0， 0），（7，7），（15，15）为起始点，得到遍历路径并转换为一维数组，记为w00[256]、w77[256]、w1515[256]。
[0066]
9、图像数据行加密。
[0067]
对于待加密的图像数据序列d={d0, d1,
ꢀ…
, d
k-1
}，按照数据序列和混沌序列的序号进行对应元素异或（）操作，实现对图像数据的加密，得到数据序列的密文e={e0, e1,
ꢀ…
, e
k-1
}，即dz=e,即e
i =diz
i%n
，其中i=0,1,
…
,k-1。
[0068]
10、图像数据密文置乱。
[0069]
对于图像数据密文序列e={e0, e1,
ꢀ…
, e
k-1
}，按照每256元素进行分组，得到k/256个 e分组，记为e
t
，t=0,1,
…
, k/256-1。当t%3=0时，利用w00[256]进行置乱，当t%3=1时，利用w77[256]进行置乱，当t%3=2时，利用w1515[256]进行置乱。
[0070]
每分组的置乱算法如下：e
t-scrambling[i] = e
t
[w[i]]，t=0,1,
…
, k/256-1;i=0,1,
…
,255；得到的e-scrambling即为图像数据的最终加密序列。
[0071]
八、本发明的图像空域解密步骤1、设定参数x0，μ，delay，cycle，multipower，bitswap，与加密算法中一致。
[0072]
2、根据 xn=x
n-1
*μ*(1-x
n-1
)，进行混沌序列迭代计算。
[0073]
3、经过delay次迭代后，取稳定的混沌序列，序列长度为cycle，得到混沌序列x={x0, x1,
ꢀ…
, x
n-1
}， n=cycle。
[0074]
4、对于获取的混沌序列x，计算 （x* multipower）%256，得到字节混沌序列h={h0, h1,
ꢀ…
, h
n-1
}。
[0075]
5、对h序列逐元素进行hi移位操作，根据元素序号i%3的值，进行1827、1234或1526
位交换操作。若i%3==0，则对hi进行1827位交换操作；若i%3==1，则对hi进行1234位交换操作；若i%3==2，则对hi进行1526位交换操作。
[0076]
6、根据bitswap对h序列逐元素hi再次进行移位操作，若bitswap==0，则对hi进行1827位交换操作；若bitswap==1，则对hi进行1234位交换操作；若bitswap==2，则对hi进行1526位交换操作。
[0077]
7、得到最终的logistic混沌序列 z = {z0, z1,
ꢀ…
, z
n-1
}。
[0078]
8、利用warnsdorff规则的二次预测反馈算法对16
×
16棋盘进行遍历，以棋盘位置（0， 0），（7，7），（15，15）为起始点，得到遍历路径并转换为一维数组，记为w00[256]、w77[256]、w1515[256]。
[0079]
9、图像数据反置乱。
[0080]
对于图像数据密文置乱序列e-scrambling，按照每256元素进行分组，得到k/256 个 e-scrambling分组，记为e-s
t
，t=0,1,
…
, k/256-1。当t%3=0时，利用w00[256]进行反置乱，当t%3=1时，利用w77[256]进行反置乱，当t%3=2时，利用w1515[256]进行反置乱。
[0081]
每分组的反置乱算法如下：e
t
[w[i]] = e-s
t [i]，t=0,1,
…
, k/256-1; i=0,1,
…
,255；进行反置乱操作后，得到图像数据的加密序列e。
[0082]
10、图像数据解密。
[0083]
对于加密的图像数据序列e={e0, e1,
ꢀ…
, e
k-1
}，按照数据序列和混沌序列的序号进行对应元素异或（）操作，实现对数据的解密，得到数据序列的明文d={d0, d1,
ꢀ…
, d
k-1
}，即ez=d, 即 d
i =eiz
i%n
,i=0,1,
…
,k-1。
[0084]
以上所述，仅是本发明的较佳实施例而已，并非对本发明作任何形式上的限制，虽然本发明已以较佳实施例揭示如上，然而并非用以限定本发明，任何本领域技术人员，在不脱离本发明技术方案范围内，当可利用上述揭示的技术内容做出些许更动或修饰为等同变化的等效实施例，但凡是未脱离本发明技术方案内容，依据本发明的技术实质对以上实施例所作的任何简介修改、等同变化与修饰，均仍属于本发明技术方案的范围内。