一种基于高阶累积量和累积分布函数的调制识别方法与流程

1.本发明属于软件无线电中的自动调制识别技术领域，具体涉及一种基于高阶累积量和累积分布函数的调制识别方法。


背景技术：

2.调制识别是指在电子侦察等非协作通信中，接收端根据一定的算法判断出截获信号调制方式的技术。不同的场合，待识别信号的调制集是不同的，一般是已知信号调制集合，然后通过调制识别技术判断出待识别信号是集合中的哪一种。
3.本发明的识别对象是{qpsk/4qam，8psk，16psk，16qam，64qam}中的一种，其星座图如图1所示。当信号经过了平坦衰落信道后，除了含有高斯白噪声，还会存在未知的相位旋转，如图2所示。当存在相位旋转时，4qam信号和qpsk信号在本质上是一样的，归为一类信号。
4.对于上述信号，fanggang wang and xiaodong wang.fast and robust modulation classification via kolmogorov-smirnov test[j].ieee transactions on communications,2010,58(8):2324-2332给出了三种基于k-s检验的识别方法，分别是基于幅度的k-s检验，基于正交的k-s检验和基于相位的k-s检验。其基本原理是计算出待识别信号的幅度、相位或其他某一特征，然后统计该特征的累积分布函数，并将这一分布函数跟每一种可能的调制信号的经验分布函数进行匹配，匹配度最高的就是识别结果。这类算法虽然在某些情况下比单纯的高阶累积量识别效果要好，但是各自存在较大的局限性：
[0005]
基于幅度的k-s检验：单独对{4qam，16qam，64qam}三种qam信号识别效果较好，不适用于psk信号。这种方法对存在相位旋转的qam信号仍然有效。
[0006]
基于正交的k-s检验：仅能对没有相位旋转的{4qam/qpsk，16qam，64qam，8psk，16psk}信号进行识别。
[0007]
基于相位的k-s检验：单独对{qpsk，8psk，16psk}3种psk信号识别效果较好，不适用于qam信号。当psk信号可能有相位旋转时，可用改进的基于相位差的k-s检验进行识别。
[0008]
可见，当待识别信号的范围扩大到{4qam/qpsk，16qam，64qam，8psk，16psk}时，上述三种基于k-s检验的调制识别方法均无法做到有效识别。虽然也有文献采用折叠的方法对k-s检验进行了改进，但是没有解决上述局限，仅在原有的适用范围内提高了正确识别率。


技术实现要素：

[0009]
针对现有基于k-s检验方法不能对存在相位旋转的{qpsk/4qam，8psk，16psk，16qam，64qam}五类信号进行有效识别的问题，本发明提出一种基于高阶累积量和累积分布函数的调制识别方法，完成信号的调制识别。
[0010]
其具体技术方案如下：
[0011]
一种基于高阶累积量和累积分布函数的调制识别方法，其通过计算高阶累积量将
信号预分类为psk或qam信号，然后根据预分类结果选择k-s检验方法，完成信号的调制识别，具体包括以下的步骤：
[0012]
s1：信号预处理；
[0013]
s2：计算信号的四阶累积量c
42
，并跟预设的门限进行比较，将信号预分类为psk或qam信号；
[0014]
s3：若信号为psk信号，则采用基于相位差的k-s检验进行调制识别，识别结果为{qpsk，8psk，16psk}中的一种；
[0015]
s4：若信号为qam信号，则采用基于幅度的k-s检验进行调制识别，识别结果为{16qam，64qam}中的一种。
[0016]
进一步，步骤s1的具体过程包括：
[0017]
信号经过下变频、同步和抽取等预处理后才进行调制识别，预处理后的信号可以表示为
[0018]
r(k)＝s(k)e
jθ
+w(k)，k＝1,2,
…ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
[0019]
其中s(k)是来自标准星座图的复信号序列；θ为信道造成的未知相位，在短时间内保持不变；w(k)是复高斯白噪声序列，实部和虚部均服从均值为零，方差为σ2/2的高斯分布。
[0020]
进一步，步骤s2的具体过程包括：
[0021]
p1：首先计算高阶累积量c
42
[0022][0023]m42
＝e[r2(r
*
)2]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0024]m20
＝e[r2]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0025]m21
＝e[rr
*
]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0026]
其中上标*表示共轭；
[0027]
p2：根据五种信号的高阶累积量理论值预设识别门限；若信号识别为psk类，则执行步骤s3；若信号识别为qam类，则执行步骤s4；
[0028]
进一步，步骤s3的具体过程包括：
[0029]
若识别为psk信号，则按如下步骤进行识别：
[0030]
(a)计算复信号r(k)的相位，并对相位做差分处理，得到φ(k)，差分处理可去掉旋转相位的影响；
[0031]
(b)将φ(k)中大于π的数值对称映射到[0,π]范围，即
[0032][0033]
(c)计算φ(k)的累积分布函数fr(n)
[0034][0035]
(d)用fr(n)跟{qpsk,8psk,16psk}3种调制信号的经验相位差累积分布函数f
x
(n)分别作k-s检验，
[0036][0037]
其中x分别对应3种调制信号，最终识别结果为最小的d
x
对应的调制方式。
[0038]
进一步，若识别为qam信号，则按如下步骤进行识别
[0039]
(a)计算复信号r(k)的幅度，得到a(k)，显然a(k)跟相位旋转无关；
[0040]
(b)计算a(k)的累积分布函数fr(n)
[0041]
(c)用fr(n)跟{16qam,64qam}2种调制信号的经验幅度累积分布函数f
x
(n)分别作k-s检验，
[0042][0043]
其中x分别对应2种调制信号，最终识别结果为最小的d
x
对应的调制方式。。
[0044]
本发明所达到的有益效果为：
[0045]
相比于基于幅度的k-s检验和基于相位的k-s检验，本发明不需要预先知道信号是psk还是qam调制，放宽了k-s检验的适用范围；相比基于正交的k-s检验，本发明对经过平坦衰落信道后存在相位旋转的信号仍能有效识别。
附图说明
[0046]
图1是六种信号标准星座图；
[0047]
图2是含相位旋转和噪声的星座图；
[0048]
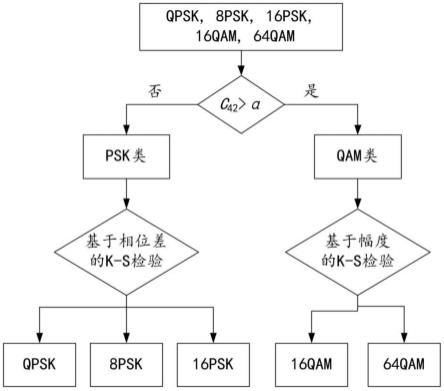
图3是五种信号的识别流程图；
[0049]
图4是psk信号基于相位差的cdf曲线；
[0050]
图5是qam信号基于幅度的cdf曲线；
[0051]
图6是五种信号的正确识别概率图。
具体实施方式
[0052]
为便于本领域的技术人员理解本发明，下面结合实施例及附图说明本发明的具体实施方式。
[0053]
本发明的技术方案是：首先通过计算高阶累积量将信号预分类为psk或qam信号，然后根据预分类结果选择合适的k-s检验方法，完成信号的调制识别。该方案主要实现步骤如下：
[0054]
接收机截获的信号经过下变频、同步和抽取等预处理后才进行调制识别，预处理后的信号可以表示为
[0055]
r(k)＝s(k)e
jθ
+w(k)，k＝1,2,
…ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(1)
[0056]
其中s(k)是来自图1所示标准星座图的复信号序列；θ为信道造成的未知相位，在短时间内保持不变；w(k)是复高斯白噪声序列，实部和虚部均服从均值为零，方差为σ2/2的高斯分布。定义信号信噪比为1/σ2，信噪比为20db时的各信号星座图如图2所示。
[0057]
本发明对五种信号的识别流程如图3所示,具体步骤如下
[0058]
(1)基于累积量区分psk和qam
[0059]
首先计算高阶累积量c
42
[0060][0061]m42
＝e[r2(r
*
)2]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0062]m20
＝e[r2]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0063]m21
＝e[rr
*
]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0064]
其中上标*表示共轭。五种信号的高阶累积量理论值如表1所示,因此取识别门限
[0065]
α＝(-1-0.68)/2＝-0.84
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)
[0066]
表1五种调制信号的c
42
理论值
[0067]
调制方式qpsk/4qam8psk16psk16qam64qamc
42
理论值-1-1-1-0.68-0.619
[0068]
若信号识别为psk类，则对其进一步计算基于相位差的累积分布函数(cdf)，然后进行k-s检验，具体过程见步骤(2)；若信号识别为qam类，则对其进一步计算基于幅度的累积分布函数，然后进行k-s检验，具体过程见步骤(3)。
[0069]
(2)基于相位的k-s检验区分psk
[0070]
若识别为psk信号，则按如下步骤进行识别
[0071]
(a)计算复信号r(k)的相位，并对相位做差分处理，得到φ(k)，差分处理可去掉旋转相位的影响；
[0072]
(b)将φ(k)中大于π的数值对称映射到[0,π]范围，即
[0073][0074]
(c)计算φ(k)的累积分布函数fr(n)
[0075][0076]
(d)用fr(n)跟{qpsk,8psk,16psk}3种调制信号的经验相位差累积分布函数f
x
(n)分别作k-s检验
[0077][0078]
其中x分别对应3种调制信号，其经验相位差cdf曲线如图4所示。最终识别结果为最小的d
x
对应的调制方式。
[0079]
(3)基于幅度的k-s检验区分qam
[0080]
若识别为qam信号，则按如下步骤进行识别
[0081]
(a)计算复信号r(k)的幅度，得到a(k)，显然a(k)跟相位旋转无关；
[0082]
(b)计算a(k)的累积分布函数fr(n)
[0083]
(c)用fr(n)跟{16qam,64qam}2种调制信号的经验幅度累积分布函数f
x
(n)分别作k-s检验
[0084][0085]
其中x分别对应2种调制信号，其经验幅度cdf曲线如图5所示。最终识别结果为最
小的d
x
对应的调制方式。
[0086]
为了验证本发明提出的基于高阶累积量和累积分布函数的调制识别方法的有效性，在matlab软件上进行了仿真。仿真条件为：对每种信号在不同信噪比下进行10000次蒙特卡洛仿真，每次的符号数量为200，每次的信号含有一个固定且未知的旋转相位，仿真中信号功率归一化，噪声功率已知。不同信噪比下的正确识别概率如图6所示，可见本发明提出的识别算法能对{qpsk/4qam，8psk，16psk，16qam，64qam}5种含有相位旋转的信号在较高信噪比时有着较好的识别效果，突破了原来单纯依靠累积分布函数进行k-s检验时在识别范围上的局限性。在信噪比snr小于11db时有些信号的识别率突然下降，是因为此时高阶累积量在预分类时出现了错误。
[0087]
以上的本发明实施方式，并不构成对本发明保护范围的限定。任何在本发明的精神和原则之内所作的修改、等同替换和改进等，均应包含在本发明的权利要求保护范围之内。