一种多频带稀疏阵列天线选择与波束形成联合设计方法

1.本发明属于稀疏阵列设计和波束形成技术，具体为一种多频带稀疏阵列天线选择与波束形成联合设计方法。


背景技术：

2.多频带天线是一种在多个频带均可有效工作的单个天线，可显著降低天线系统的体积、成本、重量和雷达散射截面，目前广泛应用于多种复杂通信与雷达系统。同时，也广泛的应用于各种现代无线电技术，如认知无线电(cognitive radio)和软件定义无线电(software defined radio)以及多输入多输出(mimo)的雷达与通信系统。随着多频带天线阵列技术的兴起和发展，一个基本的问题是如何设计最优的稀疏阵列配置方式，使得阵列在所有工作频带上均具有较好的性能。
3.目前，稀疏阵列设计研究主要集中于单频带天线。相比于均匀线性阵列，稀疏阵列在不牺牲阵列孔径和性能的同时，可显著降低系统复杂度与硬件开销。或者在满足预定设计标准的同时，通过最小化硬件和计算需求来规划天线阵元的位置，来减少接收机昂贵的链路成本。根据应用场景和性能判据，稀疏阵列设计可分为两类：环境独立型(environment-independent)阵列设计和环境依赖型阵列设计(environment-dependent)。对于环境独立型稀疏阵列设计，在doa估计中，学者们设计了多种结构化稀疏阵列，如嵌套阵列和互质阵列，这两种阵列的排布方式易于实现，具备较强的孔径扩展能力；在发射方向图合成中，学者们根据理想的发射方向图来联合设计天线位置和发射权值，可以通过交替方向乘子法(admm)等数学方法对联合优化问题进行求解。另一方面，环境依赖型稀疏阵列设计中，学者们在接收波束形成时基于最大sinr准则，根据接收数据协方差矩阵先验信息来设计天线位置和接收波束权值，以获得更好的干扰抑制性能。zhi zheng于2020年提出在最大sinr准则下，对自适应波束形成的稀疏阵列进行设计，并且引入了二次分数约束来优化波束形成器的权重，如“z.zheng,y.fu.w.-q.wang,and h.c.so,“sparse array design for adaptive beamforming via semidefinite relaxation”ieee signal process.lett.,vol.27,pp.925
–
929,2020.”中所记载。最终设计出的稀疏阵列的接收波束形成性能可与穷举法得到的最优阵列相媲美。
4.对于多频带天线阵列，syeda.hamza等学者基于群稀疏(group sparsity)重构技术研究了天线选择和接收波束形成联合设计，如“s.a.hamza and m.g.amin,“sparse array receiver beamformer design for multi-functional antenna,”in 2020 28th european signal processing conference(eusipco),2021,pp.1836
–
1840”中所述，使得阵列在不同频带下具有相同的稀疏天线位置，并联合优化各频带的接收波束权值。在最大输出sinr的前提下，引入了重加权群稀疏性，确保得到在所有频段下的通用稀疏阵列。但是，该方法没有考虑接收波束图的旁瓣抑制问题，在某些工作频率上会产生不可控的高旁瓣，从而降低了接收机对未知干扰的抑制能力。


技术实现要素：

5.本发明的目的在于提出了一种多频带稀疏阵列天线选择与波束形成联合设计方法
6.实现本发明目的的技术方案为：一种多频带稀疏阵列天线选择与波束形成联合设计方法，包括：
7.步骤1、对多频带天线阵列接收到的信号在接收端进行线性组合，构建最大输出信干噪比准则下的优化问题模型；
8.步骤2、对多频带天线数目进行稀疏选择，并且将旁瓣区域离散化，通过二次分数约束实现旁瓣电平约束；
9.步骤3、引入稀疏系数，将天线稀疏选择的约束转换到优化问题模型中，使用重加权l
1，∞
范数代替混合的l
0，2
范数实现凸松弛；
10.步骤4、采用半定松弛和重加权l
1，∞
范数逼近技术，将优化问题转化为凸子问题，迭代求解凸子问题，获得期望的权重矩阵，从权重矩阵提取出主特征向量，恢复出原始波束形成向量。
11.优选地，接收端线性组合后的信号为：
[0012][0013]
式中，表示对应的波束形成权重向量，表示接收的信号，m为窄带信号个数，表示维度为n
×
1的复数向量。
[0014]
优选地，接收的信号具体为：
[0015][0016]
式中，是入射基带信号的复振幅，和分别是在ωi频率下，角度为的期望信号和角度为的干扰信号对应的导向矢量，代表方差为的加性高斯噪声。
[0017]
优选地，最大输出信干噪比准则下的优化问题模型具体为：
[0018][0019][0020]
式中，和分别为ωi频率下期望源信号的协方差矩阵和干扰加噪声的协方差矩阵，wi为对应接收信号的波束形成权重向量，m为窄带信号个数。
[0021]
优选地，步骤2的具体方法为：
[0022]
构造一个完整的连接向量针对定义混合的l
0，2
范数：n表示第n个天线阵元位置；
[0023]
对旁瓣区域进行离散化，在每个离散化的角度下，对归一化阵列功率响应b(ωi，θ
l
)进行抑制；
[0024]
在优化问题的约束条件中，将选择出的天线数目设置为k，抑制旁瓣电平的参数设置为δ，将优化问题模型改写为：
[0025][0026][0027][0028][0029]
式中，矩阵rs和r
in
分别为ωi频率下期望源信号的协方差矩阵和干扰加噪声的协方差矩阵，wi为对应接收信号的波束形成权重向量，m为窄带信号个数，a(θ
l
，ωi)表示ωi频率下，角度θ
l
处的导向矢量。
[0030]
优选地，将旁瓣区域表示为ω，将ω离散得到一组角度样本为{θ
l
}，l＝1，
…
，l，l为角度样本个数，角度样本对应的数组流形表示为a(θ1)，...，a(θ
l
)，在θ
l
方向上的阵列功率响应具体为：
[0031][0032]
式中，θ0是期望源信号方向，w对应当前频率下的波束形成权重向量。
[0033]
优选地，步骤3的具体方法为：
[0034]
采用凸的l
1，∞
范数作为群稀疏性诱导范数来替代非凸的l
0，2
范数，其中，混合l
1，∞
范数被定义为
[0035]
引入一个重加权向量u来增强目标问题的群稀疏性，其中权重值u(1)，u(2)，...，u(n)均为正数；
[0036]
用来代替优化问题模型中的优化问题模型改写为：
[0037][0038][0039][0040]
定义将矩阵和定义如下：
[0041][0042][0043][0044]
其中，和分别表示复数变量的实部和虚部，变换后的优化问题为：
[0045][0046][0047][0048]
优选地，步骤4的具体过程为：
[0049]
将二次函数重写为：
[0050][0051]
其中，
[0052]
线性分式约束被松弛为
[0053]
使用凸的半正定规划对l
1，∞
范数的平方进行凸优化，具体为：
[0054]
定义矩阵和然后使用秩松驰的性质，l
1，∞
范数的平方被重写为：
[0055][0056]
是实数域的矩阵，推导出矩阵和满足下列约束关系：
[0057][0058]
优化问题凸松弛之后转换为：
[0059][0060][0061][0062][0063][0064][0065]
其中，u的上标r代表第r次重加权迭代，u的迭代更新公式为：
[0066][0067]
其中，ε是一个正数。
[0068]
优选地，恢复出的原始波束形成向量为：
[0069][0070]
式中，为主特征向量，in表示n
×
n维的单位矩阵，j是虚数单位。
[0071]
本发明与现有技术相比，其显著优点为：本发明在最大sinr准则与旁瓣水平约束
下，完成多频带稀疏阵列的天线选择与接收波束形成联合设计，在保证接收波束形成器具有干扰抑制能力的前提下，既可以大量节省硬件成本，又可以在所有工作频带上均显著降低波束图的旁瓣水平。
附图说明
[0072]
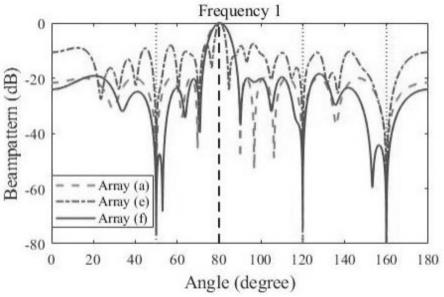
图1为ω1频率下，本发明的方法、zhi zheng的方法以及hamza的方法的波束图。
[0073]
图2为ω2频率下，本发明的方法、zhi zheng的方法以及hamza的方法的波束图。
[0074]
图3为ω3频率下，本发明的方法、zhi zheng的方法以及hamza的方法的波束图。
[0075]
图4为ω4频率下，本发明的方法、zhi zheng的方法以及hamza的方法的波束图。
[0076]
图5为三种方法分别选出的稀疏天线位置。
[0077]
图6为在ω1，ω2频率下，本发明的方法和zhi zheng的方法形成深度零陷区域的波束图。
[0078]
图7为在ω3，ω4频率下，本发明的方法和zhi zheng的方法形成深度零陷区域的波束图。
具体实施方式
[0079]
下面结合附图和实例进一步说明本发明一种多频带稀疏阵列天线选择与波束形成联合设计方法。
[0080]
一种多频带稀疏阵列天线选择与波束形成联合设计方法。需要对接收端的信号进行加权组合，基于最大化信干噪比(sinr)与旁瓣水平约束，稀疏阵列设计被描述为具有混合l
0，2
范数正则化的非凸约束优化问题。该优化问题可以保证在所有工作频带上均选择相同天线位置的同时，独立优化每个频带的波束形成权值。通过利用半定松弛和重加权l
1，∞
范数逼近技术，将该问题转化为一系列的凸子问题，然后利用已有凸优化方法求解。具体实施步骤如下：
[0081]
步骤1、假设多带天线能够处理m个以频率ωi(i＝1，
…
，m)为中心的窄带信号。考虑期望源信号工作在第i个频段，其频率为ωi，同时存在pi个干扰源。信号投射在具有n个间隔均匀的传感器阵列上，接收端的信号表示为：
[0082][0083]
其中，代表方差为的加性高斯噪声，是入射基带信号的复振幅。和分别是在ωi频率下，角度为的期望信号和角度为的干扰信号对应的导向矢量：
[0084][0085]
为了防止频谱混叠，线性阵列的阵元间距设置为ωm是多频带天线对应的最高工作频率。因此，导向矢量可以简化为：
[0086]
[0087]
接收到的信号在接收端线性组合，使得输出信干噪比(sinr)最大，表示对应的波束形成权重向量，那么波束形成器输出端的信号为：
[0088][0089]
对于多频带天线阵列接收到的信号在接收端线性组合，使得输出sinr最大。定义wi为对应接收信号的波束形成权重向量，rs和r
in
分别表示为ωi频率下期望源信号的协方差矩阵和干扰加噪声的协方差矩阵。最大输出信干噪比(maxsinr)准则下，优化问题模型为：
[0090][0091]
步骤2、对于旁瓣水平约束，首先考虑归一化阵列功率响应：
[0092][0093]
其中，θ0是期望源信号方向，即为主瓣对应的角度。在实际的应用场景中，将旁瓣区域表示为ω，再将ω离散得到一组角度样本为{θ
l
}，l＝1，
…
，l，其对应的数组流形表示为a(θ1)，...，a(θ
l
)，那么在θ
l
方向上的阵列功率响应表示为：
[0094][0095]
因为多频带天线能够接收m个频段的信号，分别对应m个波束形成权向量w1，w2，...，wm。定义向量其中wi(n)是wi的第n个分量。表示第n个天线上所有子频带权重的集合。为了避免第n根天线接收信号，向量必须被设置为0m。这意味着对于所有m个子频带，每个wi的第n项必须同时设置为0。通常情况下，稀疏阵列设计是通过从wi的n个条目中选出k个非零的元素来实现的。因此，先构造一个完整的连接向量再针对定义混合的l
0，2
范数：以此实现天线的稀疏选择。此外，在所有的频段中都添加了旁瓣电平约束，那么优化问题可以写为：
[0096][0097]
其中，矩阵
[0098]
步骤3、引入稀疏系数μ，将天线稀疏选择的约束转换到目标函数中。为了在所有频率上寻得一个共同的稀疏阵列配置，一般采用凸的l
1，∞
范数作为群稀疏性诱导范数来替代公式(8)中非凸的l
0，2
范数。其中，混合l
1，∞
范数被定义为并且再引入一个重加权向量u来增强目标问题的群稀疏性，其中权重值u(1)，u(2)，...，u(n)均为正
数。因为对凸的l
1，∞
范数取平方，并不会改变其范数的稀疏性，即用来代替目标函数中的
[0099][0100]
定义将矩阵和定义如下：
[0101][0102][0103][0104]
其中，和分别表示复数变量的实部和虚部，定义这些矩阵的目的是将优化问题中的部分矩阵和变量从复数域转化到实数域，变换后的优化问题为：
[0105][0106]
步骤4、基于maxsinr准则和旁瓣电平约束下的稀疏阵列设计是一个组合优化问题，无法在多项式的时间内求解，为了更有效地实现均匀阵列中的天线选择功能，本发明采用了凸松弛方法。由于目标函数不连续且存在二次约束，直接求解优化问题(13)非常困难。因此，采用半定松弛(sdr)和重加权l
1，∞
范数逼近技术，将上述优化问题转化为一系列的凸子问题，然后利用已有凸优化方法求解。本发明中将二次函数重写为：
[0107][0108]
其中类似的，线性分式约束被松弛为此外，使用凸的半正定规划(sdp)对l
1，∞
范数的平方进行凸优化。首先，定义还有矩阵和然后使用秩松驰的性质，l
1，∞
范数的平方可以被重写为：
[0109][0110]
是实数域的矩阵，可以推导出矩阵和满足下列约束关系：
[0111][0112]
因此，优化问题(13)被凸松弛为：
[0113][0114]
u的上标r代表第r次重加权迭代，u的迭代更新公式为：
[0115][0116]
其中，ε是一个很小的正数。
[0117]
通过迭代求解问题(17)，能够最终获得期望的权重矩阵接下来，从提取出主特征向量即：最终，恢复出原始波束形成向量：
[0118][0119]
该迭代问题求解可分为两步。第一步，求解组合优化问题，分别得到每个工作频段下波束形成权重向量；第二步，通过权重向量中选择出的天线数目，来调整μ的收缩范围，并且更新重加权矩阵ur。具体的迭代步骤为：
[0120]
1)输入参数：n＝28，k＝18，δ，ε，μ
min
，μ
max
。
[0121]
2)初始化设置：
[0122]
u是元素全为1的矩阵，其规模为n
×
n。
[0123]
3)开始迭代：
[0124]
i.通过公式(17)求得：
[0125]
ii.通过公式(19)求得：
[0126]
iii.通过公式(18)求得：u
r+1
[0127]
iv.通过二分法更新μ的值
[0128]
v.r＝r+1
[0129]
4)若即选出期望的天线数目时停止循环。
[0130]
5)输出波束形成向量：w1，w2，
…
，wm。
[0131]
实施例
[0132]
通过matlab仿真，进一步说明本发明多频带稀疏阵列天线选择与波束形成联合设计具体实施方案。
[0133]
1)仿真系统参数设置
[0134]
每次仿真从n＝28个间隔均匀线性阵列中选出k＝18个天线。多频带天线有m＝4个工作频带，分别为0.931ωm，0.944ωm，0.972ωm和ωm。其中，最大的频率ωm＝3.6ghz通常用
于5g通信系统中。设置μ＝0.1，ε＝5
×
10-4
，δ＝-20db。假定期望信号方向位于80
°
，其余三个干扰信号的角度分别为50
°
、120
°
、160
°
。期望信号的信噪比(snr)为0db，每个干扰的干噪比(inr)为40db。
[0135]
2)波束图绘制
[0136]
为了直观地显示接收端的波束形成效果，用解得的权重向量对接收信号进行加权组合，最终绘制出在不同工作频带下的波束图，并且与其它学者的研究成果进行对比。波束图的横坐标代表[0
°
，180
°
]的角度范围，对信号加权组合后的幅度值取模后进行最大值归一化，因此波束图纵坐标的单位为db。
[0137]
3)衡量指标
[0138]
在本发明中，需要衡量最终波束形成的效果，除了绘制波束图之外，还需要采用输出信干噪比(sinr)这一指标。在解得最佳的权重向量之后，代入求解公式，可以得到工作在ωi频率下的输出信干噪比：
[0139][0140]
λ
max
{
·
}表示取矩阵的主特征向量。在相同的初始条件下，输出信干噪比越大，说明波束形成的效果越好。
[0141]
4)结果分析
[0142]
本发明一共进行了两次实例仿真，图1～图4为第一次仿真实验，分别在四个频率下，绘制出三种方法的波束图，并进行效果对比。图5中的(a)～(d)分别表示四个工作频带下，zhi zheng的方法]选择出相对应的四个稀疏阵列；图5中(e)表示四个工作频带下，hamza的方法选择出的稀疏阵列；图5中(f)表示四个工作频带下，本发明的方法选择出的稀疏阵列。在某些应用场景下，波束图需要形成一个深度零陷的区域，以增强抗干扰性能。图6～图7为第二次仿真实验，我们将120
°
处的干扰替换为[115
°
，125
°
]的零陷区域，零陷深度设置为-40db，分别在四个频率下，绘制出本发明的方法与zhi zheng方法的波束图。
[0143]
通过观察比较，不难发现，三种方法均能够有效的抑制干扰信号。但是，相比于hamza方法，本发明的方法不仅能够同时工作在四个频带下，还能够产生极低的旁瓣电平，旁瓣抑制性能接近zhi zheng的方法。从表1中，可以得出，本发明的方法输出sinr性能优于hamza方法，略逊于zheng的方法。需要注意的是，zhi zheng的方法实际上是优化问题的性能上限，因为它不受每个频率下天线位置的一致性约束，因此具有更高的自由度。
[0144][0145]
表1在四种工作频率下，三种方法的输出信干噪比(db)
[0146]
通过图6和图7，可以观察出，本发明的方法和zhi zheng的方法均能够在期望的角度范围内产生更低的零陷区域。并且，在整个旁瓣区域中，本发明的方法相比于zhi zheng的方法，具有更低的旁瓣水平。
[0147]
综上，本发明所述的方法有着很好的综合性能。既能够在多个频带下进行稀疏阵
列设计和波束形成设计，还具备良好的旁瓣水平抑制和干扰抑制的性能。应用在多功能雷达与通信系统中，能够极大的节省硬件成本、降低计算复杂度，有较高的实用价值。