基于傅里叶单像素成像和双逻辑映射的多图像认证方法

本发明属于图像成像处理，具体涉及基于傅里叶单像素成像和双逻辑映射的多图像认证方法。

背景技术：

1、如今，互联网的高速发展使得越来越多的信息在网络上交互，但信息以明文形式传输时，极易遭受网络黑客的攻击，个人信息安全、国家安全面临巨大威胁。“加密-传输-解密”传输模式有效地解决了这一问题。图像作为一种典型的多媒体载体，以直观性好、携带信息量大的优点受到了人们的青睐，同时，也在网络上大量传输。因此，如何有效加密-解密图像从而保障信息的安全传输越来越受到研究人员的关注。

2、单像素成像不同于传统阵列成像，成像系统一般由光源、能够产生随机分布光强的设备(如空间光调制器(slm)、数字微镜设备(dmd)和投影仪)、透镜和一个没有空间分辨率的探测器(也称为单像素探测器或桶探测器)组成。从成像系统来看，单像素成像与传统成像最明显的区别是传统成像需要价格昂贵的以硅为光敏材料的像素化阵列探测器，如电荷耦合设备(ccd)和互补金属氧化物半导体(cmos)。跟阵列探测器相比，单像素探测器具有高灵敏度、宽光谱范围和低成本的优点。因此，在弱光、非可见光波段成像时，单像素成像技术具有巨大优势。

3、单像素成像根据光源类型可以分为随机光单像素成像(rlspi)和结构光单像素成像(slspi)。rlspi使用随机相位掩摸(rpm)调制的照明光照射成像物体，通过关联算法重构图像。为了重建高质量的图像，这种方法要求不同照明光对目标物体进行多次单像素测量，耗费了大量时间，成像效率低。为了减少测量次数，研究人员提出了压缩感知鬼成像(cgi)，该方法基于压缩感知原理，通过一个传感矩阵将稀疏域中的目标图像编码为强度值序列，使用凸优化算法重构图像。然而常见的压缩感知重构算法需要多次迭代求解最优值，需要大量时间。因此，传统的rlspi和cgi都是一种牺牲时间换质量的方法，效率较低。slspi使用结构相位掩模调制的照明光照射物体，常见的有hadamard单像素成像、傅里叶单像素成像(fsi)和离散余弦单像素成像等。结构光(如hadamard基图案、傅里叶基图案和离散余弦基图案等)由于其完备的正交性使得相同的测量次数，slspi的成像质量要明显优于rlspi，但slspi依然存在成像质量低及成像时间长的问题。

技术实现思路

1、本发明的目的是提供基于傅里叶单像素成像和双逻辑映射的多图像认证方法，解决了现有方法成像时间长以及成像质量低的问题。

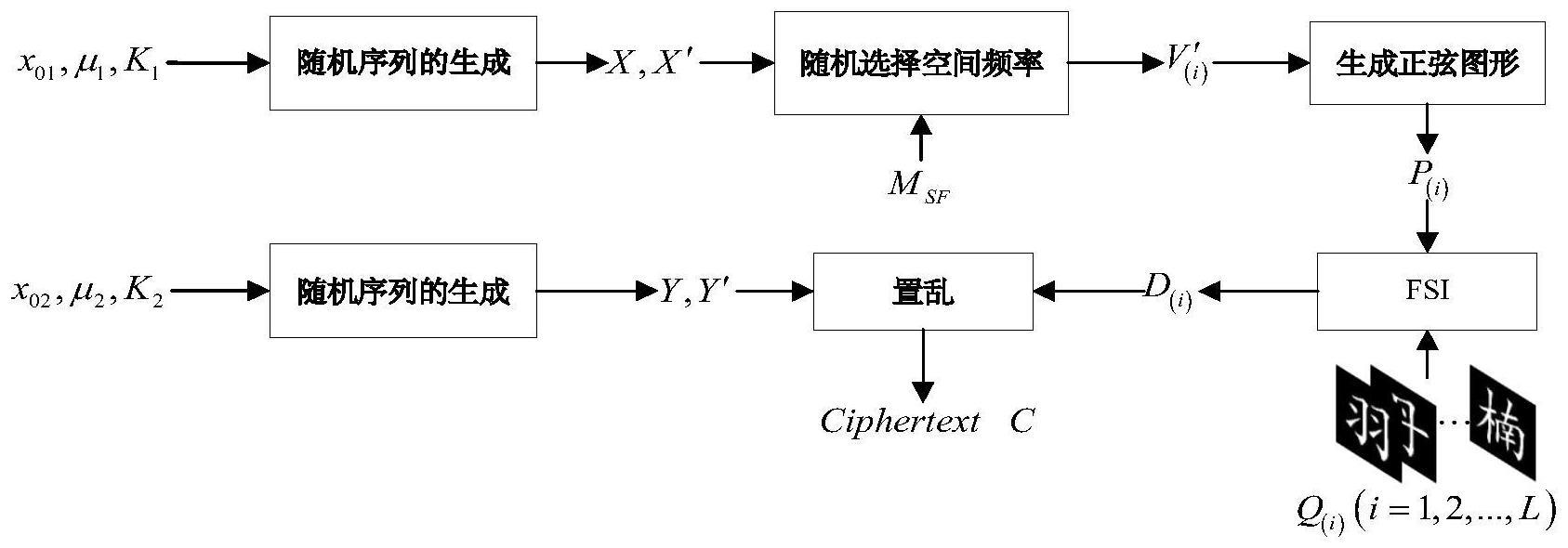
2、本发明所采用的技术方案是，基于傅里叶单像素成像和双逻辑映射的多图像认证方法，包括加密过程和解密过程；

3、加密过程的具体步骤为：

4、步骤1，使用一维逻辑映射生成随机序列x，并对随机序列x按升序排列，得到新序列x′，并将随机序列x与新序列x′进行映射，得到地址码a；

5、步骤2，选择傅里叶空间频率msf并将msf上半部分按照从左到右，从上到下顺序的排列，得到由空间频率组成的元组序列v，并根据步骤1得到的地址码a对元组序列v进行映射得到序列v′，将序列v′平均分成l组后，得到l组序列v′(i)；

6、步骤3，将步骤2得到的每组序列v′(i)通过傅里叶基图案生成公式得到灰度模式，对灰度模式使用双线性插值算法得到扩展灰度模式，再使用floyd-steinberg误差扩散抖动算法对每个扩展灰度模式进行二值化，得到二值化的傅里叶正弦模式p(i)；

7、步骤4，按照步骤2得到的每组序列v′(i)的顺序，用步骤3得到的二值化的傅里叶正弦模式p(i)对原始目标图像q(i)进行顺序照射，再用单像素检测器收集总响应d(i)；

8、步骤5，使用一维逻辑映射生成随机序列y，并对随机序列y升序排列，得到新序列y′，并将随机序列y与新序列y′进行映射，得到地址码b；

9、步骤6，将步骤4得到的所有原始目标图像q(i)的总响应值进行串联，得到一个由反射光强度组成的实值序列，将实值序列与步骤5得到的地址码b进行映射，得到密文c；

10、解密过程的具体步骤为：

11、步骤s1，使用一维逻辑映射生成随机序列y，并对随机序列y升序排列，得到新序列y′，并将随机序列y与新序列y′进行映射，得到地址码b；

12、步骤s2，根据步骤s1得到的地址码b对密文c进行逆映射，得到逆映射后的密文，将逆映射后的密文分为l组，对于原始目标图像q(i)，得到了由反射光强度组成的总响应d(i)；

13、步骤s3，将步骤s2得到的总响应d(i)进行从前向后的扫描，每提取四个值为一组，即(d0,dπ/2,d3π/2,dπ)，通过公式(7)计算提取的每组值的傅里叶频谱系数f(i)；

14、f(fx,fy)＝{d0(fx,fy)-dπ(fx,fy)+j[dπ/2(fx,fy)-d3π/2(fx,fy)]}/(2bk)  (7)

15、式(7)中，k是一个取决于探测器的大小和位置的因素，b为对比度，(fx,fy)为空间频率msf；

16、步骤s4，使用一维逻辑映射生成随机序列x，并对随机序列x′升序排列，得到新序列x′，并将随机序列x与新序列x′进行映射，得到地址码a；

17、步骤s5，将步骤s3得到的所有的傅里叶频谱系数f(i)进行串联，得到稀疏傅里叶频谱系数序列f，根据步骤s4得到的地址码a对稀疏傅里叶频谱系数序列f进行逆映射，得到逆映射后的稀疏傅里叶频谱系数序列，根据逆映射后的稀疏傅里叶频谱系数序列将傅里叶频谱系数从左到右、从上到下的顺序排列；

18、步骤s6，根据步骤s5排列的傅里叶频谱系数进行补充，得到完整的稀疏傅里叶频谱系数，对完整的稀疏傅里叶频谱系数进行二维傅里叶逆变换，得到一个包含原始目标图像信息的有噪声的重构结果；

19、步骤s7，对步骤s6得到的重构结果与原始目表图像进行非线性相关认证；

20、步骤s8，将步骤s7进行的非线性相关认证进行后处理，得到的非线性相关认证图；

21、步骤s9，根据步骤s8得到的非线性相关认证图进行认证，若认证图的中心有一个明显的尖峰或者中心强度值相对于其它位置很突出，则认证成功；若认证图为杂乱无章的状态或中心位置没有明显的尖峰，则认证失败，说明待认证图像与原始目标图像毫无关联。

22、本发明的特点还在于，

23、步骤1的具体过程为：

24、步骤1.1，给定两个一维逻辑映射的参数x0和μ1，通过公式(1)生成随机序列x＝{xi|i＝1,2,...,mn/2+k1}，并丢弃前k1个值，公式(1)如下：

25、xn+1＝μ1×xn×(1-xn)              (1)

26、式(1)中，k1为一个正整数，mn为原始目标图像q(i)的像素个数，即长有m个像素，宽有n个像素；

27、步骤1.2，将步骤1.1得到的随机序列x按升序排列，得到新序列x′，将随机序列x与新序列x′进行映射，得到地址码a。

28、步骤3的具体过程为：

29、步骤3.1，将步骤2得到的每组序列v′(i)通过傅里叶基图案生成公式得到像素为m×n的灰度模式，则傅里叶基图案生成公式如下；

30、pφ(x,y；fx,fy)＝a+b·cos(2πfxx+2πfyy+φ)    (2)

31、式(2)中，(x,y)表示图案的空域坐标；a为直流项，等于图案的平均强度值；b为对比度，(fx,fy)为空间频率msf，φ为相位；

32、步骤3.2，使用双线性插值算法对步骤3.1得到的每组灰度模式进行d倍上采样，构造一个具有像素为w×h的扩展灰度模式，扩展灰度模式与原始目标图像q(i)大小相同；

33、步骤3.3，使用floyd-steinberg误差扩散抖动算法对步骤3.2得到的每个扩展灰度模式进行二值化，得到二值化的傅里叶正弦模式p(i)；

34、使用floyd-steinberg误差扩散抖动算法进行二值化的表达式为：

35、

36、式(3)中，*标记的像素是当前被扫描的像素，空白像素是之前被扫描的像素，在从左到右、从上到下扫描一个扩展灰度模式后，其平均量化误差将接近于零。

37、步骤4的具体过程为：

38、步骤4.1，按照步骤2得到的每组序列v′(i)的顺序，用步骤3得到的二值化的傅里叶正弦模式p(i)对原始目标图像q(i)进行顺序照射；

39、步骤4.2，按照步骤4.1的操作，使用公式(4)和公式(5)，由单像素检测器收集总响应d(i)；

40、dφ(fx,fy)＝dn+keφ(fx,fy)           (4)

41、

42、式(4)和式(5)中，dn表示环境光照明的响应，k是一个取决于探测器的大小和位置的因素，ω为照明场景，q(x,y)为对象图像的表面反射率分布函数。

43、步骤5的具体过程为：

44、步骤5.1，给定两个一维逻辑映射的参数y0和μ2，通过公式(6)生成随机序列y＝{yi|i＝1,2,...,mn/2+k2}，并丢弃前k2个值，公式(6)如下：

45、yn+1＝μ2×yn×(1-yn)                 (6)

46、步骤5.2，将步骤5.1得到的随机序列y按升序排列，得到新序列y′，将随机序列y与新序列y′进行映射，得到地址码b。

47、步骤s1的具体过程为：

48、步骤s1.1，给定两个一维逻辑映射的参数y0和μ2，通过公式(6)生成随机序列y＝{yi|i＝1,2,...,mn/2+k2}，并丢弃前k2个值；

49、步骤s1.2，将步骤s1.1得到的随机序列y按升序排列，得到新序列y′，将随机序列y与新序列y′进行映射，得到地址码b。

50、步骤4的具体过程为：

51、步骤s4.1，给定两个一维逻辑映射的参数x0和μ1，通过公式(1)生成随机序列x＝{xi|i＝1,2,...,mn/2+k1}，并丢弃前k1个值；

52、步骤s4.2，将步骤s4.1得到的随机序列x按升序排列，得到新序列x′，将随机序列x与新序列x′进行映射，得到地址码a。

53、步骤6的具体过程为：

54、步骤s6.1，保留步骤s5排列的傅里叶频谱系数的上半部分，下半部分系数设置为0；

55、步骤s6.2，根据步骤s6.1保留的傅里叶频谱系数上半部分通过傅里叶频谱系数的共轭对称性将步骤s6.1傅里叶频谱系数的下半部分补齐，得到完整的稀疏傅里叶频谱系数；

56、步骤s6.3，将步骤s6.2得到的稀疏傅里叶频谱系数，对其进行傅里叶逆变换，得到一个包含原始目标图像信息的有噪声的重构结果，重构结果的像素大小为m×n；

57、傅里叶逆变换的表达式为：

58、o(x,y)＝f-1{f(μ,ν)}           (8)

59、式(8)中，f-1{·}表示二维傅里叶逆变换，(μ,ν)为傅里叶域坐标。

60、步骤s7的具体过程为：

61、步骤s7.1，根据步骤s6得到的重构结果，对像素为w×h的原始目标图像进行d倍降采样；

62、步骤s7.2，将步骤s7.1得到的降采样的原始目标图像与原始目标图像进行非线性相关认证，表达式为：

63、

64、式(9)中，为降采样的原始目标图像，q′(i)为重构结果。

65、步骤s8中后处理的表达式为：

66、nc(nc＜((max(nc)-min(nc))*0.6)+min(nc))＝0  (10)

67、

68、式(10)和式(11)中，max(·)和min(·)分别表示最大函数和最小函数，为增强系数。

69、本发明的有益效果是：

70、(1)本发明方法基于较小尺寸的空间频率分布对待验证的目标图像进行随机采样，并使用floyd-steinberg误差扩散抖动算法将每个频率生成的傅里叶正弦模式转换为二值化照明模式，在密文生成过程中，使用两个混沌序列随机选择每个对象图像的空间频率，并对所有测量值进行打乱，大大提高测量效率；

71、(2)本发明方法将逻辑映射的初始值、分岔参数以及丢弃值作为密钥，可以大大提高密码系统的安全性。