一种针对网络物理系统的网络攻击弹性约束跟踪控制方法与流程

本发明涉及网络安全技术，具体为一种针对网络物理系统的网络攻击弹性约束跟踪控制方法。

背景技术：

1、网络物理系统(cps)是一种机制，这种机制是基于计算机算法的控制或监控，整个系统与网络整合在一起，网络物理系统通常被称为大规模、地理分散、复杂和异构的物联网。近年来，各种类型的网络物理系统的发展和部署呈指数式增长，给日常生活的方方面面都带来了巨大的影响，例如，在电网、运输系统、医疗保健设备和家用电器等方面。许多这样的系统被部署在关键的基础设施、生命支持设备，或者对我们日常生活极其重要的地方。

2、在物联网中跨网络部署的cps应用程序的多样性，使其容易受到不同级别系统之间的网络攻击和物理攻击，特别是在智能制造过程中的消息传输方面。这样便在cps应用程序引入了安全隐患，导致程序变得失控，并且伤害到依赖该程序的人。

技术实现思路

1、本发明的目的在于提供一种针对网络物理系统的网络攻击弹性约束跟踪控制方法，以解决背景技术中提出的问题。

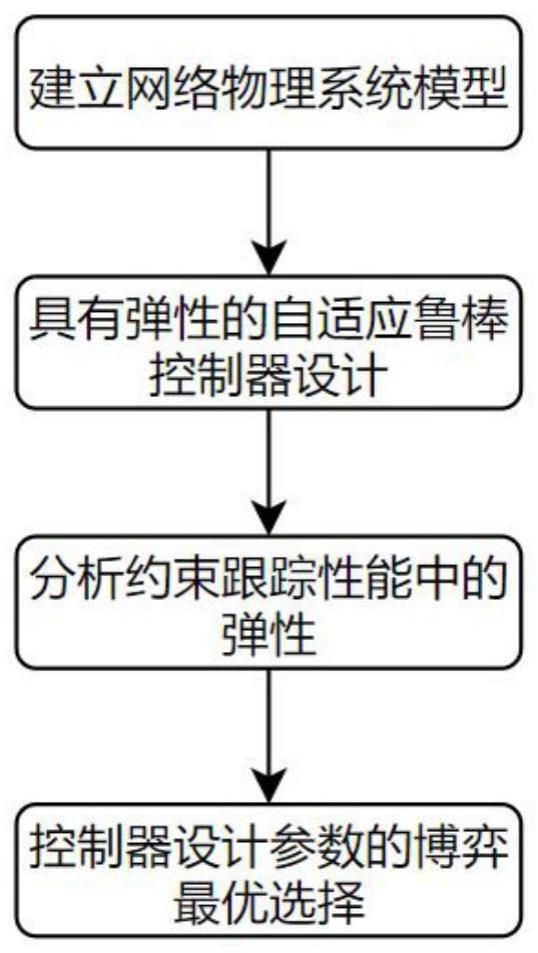
2、为实现上述目的，本发明提供如下技术方案：一种针对网络物理系统的网络攻击弹性约束跟踪控制方法，步骤1：建立网络物理系统模型，考虑网络物理系统受到一组优先级未知的网络攻击：

3、

4、式中：t∈r是时间，q(t)∈rn是坐标，是速度，是加速度，是不确定参数，是未知的网络攻击输入，δ(t)∈r是由于欺骗和/或混合威胁攻击造成的不确定攻击因子，τ(t)∈rn是控制输入。集合∑和υa是紧凑的，分别代表σ和va可能所属的区域。此外，m(q，σ，t)是惯性矩阵，是科里奥利/离心力，g(q，σ，t)是引力，是网络攻击输入矩阵。矩阵/向量m(q，σ，t)，，g(q，σ，t)和具有适当的维数。函数m(·)，c(·)，g(·)，ba(·)是连续的；

5、提出了以下约束条件。

6、

7、其中是的第i个成分，ali(·)和cl(·)都是c1，m≤n。它们是约束条件的一阶形式。每个约束可能是完整的或非完整的。约束条件可以用矩阵形式表示

8、

9、其中a＝[ali]m×n，c＝[c1 c2 … cm]t

10、步骤2：设计具有弹性约束的自适应鲁棒控制器：

11、

12、式中：表示约束跟随误差以0表示m的“标称”部分，函数是连续的，p∈rm×m，p＞0，κ＞0是一个标量设计参数；

13、

14、式中：是一个标量设计参数，是一个已知函数；

15、具有弹性约束的自适应鲁棒控制器为：

16、

17、考虑网络物理系统，控制器使系统具有以下性能：

18、(101)一致有界性：对于任意r＞0，存在一个d(r)＜∞，使得如果那么对于所有t≥t0，

19、(102)一致的最终有界性：对于任何r＞0且存在一个d＞0，使得对于任何当其中

20、步骤3：分析约束跟踪性能中的弹性：

21、当t≥t0时，均匀有界性保证了误差β后的约束被限制在区域d(r)内。统一的最终有界性性能保证了误差β足够小，即在有限时间之后在的区域内。d(r)和都与r相关。对于所有σ∈∑，va∈υa，如果存在一个区域q使则被控系统对攻击因子δ和网络攻击输入具有弹性；

22、步骤4：控制器设计参数的博弈最优选择：

23、提出了一个非合作博弈和两个stackelberg竞争的三种博弈规则来选择最优控制涉及参数；

24、进一步的，在步骤1中所提到的约束条件有两种解释方法，首先，约束可能是被动的，也就是说环境或结构是为了使系统服从约束而提供约束力的；第二，约束可能很活跃，也就是说系统的控制输入提供所需的力，以满足约束；

25、进一步的，采用第二种约束方法，并将约束对t求导：

26、

27、进一步的，约束条件的二阶形式可以改写为：

28、

29、其中l＝1，…，m；

30、

31、其中b＝[b1 b2 … bm]t；

32、进一步的，在步骤2中建立具有弹性约束的自适应鲁棒控制器之前，首先需要进行不确定性分解和网络攻击输入矩阵分解；

33、进一步的对不确定性分解进行解释，我们首先提出以下假设；

34、假设1.对于每个(q，t)∈rn×r，σ∈∑，m(q，σ，t)＞0，这个假设在大多数应用中都是有效的；我们现在在设计控制τ时考虑到不确定性。让以表示“标称”部分，函数是连续的。

35、令

36、于是我们可以得到

37、δd(q，σ，t)＝d(q，t)e(q，σ，t)

38、假设2：对于每个(q，t)∈rn×r，a(q，t)是满秩的。这意味着a(q，t)at(q，t)是可逆的。

39、假设3：在假设2的基础下，对于给定的p∈rm×m，p＞0，令

40、

41、存在一个常数ρe＞-1，它可能是未知的，使得对于所有(q，t)∈rn×r，

42、

43、这里λm(·)是矩阵的特征值。

44、由于不确定界∑是未知的，常数ρe是未知的。当没有不确定性时，e＝0，w＝0，因此可以选择ρe＝0。因此，通过连续性，该假设将不确定性的影响强加到m与之间的可能偏差的某个阈值内，这是单向的。

45、进一步的对网络攻击输入矩阵分解进行解释，我们提出对网络攻击输入矩阵ba的分解，网络攻击通过ba来影响cps。在假设2保证(ad)(ad)t可逆的前提下，令

46、

47、这里

48、

49、

50、定理1：根据假设2，那么对于任何不确定度v

51、

52、证明：我们有

53、

54、这意味着网络攻击输入v通过输入矩阵将不会对系统性能产生影响

55、进一步的，对于具有不确定性和网络攻击输入的信息物理系统，可以提出一种弹性鲁棒控制方法，首先呈现以下内容；

56、假设4：存在已知或未知的δ＞0，使得对于所有t∈r，δ≤δ(t)≤1；

57、假设5：存在一个已知或未知的常数向量和一个已知函数使得对于所有σ∈∑，va∈υa，

58、

59、这里函数π(·)可以解释为不确定界限的结构。常数向量α可能与边界集∑和υa有关；

60、让表示约束跟随误差在假设3的限制条件下，让

61、

62、其中κ＞0是一个标量设计参数。在假设5的限制条件下，让让

63、

64、是一个标量设计参数。

65、现在提出控制

66、

67、这里考虑了近似约束跟随问题。也就是说，β≠0(因此)。这可能是由于建模的不确定性。此外，系统在开始时可能不以约束流形开始(即β≠0，当t＝t0)；

68、令

69、考虑系统(1)，在假设1-5的前提下，控制(12)使系统具有以下性能：

70、(1)一致有界性：对于任意r＞0，存在一个d(r)＜∞，使得如果那么对于所有t≥t0，

71、(2)一致的最终有界性：对于任何r＞0且存在一个d＞0，使得对于任何当其中

72、进一步的对一直有界性和一直最终有界性进行证明：

73、令v＝βtpβ.(13)

74、首先，通过式(13)可以得到

75、

76、通过分解m-1＝d+δd和我们有。

77、

78、由式(8)，通过式(9)和

79、

80、基于式(10)

81、

82、

83、通过并执行矩阵对消，我们有

84、

85、通过δd＝de，采用rayleigh原理，我们有

86、

87、通过δd＝de，

88、

89、通过类似于p1的代数运算，我们可以证明

90、

91、另外

92、

93、合并式(21)和式(22)，

94、

95、因此，利用式(16)，式(19)和式(23)，我们有

96、

97、如果

98、

99、如果

100、

101、因此我们可以得出一个结论，对于所有的

102、

103、其中在调用标准参数后，

104、

105、

106、其中γ1＝λmin(p)，γ2＝λmax(p)，此外，对于任意一致最终有界性也服从于

107、

108、

109、进一步的，在步骤3中分析约束跟踪性能的弹性分为两种情况，第一为没有dos(拒绝服务)攻击和网络攻击输入，第二为dos和网络攻击输入都存在；

110、进一步的，如果没有dos(拒绝服务)攻击，则δ(t)≡1。如果没有网络攻击输入，则va(t)≡0。在这种特殊情况下，我们减少了的值，因为它只需要考虑σ的界，而不需要考虑va的界，后者反过来又减少了η的值(下面表示为ηreduced)。那么r简化为

111、

112、r的减小反过来又会使d(r)(对于r＞r)和d减小。即一致有界区域和一致最终有界区域都将减小，这意味着约束在性能之后的增强。另外，如果ηreduced和ρe都已知，则可以通过选择合适的κ来选择合适的rreduced，这是一个对照设计参数；

113、进一步的，当网络物理系统受到dos攻击和其他网络攻击时，得到的r如(29)所示，其中δ≤1，需要解释攻击影响。这意味着与没有dos和网络攻击输入时相比，性能约束的恶化，因为(29)中的r大于rreduced；另一方面，值得注意的是(29)中的r始终存在于任意δ＞0和任意有限(这与σ和va的界有关)；这意味着被控制的cps对dos攻击和网络攻击输入具有弹性；

114、进一步的，在步骤4中非合作博弈是一种零和博弈，stackelberg是一种战略博弈；

115、进一步的，利用非合作博弈进行最优控制参数选择，假设有两个参与人1和2参与人1是κ，参与人2是δ，参与人1代表系统的利益，参与人2代表网络攻击者的利益；令

116、

117、第一项由(29)中的r通过用δ替换δ得到，与一致有界和一致最终有界区域的大小有关。第二项与控制成本有关，ω＞0是一个权重因子，

118、参与人1的成本是

119、j1(κ，δ)＝j(κ，δ)  (34)

120、参与人2的成本是

121、j2(κ，δ)＝-j(κ，δ).(35)

122、每个参与者都打算做出自己的决定，使自己的成本最小化；

123、显然j1(κ，δ)+j2(κ，δ)＝0，这意味着这是一个两人零和博弈。

124、定义2：将参与人1和2的允许决策区域分别表示为d1＝(0，∞)和d2＝[δ，1]；

125、考虑一个决策偶(κ*，δ*)∈d1×d2。对于所有的κ∈d1和δ∈d2，

126、j1(κ*，δ*)≤j1(κ，δ*)，j2(κ*，δ*)≤j2(κ*，δ)  (36)

127、定义3：决策偶(κ*，δ*)∈d1×d2是一个鞍点，如果对于所有的κ∈d1，且δ∈d2，

128、j(κ*，δ)≤j(κ*，δ*)≤j(κ，δ*)  (37)

129、引理1：考虑两人零和游戏。鞍点总是纳什均衡，反之亦然；

130、证明：

131、假设(κ*，δ*)∈d1×d2是一个鞍点：

132、j(κ*，δ)≤j(κ*，δ*)≤j(κ，δ*)  (38)

133、由于j＝j1，因此：

134、j(κ*，δ*)≤j(κ，δ*)or j1(κ*，δ*)≤j1(κ，δ*).

135、由于j＝-j2，又可以得到

136、j(κ*，δ)≤j(κ*，δ*)or-j2(κ*，δ)≤-j2(κ*，δ*).

137、后者的结果是，去掉负号，反转不等号，

138、j2(κ*，δ)≥j2(κ*，δ*)

139、因此，鞍点总是纳什均衡；反过来也可以得到同样的证明；

140、这一引理表明，纳什均衡可以通过分析单个成本j(通过寻找其最小值和最大值)来求解，而不是分别分析j1和j2。

141、现在我们来解纳什均衡，我们利用引理1单独分析j；求导，我们有

142、

143、

144、其中

145、

146、因此

147、

148、对于所有的κ∈d1，δ∈d2，因此，通过式(42)，

149、δ*＝δ.(43)

150、通过可以得到

151、

152、意味着：

153、

154、由于δ＝δ，我们解的κ*：

155、

156、我们注意到当κ＝κ*，δ＝δ*时

157、

158、因此，(κ*，δ*)确实是纳什均衡。

159、进一步的，利用stackelberg竞争来选择最优控制参数，

160、“最优”的解决方案是基于游戏的“规则”。

161、在一款游戏中的“最佳”并不意味着在另一款游戏中也是最佳的。因此，为了进行比较，我们考虑另一种博弈：stackelberg竞争。

162、stackelberg竞争是一种战略博弈，领导者先行动，然后跟随者依次行动。领导者必须事先知道追随者观察了他的行为。通过了解领导者的行为，追随者会对相应的理性行为做出反应。

163、我们考虑领导者和追随者的两种可能选择

164、(1)参与人1是领导者，参与人2是追随者：对于参与人1的任何给定动作κ，追随者(参与人2)决定选择相应的动作δ来最小化j2(或最大化j)。也就是说，基于(33)，对于给定的κ，参与人2总是会做出选择

165、δ＝δ.(47)

166、知道这是参与人2会做的，参与人1为了最小化，选择了κ

167、

168、这意味着，通过与(39)-(46)相同的分析，

169、

170、stackelberg策略(47)和(49)与纳什均衡(43)和(46)相同。

171、(2)参与人2是领导者，参与人1是追随者：对于参与人2(领导者)的任何给定行动δ，参与人1(追随者)决定选择相应的行动κ来最小化j1。也就是说，根据(33)对于给定的δ，参与人1总是选择κ来最小化

172、

173、这意味着通过可解的κ

174、

175、知道这是参与人1的做法，参与人2选择δ来最小化j(κ，δ)，这意味着δ＝δ

176、根据这个选择，参与人1选择，通过解的κ

177、

178、此stackelberg策略(52)和(53)与前面的(47)和(49)相同，也与纳什均衡(43)和(46)相同；

179、博弈论框架要求，在分析了三条博弈规则(即一条非合作博弈规则和两条stackelberg竞争规则)后，控制设计参数κ存在唯一的“最优”选择。

180、与现有技术相比，本发明的有益效果是：

181、1、本发明针对具有不确定性和可能被网络攻击的网络物理系统，通过一个创造性的控制器设计，验证被控系统对网络攻击输入和其他欺骗或混合威胁攻击的弹性；提出了一个非合作博弈和两个stackelberg竞争的三种博弈规则来选择最优控制涉及参数，并证明最优选择在这三种规则中是唯一的。采用本发明方法可以使网络物理系统具有抵御网络攻击输入和其他欺骗或混合威胁攻击的能力。