具有模态耦合环形膜片的声学压缩腔室的制作方法

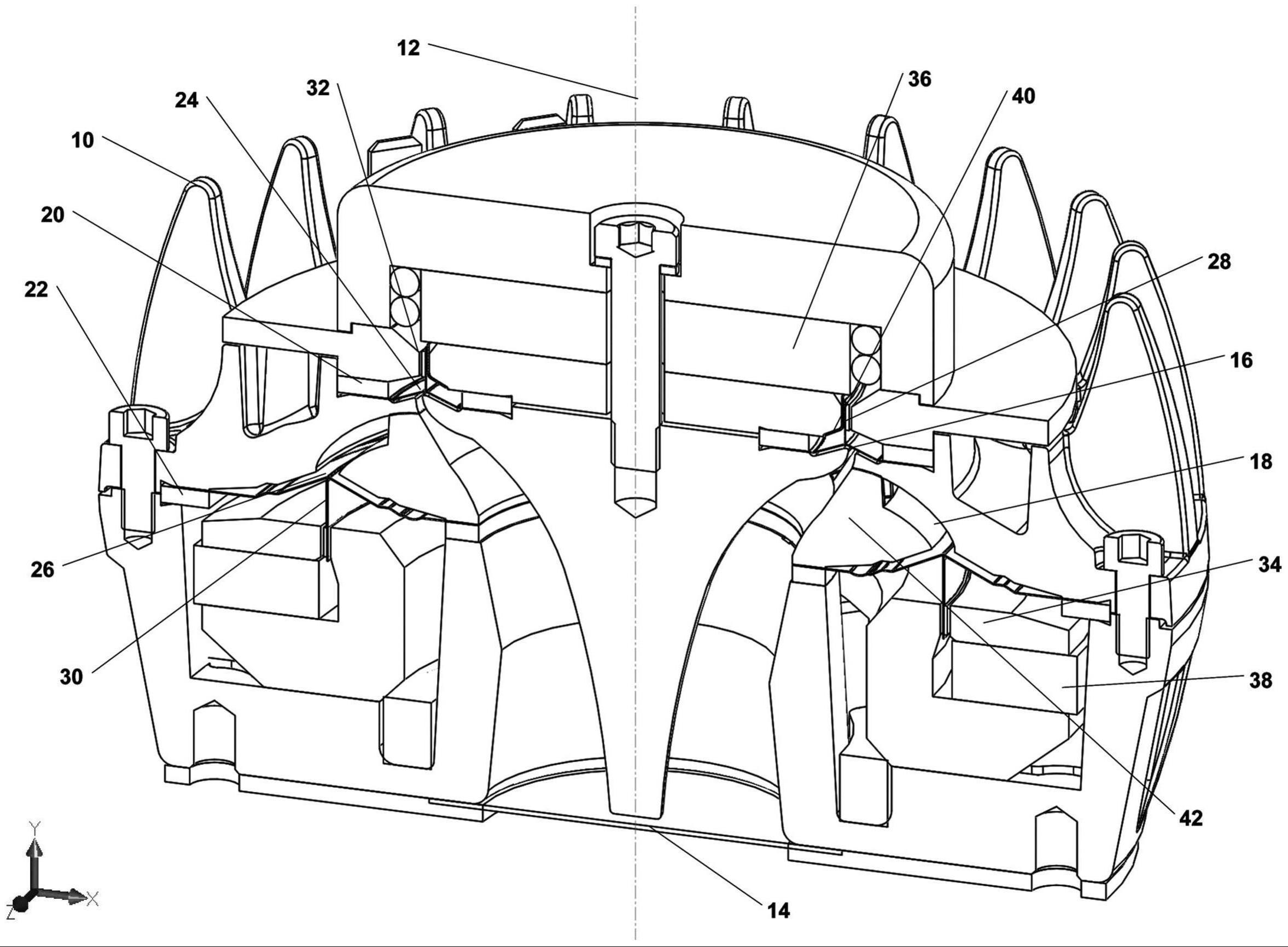
实施方式涉及电动压缩驱动器，该驱动器包括部分地以(一个或多个)环形膜片为边界的(bounded，限制的)(一个或多个)压缩腔室(compression chamber)，其中膜片的机械模式已被分析为声学耦合到压缩腔室至总体出口辐射。

背景技术：

1、自从机械音频回放出现以来，声音再现一直受到空气相对于声学膜片材料的各种不同机械性质的约束。1929年，thuras的专利“electrodynamic device(电动装置)”(us1707544a)出现了处理这些挑战的持久方法。在此，“硬盘形的”振动膜片在它的周边处被夹紧在“声音腔室”内。然后膜片由“金属塞”封闭，这允许声学振动在膜片的总表面积的受约束部分上朝向出口转移。然后声音通过通常被称为喇叭、波导或声学变压器的扩展通道离开这个组件(us4325456a)。

2、thuras专利的结构的目的是使邻近膜片的空气团更紧密地匹配膜片的相对低的顺应部(compliance)，然后逐渐转变为匹配自由空间的较高的顺应部。通俗地说，这种类型的电动转换器(transducer，换能器)被称为“压缩驱动器”；金属塞通常被称为“相位塞”；包括相位塞的出口与膜片之间的体积被称为“压缩腔室”。

3、在过去的几十年里，已对这种基本结构做出了许多改进。为了追求更多的声音输出、更低的频率扩展，或两者兼而有之，压缩驱动器的尺寸也在增加。由于音频再现涉及的波长范围较广，较大的膜片、声音腔室等产生的声学结构更有可能在频率再现带宽内具有模态共振。一旦电动转换器内的任何机械结构的尺寸具有与声音波长相比拟的尺寸，就有可能出现模态行为。

4、为了超越thuras专利的圆顶振动膜片结构，早在1932年就公开了使用环形膜片的压缩驱动器，参见us1845768。环形膜片具有优于圆顶膜片的优势，因为辐射膜片表面的局部几何形状相对于波长来说可具有比较小的径向尺寸，同时允许大的总辐射面积和强的电动驱动组件。

5、无论是圆顶还是环形，传统观点都是为了避免振动膜、相关的压缩腔室和总体压缩驱动器组件内的机械和/或声学共振。各种优化措施都试图减少、避免或以其他方式防止附加膜片和/或压缩腔室共振与声学输出的耦合。在不能避免附加模式的情况下，努力将模态频率移出声学再现装置的频率范围之外。

6、减小机械尺寸提高了膜片模态行为和/或压缩腔室的频率。增加膜片的刚度也会增加组件中开始更高阶模式的频率。这些模态避免方法都是确立已久的。对于试图减少、避免或以其他方式防止模态行为的耦合的压缩驱动器的示例，参见us8121330b2(用于圆顶膜片)和us8280091b2(用于环形膜片)。us8280091b2还公开了通过将总膜片辐射面积分成两个单独的、较小的环形膜来减少环形膜片几何形状的最大尺寸，这两个环形膜互相反平行地振荡，具有通往环形膜片的内部的共同出口导管。多个更小的膜片和压缩腔室减小了物理尺寸，其目的是将共振移到更高的频率，理想地，移出到出口辐射的频率范围之外。

7、如果出口辐射的频率足够高，最终都会发生所有组件的模态行为。对避免模式的历史性关注是工程权衡的结果。如果将子组件的尺寸约束在待产生的最大频率的波长以下，那么通常不会建立附加模式。没有必要进行附加计算来从这个规则(rubric)中获得积极的结果。

8、然而，并非所有过去的公开都是为了避免模态行为。例如，us10531200b2考虑借助于具有不同膜片厚度和边缘夹紧的两个不同环形膜片在压缩驱动器内产生两个不同的基本机械共振。us10327068b2提出了环形膜片中的附加机械共振，以增加声压。这些专利都提到了通过数值方法(numerical method，计算方法)进行模拟，以帮助实现成功的实施方式。

9、即使随着计算能力的提高，以及用于模拟耦合机械-声学系统的数值方法的普遍的工具可用性，压缩驱动器的设计仍然保持挑战性。对机械、声学和流体行为的全模拟导致了缓慢的模拟(例如，若干天与若干分钟相比)。此外，工程材料的基础模型并不总是反映物理上实现的驱动器的声学响应。因此，期望减少模拟的复杂性，以促进压缩驱动器设计的更快速迭代。

技术实现思路

1、我们提出了一种压缩腔室，其中腔室的相关环形振动膜片的机械模式被控制，并且以支持压缩驱动器的总体声学输出的方式耦合到压缩腔室。膜片的机械振动模式必须考虑频率、振幅、相位以及从压缩腔体(compression cavity，压缩腔室)到总体出口辐射的声学耦合。

2、优化整个组合的机械-声学系统是非凡的。膜片机械模式、腔室声学模式、流体行为以及它们的各种交叉作用导致了用于模拟和优化的巨大参数空间。我们通过公开用于分析与声学出口辐射的模态耦合的有效方法，来克服行业的局限性。为了促进更快的设计，我们限定了以下方法：

3、1.约束压缩腔室设计。

4、2.限定用于计算声学耦合的集总(lumped，集中)参数模型。

5、3.在没有流体影响的情况下，计算膜片模式。

6、4.仅分析零赫兹声学耦合模式。

7、由于设计过程不考虑更高阶的压缩腔室声学模式，我们从没有这些模式的预限定压缩腔室开始。该腔室具有的尺寸选择为主要支持零赫兹、或零声学模式。这个条件对于环形压缩腔室来说是很容易实现的，因为即使具有大的音圈半径，腔室的径向尺寸也较小。接下来，将压缩腔室的几何形状约束为环形设计，以允许进行下面讨论的声学耦合分析。虽然不是计算的必要条件，但使得压缩腔室为轴对称的这个最终要求支持我们加快分析的目的。

8、我们的设计周期的开展如下：

9、1)从一组件开始，该组件包括与具有单一出口导管的环形的、轴对称的压缩腔室腔体耦合的环形膜片。

10、然后压缩腔室的零赫兹声学模式或零模式代表在腔室内没有任何高阶声学波组分的声学行为：

11、2)通过具有带通滤波器的一般形式的集总参数模型来限定用于压缩腔室和膜片的零模式的声学耦合行为。

12、接下来考虑环形膜片的机械行为：

13、3)执行环形膜片的本征模式(eigenmode)模拟，忽略空气对膜片的影响，即，膜片就像在真空中一样。

14、膜片的本征模式模拟是使用有限元分析(fea)或其他数值方法实现的。免除关于邻近振动膜片的流体行为的计算简化和加快了计算。如果它们存在，封闭形式的方法也可以用于膜片中的模态计算。

15、下一个需求是分析在压缩腔室出口处声学辐射响应与膜片的机械模式之间的耦合的方法。为了开发这个方法，首先我们考虑1953年b.smith关于抑制带有扁平刚性膜片的压缩腔室中的声学腔体模式的工作。(参见b.h.smith的“an investigation of the airchamber of horn type loudspeakers(喇叭式扬声器的空气腔室的调查)”，j acoust socam，第25卷，第2期，第305-312页，1953年3月)。smith的工作试图将理想化(无模式)的膜片与高阶压缩腔室声学模式的机械耦合最小化。smith的工作后来被j.oclee-brown扩展到考虑具有非刚性膜片的模态耦合。(参见j.oclee-brown，“wideband compression-driverdesign.part 1:a theoretical approach to designing compression drivers withnon-rigid diaphragms(宽带压缩-驱动器设计。第1部分：设计具有非刚性膜片的压缩驱动器的理论方法)”，发表于2015年的第139届音频工程协会大会)。非刚性膜片表现出可能与压缩腔室声学地耦合的本征模式。

16、虽然oclee-brown的形式体系寻求使得膜片(k)与声学模式(n)之间的较高模态耦合因数(γnk)最小化，但他的工作包括有用的方法，该方法替代考虑机械模式的有意耦合。oclee-brown的工作被用来限定压缩腔室的声学出口辐射与膜片本征模式之间的一般路径：

17、4)使用oclee-brown，计算环形膜片本征模式3)和仅考虑由2)表示的零声学模式的压缩腔室之间的“受迫的模态耦合”水平。

18、压缩腔体的每一个较高的膜片机械模式(k>1)的耦合与具有零声学模式(n＝0)的基本模式(k＝1)的耦合进行比较。oclee-brown的形式体系还考虑了n>0，但(2)的集总参数模型没有考虑压缩腔室的较高阶声学模式。

19、1)-4)提供了压缩腔室的基线声学响应和初始环形膜片几何形状。在膜片本征模式与压缩腔体之间的耦合被量化的情况下，下一步是修改环形膜片的几何形状：

20、修改环形膜片几何形状的方式是控制、添加、转移、去除或以其他方式操纵它的本征模式。通过重复3)和4)的分析，观察对总体声学响应的影响。

21、以迭代的方式执行1)-5)的序列，其中膜片几何形状被反复修改，且所得到的计算结果被用来分析总体声学响应。膜片的总体尺寸和几何截面被参数化，以促进每个新的出口辐射耦合的迭代修改和计算。

22、相对于完整的机械-声学模拟来说所得到的计算是简化的，并提供了与物理实施例的测量行为的相关性。该简化的计算能够具有更短的迭代和缩短的设计周期。更快速的计算以有利于压缩驱动器的总体声学出口辐射的方式解锁了限定、分析、测试和最终使用膜片机械模式的可能性。