一种单通道时频混叠信号符号时延与频偏联合盲估计方法

本发明涉及通信信息传输领域， 尤其涉及一种单通道时频混叠信号符号时延与频偏联合盲估计方法。

背景技术：

1、随着现代卫星通信技术的快速发展，卫星通信在应急救援、 自动驾驶以及智能网联等场景的应用愈发广泛，面临的通信安全问题与频谱资源紧缺问题也变得愈发严峻[1]，卫星运营商也对卫星通信系统的安全性与频带利用率提出了更高要求。为解决此类问题，美国viasat公司的markdankberg于1998年提出了一种名为成对载波多址接入(pairedcarrier multiple access,pcma)的通信技术[2]，该技术使得通信双方可同时利用相同频带资源进行信息传输，具有较强的抗截获能力以及理论上相较于传统通信体制高一倍的频带利用率。pcma技术所具备的高安全性与强负载能力也使得其近年来被逐渐应用于多种新一代卫星通信网络中，作为通信第三方如何对其进行有效监管也逐渐成为一大研究热点。本发明中将pcma技术对应通信信号统称为时频混叠信号。

2、时频混叠信号处理主要可分为检测识别[3]、参数估计[4]以及分离[5]等三个阶段，符号时延与频偏作为分离阶段不可或缺的两个重要参数，通常需在参数估计阶段进行重点估计。常见时频混叠信号符号时延与频偏估计算法可分为数据辅助估计算法和盲估计算法两类，数据辅助估计算法性能较好但需预知辅助序列，而盲估计算法虽然性能一般但无需预知辅助序列因此应用场景更为广泛。在数据辅助估计算法方面，瞿孟虹等[6]利用最大似然递推估计完成了频偏、相偏以及信道参数的联合估计，但复杂度相对较高。yang等[7]利用同步序列与最大似然估计完成了频偏估计，但仅适用于8psk信号。魏雪娟等[8]利用二维步进搜索完成了符号时延和频偏的联合估计，复杂度较低，但算法性能受门限设定值影响较大。b.song等[9]利用最大似然特征完成了频偏估计，但未考虑子载波频偏存在差异的情况。f.li等[10]利用帧循环特征完成了符号时延和频偏的联合估计，但仅可处理特定帧格式信号。而在盲估计算法方面，曲阜平等[11]利用信赖域完成了符号时延估计，但算法结构复杂且主要针对qpsk信号。付君等[12]利用比特软信息完成了符号时延、频偏以及幅度的联合估计，但复杂度较高且频偏估计范围较小。邱天爽等[13]利用循环相关熵谱完成了频偏估计，但仅适用于bpsk信号。a.feder等[14]利用循环自相关性完成了符号速率和频偏的估计(本发明中简记为fcs)，但需高倍过采样信号与预知信号调制阶数，且对于高阶调制信号性能较差。a.feder等[15]利用循环统计特征完成了符号时延和载波相位的估计(本发明中简记为tcs)，但需高倍过采样信号与预知精确频偏，且对于高阶调制信号性能较差。

3、可见，常见算法[6]-[15]对符号时延与频偏这两个重要参数进行联合盲估计的研究极少，且监管方作为通信第三方通常无法预知辅助序列，因此本发明重点对时频混叠信号符号时延与频偏联合盲估计技术进行了研究。考虑到时频混叠信号与单载波信号具有相似的循环自相关性，因此本发明首先对基于循环自相关性的单载波信号符号时延与频偏估计技术进行了研究。wang等[16]在2002年给出了基于不同过采样倍数单载波信号循环自相关特征的符号时延与频偏盲估计算法，且循环自相关特征对调制方式不敏感的特点使得该算法适用于各类调制方式信号。后续，wang等在2003年[17]对循环自相关特征提取公式进行了进一步简化，完成了对两倍过采样单载波信号的符号时延盲估计。由于该算法[17]仅采用两类循环自相关特征导致估计精度不高，因此li等[18]于2022年在此[16][17]基础上给出了一种基于两倍过采样信号与四类循环自相关特征的单载波信号符号时延高精度估计算法。

4、同时，由于本发明所提技术需采用群智能优化算法进行矩阵求解运算，因此本发明在此对群智能优化算法领域相应背景技术进行概述。虽然目前适用于各领域的群智能优化算法层出不穷[19][20][21]，且各种群智能优化算法均具有求解复杂任务的能力，但由于本发明矩阵中的符号时延参数具有周期特性，无法直接计算出该参数对应种群个体间的实际差异，因此如差分进化算法[22]、指数分布优化算法[23]以及雪消融优化算法[24]等这类需计算种群个体间实际差异的群智能优化算法虽然在解决其他问题时性能良好，但却并不适用于求解本发明矩阵。而基于鸟群觅食思想的粒子群优化算法(particle swarmoptimization,pso)[25]，结构简单但性能不佳。基于显微镜放大思想的光学显微镜算法(optical microscope,om)[26]性能较好但复杂度较高。基于层流与湍流思想的水流优化器算法(water flow optimizer,wfo)[27]复杂度与pso算法无显著差异，而性能则与om算法基本相同。

5、引证文献：

6、[1]m.zheleva,c.r.anderson,m.aksoy,j.t.johnson,h.affinnih andc.g.depree,"radio dynamic zones:motivations,challenges,and opportunities tocatalyze spectrum coexistence,"in ieee communications magazine,vol.61,no.6,pp.156-162,june 2023.

7、[2]mark dankberg.paired carrier multiple access(pcma)for satellitecommunication[c].in:pacific telecommunications conference,honolulu,hawaii,1998.787～791

8、[3]杨洪娟,时统志,李博等.基于联合特征参数的卫星单-混信号调制识别研究[j].电子与信息学报,2022,44(10):3499-3506.

9、[4]federa,hirschbeck m,gerstackerw.blind estimation ofthe carrierpowers and snrs in pcma satellite signals by cyclic statistics[c]//milcom2022-2022ieee military communications conference(milcom).ro ckville,md,usa.ieee,2023:913-919.

10、[5]yang,y.,zhang,d.and peng,h.(2018),single-channel blind sourceseparation forpaired carrier multiple access signals.iet signal process.,12:37-41.

11、[6]瞿孟虹,何晓霜,游凌.同频混合信号参数联合最大似然递归估计[j].电子科技大学学报,2015,44(03):339-343+380.

12、[7]yang yong,zhang dongling,peng hua.frequency offset estimationofthe linear mixture of two co-frequency 8phase-shift keying modulatedsignals[j].signal processing,iet,2015,9(2):186-192.

13、[8]魏雪娟,杨勇,郭一鸣等.pcma系统中干扰信号的频偏与时延联合估计[j].通信学报,2017,38(02):173-182.

14、[9]b.song,j.li andp.chen,"estimation algorithm ofinterferencefrequency offset in pcma system,"2017ieee 2nd advanced informationtechnology,electronic and automation control conference(iaeac),chongqing,china,2017,pp.1094-1097.

15、[10]li,f.,qiu,z.,zha,x.,&li,t.(2023).blind estimation of modulationparameters for pcma signals using frame cyclic features.eurasip journal onadvances in signal processing,2023(1),95.

16、[11]曲阜平,熊涛,江桦等.基于信赖域法的同频混合qpsk信号时延估计算法[j].信息工程大学学报,2015,16(06):685-688+696.

17、[12]付君,彭华,郭一鸣等.一种非数据辅助pcma信号参数联合估计算法[j].信息工程大学学报,2018,19(05):574-579.

18、[13]邱天爽,陈兴,马济通等.基于循环相关熵谱的时频混叠信号载波频率估计方法[j].通信学报,2018,39(06):20-26.

19、[14]a.feder,w.wicke,m.hirschbeck and w.gerstacker,"blind symbol rateand frequency offset estimation for pcma signals via cyclic correlations,"globecom 2020-2020ieee global communications conference,taipei,taiwan,china,2020,pp.1-7.

20、[15]a.feder,w.gerstacker and m.hirschbeck,"blind symbol timing andcarrier phase estimation for pcma satellite signals via cyclic statistics,"2021ieee global communications conference(globecom),madrid,spain,2021,pp.01-07.

21、[16]yan wang,p.ciblat,e.serpedin and p.loubaton,"performance analysisof a class ofnondata-aided frequency offset and symbol timing estimators forflat-fadingchannels,"in ieee transactions on signal processing,vol.50,no.9,pp.2295-2305,sept.2002.

22、[17]yan wang,e.serpedin and p.ciblat,"an alternative blindfeedforward symbol timing estimator using two samples per symbol,"in ieeetransactions on communications,vol.51,no.9,pp.1451-1455,sept.2003.

23、[18]li shibao,wang shuqi,zhao chengsuo,et al.a non-data-aidedfeedforward timing estimator based on multiple cyclic correlations for short-term burst signals[j].ieee communications letters,2022,26:2166-2169.

24、[19]tang jun,liu gang,pan qingtao.a review on representative swarmintelligencealgorithms for solving optimization problems:applications andtrends[j].ieee/caa journal of automatica sinica,2021,8(10):1627-1643.

25、[20]p.w.shaikh,m.el-abd,m.khanafer and k.gao,"a review on swarmintelligence and evolutionary algorithms for solving the traffic signalcontrol problem,"in ieee transactions on intelligent transportation systems,vol.23,no.1,pp.48-63,jan.2022.

26、[21]b.a.s.emambocus,m.b.jasser and a.amphawan,"a survey on theoptimization of artificial neural networks using swarm intelligencealgorithms,"in ieee access,vol.11,pp.1280-1294,2023.

27、[22]r.storn,"differential evolution design of an iir-filter,"proceedings of ieee international conference on evolutionary computation,nagoya,japan,1996,pp.268-273.

28、[23]mohamed abdel-basset,doaa el-shahat,mohammed jameel,etal.exponential distribution optimizer(edo):a novel math-inspired algorithmfor global optimization and engineering problems[j].artificial intelligencereview,2023,56:9329-9400.

29、[24]lingyun deng,sanyang liu.snow ablation optimizer:a novelmetaheuristic technique for numerical optimization and engineering design[j].expert systems with applications,2023,225:120069.

30、[25]j.kennedy and r.eberhart,"particle swarm optimization,"proceedings of icnn'95-international conference on neural networks,perth,wa,australia,1995,pp.1942-1948vol.4.

31、[26]min-yuan cheng,moh nur sholeh.optical microscope algorithm:a newmetaheuristic inspired by microscope magnification for solving engineeringoptimization problems[j].knowledge-based systems,2023,279:110939.

32、[27]luo kaiping.water flow optimizer:a nature-inspired evolutionaryalgorithm for global optimization[j].ieee transactions on cybernetics,2022,52:7753-7764。

技术实现思路

1、本发明的目的在于克服了现有技术的不足，而提出一种单通道时频混叠信号符号时延与频偏联合盲估计方法，本发明的算法具有对信号采集设备要求低、无需预知辅助序列和对调制方式不敏感的优点，较适用于高阶调制大带宽时频混叠信号逐渐增多的实际通信环境。

2、本发明的目的是通过如下措施来实现的：一种单通道时频混叠信号符号时延与频偏联合盲估计方法，包括以下步骤：

3、步骤a、利用单通道时频混叠信号与单载波信号具有的相似循环自相关性，提出一种单通道时频混叠信号循环自相关特征提取技术；

4、步骤b、利用循环自相关特征提取技术与对应简化算法，提取简化后的四类单通道时频混叠信号循环自相关特征，并构建以符号时延与频偏为参量的循环自相关特征矩阵；

5、步骤c、利用改进型水流优化器完成对矩阵最优解的快速智能求解，优化器的搜索结果即为单通道时频混叠信号符号时延与频偏的联合盲估计结果。

6、上述的一种单通道时频混叠信号符号时延与频偏联合盲估计方法，步骤a中，单通道时频混叠信号循环自相关特征提取技术如下：

7、时频混叠信号xp由两路符号速率与滚降系数均相同的单载波信号x0和x1组合而成，接收到的时频混叠信号复基带过采样序列可表示为：

8、xp(kts)＝x0(kts)+x1(kts)+y(kts)  (1)

9、其中ts为采样周期；k为样点计数；y(kts)为加性高斯白噪声；xi(kts)(i＝0,1)为xi的第k个样点，展开为：

10、

11、其中hi为xi幅度；j为虚数单位；fi为xi载波频偏；为xi载波相偏；mi为xi成型滤波函数影响范围；为xi在mi内的符号序列，xi间符号序列统计独立；g为升余弦成型滤波函数；t为符号周期；ei∈[-0.5,0.5)为xi符号时延；

12、单载波信号时变自相关函数为时间周期函数，可表示为：

13、

14、其中t30为自相关时延大小；n为起始位置；m为任意整数；n为信号过采样倍数；e{·}为取均值处理；*为共轭运算，r(n；t)对应的傅里叶级数系数可表示为：

15、

16、其中l为符号数；k＝0,1,...,n-1；循环自相关特征理论值r(k；t)的实际计算结果可简化为：

17、

18、时频混叠信号时变自相关函数可表示为：

19、

20、由于符号序列统计独立，式(6)可进一步简化为：

21、

22、时频混叠信号时变自相关函数rp(n；t)也是时间周期函数，且可视为两路子信号时变自相关函数之和，则其对应傅里叶级数系数可表示为：

23、

24、与式(5)相似，rp(k；t)实际计算值可表示为：

25、

26、上述的一种单通道时频混叠信号符号时延与频偏联合盲估计方法，步骤b中，循环自相关特征矩阵构建方法如下：

27、所述式(9)不包含变量ei和fi，为求解ei和fi，需进一步构建以ei和fi为变量的等式；

28、式(4)可简化为：

29、

30、其中f为载波频偏；p为信号功率；d为成型滤波函数影响范围；vt为噪声项，当n＝2且k＝1时，忽略噪声项干扰，则式(10)可简化为：

31、

32、其中e为符号时延；g(·)为g(·)傅里叶变换结果；由于g(·)具有偶对称性质，因此c(1；t)为实函数，gc(·)为实偶函数，c(1；t)可简化为：

33、

34、其中a为成型滤波函数滚降系数；

35、因此式(11)可进一步表示为：

36、

37、将式(13)代入式(8)，则循环自相关特征rp(1；t)可展开为：

38、

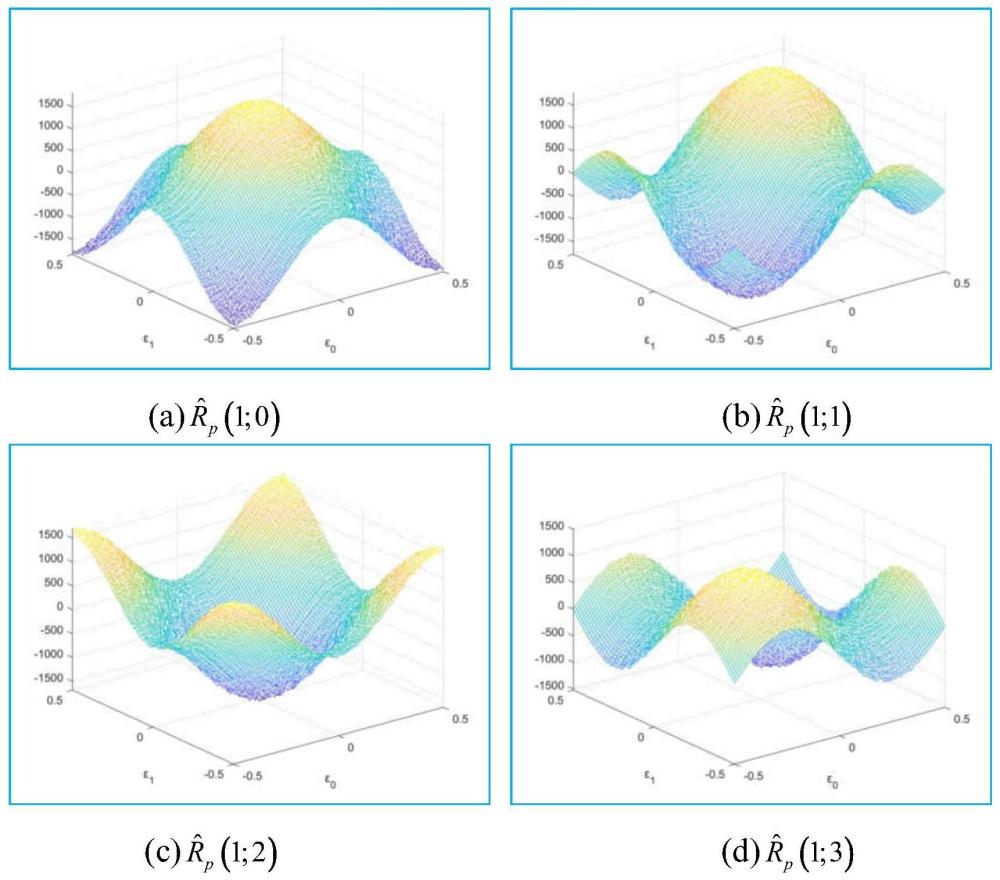
39、其中pi为xi平均功率；针对e0、e1、f0和f1等四个参数，构建t＝0,1,2,3时的四类循环自相关特征表达式，则式(14)可简化为：

40、

41、上述的一种单通道时频混叠信号符号时延与频偏联合盲估计方法，步骤c中，包括如下步骤：

42、联合式(9)与式(15)，当pi和a已知，可得群智能优化算法度量值计算公式为：

43、

44、其中||·||2表示l2-范数；

45、步骤c1、设定初始参数；设定粒子群pi，每组4维粒子群，i＝0,1,2,3分别对应参数e0、e1、f0和f1，最大迭代次数tm，粒子群大小np，pi取值上界ubi，pi取值下界lbi，层流形态概率pl以及涡流形态概率pe等参数值；

46、步骤c2、初始化粒子群状态；利用式(17)初始化粒子位置，利用式(16)计算粒子度量值并更新粒子群最佳位置和粒子群最佳度量值

47、pi＝lbi+ri·(ubi-lbi)  (17)

48、其中ri为[0,1]间均匀分布随机数；

49、步骤c3、区分层流形态与湍流形态；若[0,1]间均匀分布随机数r<pl，则认定本次迭代为层流形态，执行步骤4，否则为湍流形态，执行步骤5；

50、步骤c4、层流形态流动；以式(18)计算本次最大偏移量，以式(19)移动每组粒子，并以式(20)调整边界粒子位置，保证粒子群向最佳位置方向移动；

51、

52、

53、

54、其中tk为随机计数；pi,k为粒子群pi的第k组粒子；为临时粒子组；di每次迭代更新；

55、步骤c5、湍流形态流动；遍历每组粒子，令确定随机计数j1、j2和tk，且j11j2，tk1k；若r<pe，则认定水流为涡流形态，以式(21)移动粒子，并以式(20)调整边界粒子位置，否则认定为跃层形态，以式(22)移动粒子；

56、

57、

58、其中|·|表示取绝对值处理；

59、步骤c6、更新粒子群状态；利用式(16)计算对应临时度量值然后以式(23)更新pi,k与并更新和

60、

61、步骤c7、迭代搜索；若迭代次数t＝tm，则输出即为时频混叠信号的符号时延和频偏联合盲估计结果，否则再次执行步骤c3。

62、本发明的有益效果：本发明利用两倍过采样时频混叠信号的四类循环自相关特征构建了以符号时延和频偏为参数的循环自相关矩阵，同时为简化矩阵参数求解过程，利用改进型水流优化器算法(improved water flow optimizer,iwfo)完成了对矩阵最优解的快速搜索。相较于常见算法，本发明算法可利用两倍过采样信号完成对各类复杂调制方式组合时频混叠信号符号时延和频偏的高精度联合盲估计，且在高信噪比和高阶调制信号情况下具有至少1个数量级的估计精度优势。对信号采集设备要求低、无需预知辅助序列以及对调制方式不敏感的特点，使得该算法较适用于高阶调制大带宽时频混叠信号逐渐增多的实际通信环境。