一种面向区域受限频谱地图构建的传感器布局方法

本发明属于无线电监测，涉及一种面向区域受限频谱地图构建的传感器布局方法。

背景技术：

1、频谱资源在推动社会进步和确保国家安全防御中占据着举足轻重的地位。然而，随着频谱需求与供应之间的矛盾日益尖锐，频谱资源的稀缺性已成为无线通信领域亟待应对的严峻挑战之一。这电磁频谱地图作为一种重要工具，能够直观地展示目标区域的频谱信息，包括频率、时间、接收信号强度以及辐射源位置等关键数据，为频谱资源的管理和利用提供了有力的支持。电磁频谱地图的引入，能够直观地洞察目标区域的频谱使用状况及其变化趋势。这一技术有望在无线通信、雷达探测、辐射源定位、非法辐射源检测以及频谱资源调度等多个领域发挥至关重要的作用，为频谱资源的合理分配和高效利用做出重要贡献。

2、电磁频谱地图的构建，核心在于利用传感器对目标场景进行采样，获取频谱数据。然而采样过程面临着：采样的区域受限、采样点数目有限、采样时间有限等等困难。此外，已有实验验证了频谱地图的重构准确性不仅仅取决于采样点的数量，还与采样点所处的位置有着紧密的联系。因此，若能深入研究和充分利用空间频谱态势的内在特征，在采样区域受限的场景下，精准选择最优的传感器的布局位置以进行采样，便可以在采样数据需求相对较少的情况下成功构建出准确的频谱地图。

技术实现思路

1、针对上述技术问题，本发明提出了一种面向区域受限频谱地图构建的传感器布局方法。该方法基于压缩感知重建频谱环境地图的思想优化采样矩阵，在采样区域受限的情况下，获得最佳的传感器位置。通过该方法，本发明能够确定最少采样节点的数目和最优位置，从而在确保测绘性能最优的同时，实现节点的最小化使用。不仅能够提高频谱地图的测绘效率和准确性，还有助于降低系统成本，推动电磁频谱资源的合理利用和管理。

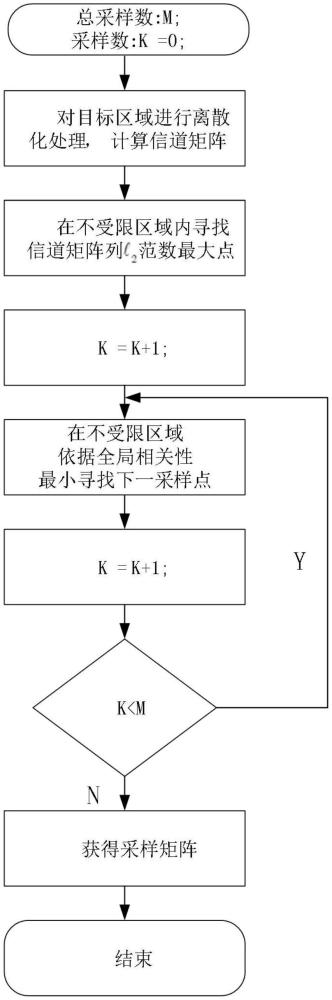
2、1一种面向区域受限频谱地图构建的传感器布局方法，其特征在于，包括下列步骤：

3、s1：将频谱地图对应的区域进行离散化处理；

4、s2：在不受限区域内，计算信道矩阵每列的范数，选取其最大的点作为第一个采样点；

5、s3：基于压缩感知的相关性约束条件，从采样矩阵和信道矩阵全局相关性最小的角度出发，在不受限区域内，使用贪婪算法进行采样点选取。

6、s4：进一步推导算法，简化贪婪算法运算。

7、2.根据权利要求1所述方法，其特征在于，步骤s1具体方法包括：

8、将频谱地图对应的区域按照比例分割为n＝nx×ny个正方形网格，其中nx表示x轴方向分割的网格数量，同理ny表示y轴方向分割的网格数量，n为总网格数，则所有的离散点位的集合可以表示为：u＝{u1,u2,…un}，假设有l个受限的区域，其受限位置的离散点位表示为：因此，不受限区域的离散点位集合是cvu，即u和v互为补集，频谱地图上任意区域的数据可以与网格组成的二维数据矩阵一一对应，即为

9、3.根据权利要求1上述方法，其特征在于，步骤s2具体方法包括：

10、s2.1：由信道传播模型可知，目标区域内每个网格点的接受信号强度是由各个辐射源经过路径损耗后进行线性叠加产生的，同时在目标区域内，辐射源的个数与总网格数n相比是稀疏的。对应的辐射源位置向量为：

11、

12、其中表示网格点ui处存在辐射源的功率大小，辐射源向量的稀疏度为：k＝||x||0；

13、s2.2考虑信号传输中的路径损耗与距离相关，则任意两个网格点的路径损耗函数表示为：

14、

15、其中：d0是参考距离，当辐射源与传感器之间的距离小于参考距离时不考虑路径损耗的影响，η为路径损耗因子，则整个区域内的信道矩阵为：

16、

17、其采样矩阵可以表示为：

18、φ＝[φ1,φ1,…,φm]t，

19、其中有且仅有一个非零元素且第i个传感器选择的位置uj∈cvu；

20、因此，频谱地图重构的问题完全可以看成压缩感知问题：

21、y＝φψx

22、即已知采样数据：y、采样矩阵φ、信道矩阵ψ，重构出辐射源向量x的过程；

23、s2.3从最大化矩阵行列式来优化采样矩阵的角度出发，在不受限区域内，选取信道矩阵中列2范数最大的点作为第一个采样点：

24、

25、4.根据权利要求1上述方法，其特征在于，步骤s3具体方法包括：

26、s4.1：现有研究表明，信道矩阵ψ与采样矩阵φ的相关性越低，压缩感知重构效果越好，采用下式定义相关性：

27、

28、其中：定义对矩阵列单位化，s＝φψ为感知矩阵，为s的每个列向量单位化，si和分别代表矩阵s和的第i个列向量；

29、但是，上述方法的缺点在于它主要聚焦于局部相关性的描述：例如，即使矩阵中仅有两列的内积较大，而其他列之间的内积均较小，这种情况虽然会导致局部相关系数偏高，但采样矩阵的实际性能可能并未受到显著影响，依然可以保持相对良好的表现。反之，另一种情况是矩阵中任意两列的内积都较为接近且数值不大，虽然表面上看来局部相关性不高，但整体相关系数可能较高，这种情况下采样矩阵的性能同样可能不会太好。因此，在评估采样矩阵性能时考虑全局的相关性特征，以获得更准确的评估结果。而且，由于感知矩阵进行了列单位化处理，每个列的自相关系数均为1，这意味着自相关的结果并不会对最终的求解产生实质性的影响，则全局相关性可以表述为：

30、

31、设gram矩阵则μall＝sum(g)，其中sum(·)表示矩阵中所有元素的和；目标转化为：选择合适的采样矩阵φ，使其与信道矩阵ψ的全局相关性最小。因此最小化并将采样位置求解为贪婪优化过程；

32、

33、s.t. |ω|＝m

34、在每次迭代过程，贪婪算法选择一个采样位置，并与先前已采样的位置结合时，使得相关性最小，如下式：

35、

36、重复直到确定m个采样点，表示经过i-1次迭代后的采样矩阵。

37、5.根据权利要求1所述方法，其特征在于，步骤s4具体方法包括：

38、定义其中b为a的列数，(x,x)表示其对角线元素。则任意矩阵d的列单位化：简化上述运算过程：

39、

40、其中：

41、

42、又因为：与互为转置矩阵：

43、

44、其中：

45、

46、由上述公式推导可得该部分的参数均为已知参数，在每次参与迭代的过程中仅需要计算一次。仅部分需要参与到迭代寻优中，简化了运算的过程。

47、有益效果

48、1)本方法基于压缩感知重建频谱环境地图的思想优化测量矩阵，在采样区域受限的情况下，以此获得最佳的传感器位置。通过该方法，本发明能够确定最少采样节点的数目和最优位置，在从而在确保测绘性能最优的同时实现传感器的最少使用。

49、2)本方法提出的传感器布局优化方案，使得采样矩阵和信道矩阵全局相关性最小，通过贪婪匹配的位置优化算法进行传感器位置选择，而且通过公式推导进一步简化了计算过程。