基于输出一致性的多弹协同制导方法与流程

本发明属于制导
技术领域：
，具体涉及基于输出一致性的多弹协同制导方法。
背景技术：
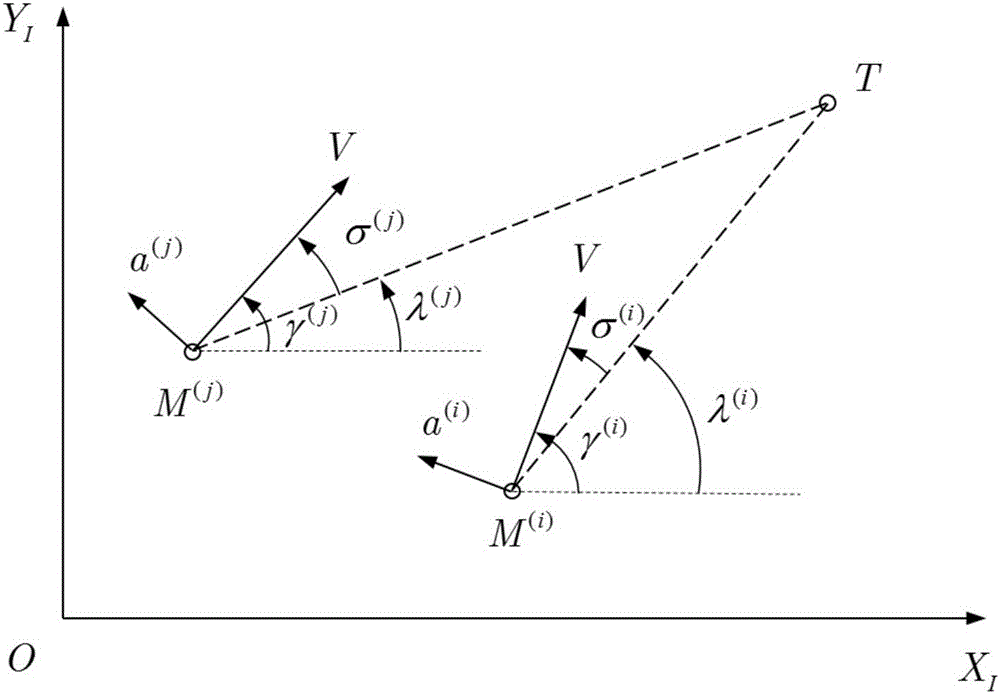
：随着导弹拦截系统的不断发展，依靠单弹突防、实现打击的战术逐渐受到限制。采用多枚导弹对同一目标实现饱和攻击，摧毁具有一定拦截能力目标的方法，已经成为了保证导弹战场生存能力、提高打击任务成功率的主要手段。从该思路出发，设计一种驱动多枚导弹同时命中目标的协同制导方法，对于突防技术的进步具有重要意义。现有的保证同时打击的协同制导方法，存在以下问题有待解决：1)单纯针对修正打击时间设计协同的制导方法难以保证精确命中目标，导引末端需要切换导引律以保证打击精度，而舍弃一定打击时间控制精度。此外，切换导引律导致系统复杂程度提高，出现非连续情况，不利于实施。2)协同制导要求各导弹同时命中目标，而导弹速度大小难以通过舵面控制，因此对于距离目标较近的导弹，需要绕行机动，延长命中时间。此举易导致弹道过于弯曲，在制导律设计时若不考虑视场角限制，则难以保证导引头视场始终捕获目标。3)由于导弹舵面偏转有限，导弹的法向加速度受到限制，导致导弹控制系统的输入具有饱和非线性。4)针对单一导弹设计命中时间控制制导律，而后指定命中时间的协同制导方法，未将导弹群作为整体考虑，无法实现最优的整体表现。综上所述，现有技术主要针对单一导弹设计命中时间控制制导律，而非将协同制导问题作为集群问题解决，且未考虑各种物理条件限制。技术实现要素：有鉴于此，本发明提供了基于输出一致性的多弹协同制导方法；本发明能够实现在法向过载及视场角受到限制情况下的最优协同制导。实现本发明的具体实施方案如下：基于输出一致性的多弹协同制导方法，具体步骤如下：步骤一、给定各导弹法向加速度和视场角的约束条件；步骤二、基于导弹和目标的相对运动关系，建立导弹状态依赖的线性模型，采用数值方法对所述导弹状态依赖的线性模型进行离散化，基于离散化后的导弹状态依赖的线性模型，根据设定的预测时域建立预测控制模型；步骤三、基于预测控制模型和各导弹打击时间协同的要求，获得性能指标函数；步骤四、基于二次规划形式，将性能指标函数和约束条件转化为二次规划标准型；步骤五、基于当前时刻各导弹状态、二次规划标准型的各导弹法向加速度和视场角的约束条件和性能指标函数，获得多弹协同制导的优化模型，基于多弹协同制导的优化模型，利用凸优化方法，获得当前时刻各导弹的最优控制序列；步骤六、从最优控制序列中选择各导弹的法向加速度并代入导弹状态依赖的线性模型，计算下一时刻的各导弹状态，按照步骤五的方式重复直至各导弹命中目标。进一步地，其特征在于，步骤一具体实现过程如下：定义编队中第i枚导弹的法向加速度约束条件为其中a(i)为第i枚导弹的法向加速度，为第i枚导弹的最大法向加速度；第i枚导弹的视场角的约束条件为σ(i)为第i枚导弹的速度前置角，为第i枚导弹的速度最大前置角。进一步地，步骤二具体实现过程如下：选取第i枚导弹的状态变量为第i枚导弹状态变量的变化率，第i枚导弹的控制变量u(i)＝a(i)，其中i,j＝1,...,Nv,i≠j，根据导弹和目标的相对运动关系，建立导弹状态依赖的线性模型：x·(i)=A(i)x(i)+B(i)u(i)y(i)=Cy(i)x(i)z1(i)=Cz1(i)x(i)z2(i)=Cz2(i)x(i)---(1)]]>其中a(i)表示第i枚导弹的法向加速度；A(i)为第i枚导弹的状态矩阵、B(i)为第i枚导弹的输入矩阵、y(i)、和分别为第i枚导弹的一致性变量、视线角速度和视场角，分别为第i枚导弹的一致性变量、视线角速度和视场角的输出矩阵，分别为r(i),λ(i),σ(i)对应的赋予变量，其表示形式分别如下：A(i)=01000000x1(i)x4(i)000010000-2x2(i)x1(i)000010,B(i)=0-x1(i)x4(i)V0x2(i)Vx1(i)-1V,]]>Cy(i)=kr00kr·000000,Cz1(i)=00010,Cz2(i)=00001.]]>r(i)表示第i枚导弹的弹目距离，表示第i枚导弹的弹目相对速度，λ(i)表示第i枚导弹的视线角，表示第i枚导弹的视线角速度，σ(i)为第i枚导弹的速度前置角，V表示导弹飞行速度，kr和分别为弹目距离的权重和弹目相对速度的权重；采用数值方法对状态矩阵A(i)、输入矩阵B(i)进行离散化，获得第i枚导弹的导弹状态依赖的线性模型的离散化形式定义k时刻导弹群整体状态变量X(k)，k时刻导弹群整体的一致性变量、视线角速度和视场角分别为Y(k)、Z1(k)、Z2(k)，控制变量U(k)，X(k)、Y(k)、Z1(k)、Z2(k)和U(k)分别为X(k)=[(x(1)(k))T,(x(2)(k))T,...,(x(Nv)(k))T]T]]>Y(k)=[(y(1)(k))T,(y(2)(k))T,...,(y(Nv)(k))T]T]]>Z1(k)=[(z1(1)(k))T,(z1(2)(k))T,...,(z1(Nv)(k))T]T]]>Z2(k)=[(z2(1)(k))T,(z2(2)(k))T,...,(z2(Nv)(k))T]T]]>U(k)=[(u(1)(k))T,(u(2)(k))T,...,(u(Nv)(k))T]T]]>其中，x(i)(k)为k时刻第i枚导弹状态变量；y(i)(k)为k时刻第i枚导弹的一致性变量；为k时刻第i枚导弹的视线角速度；为k时刻第i枚导弹的视场角；u(i)(k)为k时刻第i枚导弹的控制变量，i＝1,...,Nv；定义当前时刻导弹群整体状态矩阵当前时刻导弹群整体状态的一致性变量、视线角速度和视场角的输出矩阵分别为控制矩阵和分别为A‾=blkdiag(AD(1),AD(2),...,AD(Nv))]]>C‾y=blkdiag(Cy(1),Cy(2),...,Cy(Nv))]]>C‾z1=blkdiag(Cz1(1),Cz1(2),...,Cz1(Nv))]]>C‾z2=blkdiag(Cz2(1),Cz2(2),...,Cz2(Nv))]]>B‾=blkdiag(BD(1),BD(2),...,BD(Nv))]]>其中blkdiag为分块对角矩阵运算；定义预测控制模型的预测时域为N，获得预测时域内状态变量预测时域内导弹群整体状态的一致性变量、视线角速度和视场角的输出矩阵的输出变量分别为和控制变量状态矩阵控制矩阵预测时域内导弹群整体状态的一致性变量、视线角速度和视场角的输出矩阵的输出矩阵分别为和和分别为X~=[XT(k+1),XT(k+2),...,XT(k+N)]T]]>Y~=[YT(k+1),YT(k+2),...,YT(k+N)]T]]>Z~1=[Z1T(k+1),Z1T(k+2),...,Z1T(k+N)]T]]>Z~2=[Z2T(k+1),Z2T(k+2),...,Z2T(k+N)]T]]>U~=[UT(k),UT(k+2),...,UT(k+N-1)]T]]>C~y=IM⊗C‾y]]>C~z1=IM⊗C‾z1]]>C~z2=IM⊗C‾z2]]>其中IM为M阶单位矩阵，M＝N，为矩阵的克罗内克积运算；X(k+t)为k+t时刻导弹群整体的一致性变量，Y(k+t)为k+t时刻导弹群整体的视线角速度，Z1(k+t)为k+t时刻导弹群整体的视线角速度，Z2(k+t)为k+t时刻导弹群整体的视线视场角，U(k+t-1)为k+t-1时刻导弹群整体的控制变量；t＝1,...,N；选择所述导弹状态依赖的线性模型的一致性变量、视线角速度和视场角作为输出变量，基于预测时域内状态变量输出变量和控制变量状态矩阵控制矩阵输出矩阵和获得预测控制模型为X~=A~X(k)+B~U~Y~=C~yA~X(k)+C~yB~U~Z~1=C~z1A~X(k)+C~z1B~U~Z~2=C~z2A~X(k)+C~z2B~U~---(2)]]>其中，X(k)为k时刻导弹群整体状态变量。进一步地，所述数值方法为欧拉方法、改进欧拉方法、龙格-库塔法或线性多步法。进一步地，所述凸优化方法为二次规划方法。进一步地，步骤三具体实现过程如下：根据各导弹打击时间协同的要求，即将各导弹打击时间协同目标转化为各导弹弹目距离和弹目相对速度一致性目标、各导弹控制输入的优化和驱动各导弹命中目标，性能指标函数表达式为J＝J1+J2+J3(3)其中，J1为协同变量代价函数，J2为控制变量代价函数，J3为视线角速度代价函数，其分别为：J1=Σk=0NΣi=0NvΣj=0Nv(y(i)(k+1)-y(j)(k+1))TIm⊗aadj(ij)(y(i)(k+1)-y(j)(k+1))]]>J2=Σk=1NΣi=1Nvu(i)(k)R(i)u(i)(k)]]>J3=Σk=1NΣi=1Nvz1(i)(k+1)Q(i)z1(i)(k+1)]]>Im为m阶单位矩阵，u(i)(k)为k时刻第i枚导弹的控制变量，y(i)(k+1)为k+1时刻第i枚导弹的协同变量，为k+1时刻第i枚导弹的视线角速度，Nv为导弹总枚数，N为预测时域，R(i)、Q(i)为各导弹控制变量的权重和视线角速度的权重，为表示导弹通讯拓扑的邻接矩阵Aadj中的元素，定义扩展拉普拉斯矩阵为其中L为表示导弹通讯拓扑的拉普拉斯矩阵，L＝D-Aadj，D为入度矩阵，Im为m阶单位矩阵。定义导弹群整体的权重，和分别为协控制变量和视线角速度的整体权重R‾=diag(R(1),R(2),...,R(Nv))]]>Q‾=diag(Q(1),Q(2),...,Q(Nv))]]>基于扩展拉普拉斯矩阵和导弹群整体的权重，则预测时域上的拉普拉斯矩阵协控制变量权重和视线角速度权重分别为L~=IN⊗L‾R~=IN⊗R‾Q~=IN⊗Q‾---(4)]]>其中，IN为N阶单位矩阵，为矩阵的克罗内克积运算；基于预测控制模型，将式(4)带入式(3)，获得性能指标函数JJ=Σkk+N-1||Y(k+1)||L‾2+||U(k)||R‾2+||Z1(k+1)||Q‾2=||Y~||L~2+||U~||R~2+||Z~1||Q~2---(5)]]>其中为加权范数运算，进一步地，其特征在于，步骤四具体实现过程如下：基于性能指标函数，作如下变换：J=||Y~||L~2+||U~||R~2+||Z~1||Q~2=U~THU~+2U~TF+constant---(6)]]>其中H、F、constant分别为二次项系数、一次项系数和常数项，有H=B~T(C~yTL~C~y+C~z1TQ~C~z1)B~+R~]]>F=B~T(C~yTL~C~y+C~z1TQ~C~z1)A~X(k)]]>costant=(C~yA~X(k))TL~C~yA~X(k)+(C~z1A~X(k))TQ~C~z1A~X(k)]]>和均为预测时域内输出变量、为预测时域内控制变量，状态矩阵控制矩阵和分别为预测时域内输出矩阵；为加权范数运算，针对各导弹法向加速度约束条件依据二次规划形式，则二次规划标准型为ΛuU~≤U~max---(7)]]>其中Λu=INNv-INNv,U~max=1N⊗[amax(1),...,amax(Nv)]T-1N⊗[amax(1),...,amax(Nv)]T]]>其中为N×Nv阶单位矩阵；1N为N×1列向量；为第i枚导弹的最大法向加速度；u(i)为第i枚导弹的控制变量；X(k)为k时刻导弹群整体的一致性变量；Umax为预测时域内控制变量；针对各导弹视场角约束条件依据二次规划形式，则二次规划标准型为Λz1U~≤Z~1max---(8)]]>其中Λz1=Cz1B-Cz1B,Z~1max=-Cz1AX(k)+1N⊗[σmax(1),...,σmax(Nv)]TCz1AX(k)-1N⊗[σmax(1),...,σmax(Nv)]T]]>其中，σ(i)为第i枚导弹的速度前置角，为第i枚导弹的最大速度前置角,i＝1,...,Nv。有益效果：(1)本发明基于预测控制模型和各导弹打击时间协同的要求，将各导弹打击时间协同目标转化为各导弹弹目距离和弹目相对速度一致性目标，即同时命中的协同制导问题转化为各导弹弹目距离与弹目相对速度一致性问题，避免了对剩余时间的估计以及制导律切换等问题，便于实现。(2)本发明采用模型预测控制对导弹群整体建立模型，并设计控制律，可保证整体最优性。(3)本发明基于二次规划的求解方式易于在控制指令生成时引入约束条件限制(如法向加速度、视场角)，更贴近实际制导环境。附图说明图1为基于输出一致性的多弹协同制导方法流程图。图2为弹目相对关系几何图。图3为弹道轨迹图。图4为法向加速度曲线图。图5为视场角曲线图。图6为视线角速度曲线图。图7为剩余命中时间曲线图。图8为最大剩余命中时间误差曲线图。具体实施方式下面结合附图并举实施例，对本发明进行详细描述。本发明提供了基于输出一致性的多弹协同制导方法。其基本思想在于：将各导弹命中时间一致的要求在连续的控制指令形成过程中转化为各导弹弹目距离和各导弹弹目相对速度趋于一致的要求，从而达到各导弹命中时间相同的协同制导控制目标。在制导过程中，本发明采用模型预测控制的方式形成控制指令，使得导弹群整体性能表现最优化，并且能够实现对法向过载和视场角的限制。具体实现步骤如下：步骤一：给定不同导弹法向加速度和视场角的约束条件；如法向加速度、视场角等。对于不同类型的导弹，可给出不同的约束条件。定义编队中第i枚导弹的法向加速度约束条件为其中a(i)为第i枚导弹的法向加速度。设计视场角时，假设导弹侧滑角较小且可忽略，将视场角近似为导弹速度前置角σ，则给出第i枚导弹的视场角的约束条件为σ(i)为第i枚导弹的速度前置角。步骤二：基于导弹和目标的相对运动关系，建立导弹状态依赖的线性模型，根据导弹状态依赖的线性模型，选择所述模型的一致性变量、视线角速度和视场角作为输出变量，采用数值方法对所述导弹状态依赖的线性模型进行离散化，基于离散化后的导弹状态依赖的线性模型，根据设定的预测时域建立预测控制模型。二维平面内导弹群攻击目标的几何关系如图1所示，其中M(i)、M(j)、T分别表示第i枚导弹、第j枚导弹、攻击目标，上标(i)、(j)分别表示第i枚导弹、第j枚导弹对应的状态，i,j＝1,...,Nv,i≠j，Nv为导弹总枚数，a表示导弹法向加速度。选择所述导弹状态依赖的线性模型的一致性变量、视线角速度和视场角作为输出变量，选取第i枚导弹的状态变量为第i枚导弹状态变量的变化率，第i枚导弹的控制变量u(i)＝a(i)，其中i,j＝1,...,Nv,i≠j，根据导弹和目标的相对运动关系，建立导弹状态依赖的线性模型：x·(i)=A(i)x(i)+B(i)u(i)y(i)=Cy(i)x(i)z1(i)=Cz1(i)x(i)z2(i)=Cz2(i)x(i)---(1)]]>其中a(i)表示第i枚导弹的法向加速度；A(i)为第i枚导弹的状态矩阵、B(i)为第i枚导弹的输入矩阵、y(i)、和分别为第i枚导弹的一致性变量、视线角速度和视场角，分别为第i枚导弹的一致性变量、视线角速度和视场角的输出矩阵，分别为r(i),λ(i),σ(i)对应的赋予变量，其表示形式分别如下：A(i)=01000000x1(i)x4(i)000010000-2x2(i)x1(i)000010,B(i)=0-x1(i)x4(i)V0x2(i)Vx1(i)-1V,]]>Cy(i)=kr00kr·000000,Cz1(i)=00010,Cz2(i)=00001.]]>r(i)表示第i枚导弹的弹目距离，表示第i枚导弹的弹目相对速度，表示第i枚导弹的视线角速度，σ(i)为第i枚导弹的速度前置角，V表示导弹飞行速度，kr和分别为弹目距离的权重和弹目相对速度的权重；λ(i)表示第i枚导弹的视线角。采用数值方法对状态矩阵A(i)、输入矩阵B(i)进行离散化，获得第i枚导弹的导弹状态依赖的线性模型的离散化形式定义k时刻导弹群整体状态变量X(k)，k时刻导弹群整体的一致性变量、视线角速度和视场角分别为Y(k)、Z1(k)、Z2(k)，控制变量U(k)，X(k)、Y(k)、Z1(k)、Z2(k)和U(k)分别为X(k)=[(x(1)(k))T,(x(2)(k))T,...,(x(Nv)(k))T]T]]>Y(k)=[(y(1)(k))T,(y(2)(k))T,...,(y(Nv)(k))T]T]]>Z1(k)=[(z1(1)(k))T,(z1(2)(k))T,...,(z1(Nv)(k))T]T]]>Z2(k)=[(z2(1)(k))T,(z2(2)(k))T,...,(z2(Nv)(k))T]T]]>U(k)=[(u(1)(k))T,(u(2)(k))T,...,(u(Nv)(k))T]T]]>其中，x(i)(k)为k时刻第i枚导弹状态变量；y(i)(k)为k时刻第i枚导弹的一致性变量；为k时刻第i枚导弹的视线角速度；为k时刻第i枚导弹的视场角；u(i)(k)为k时刻第i枚导弹的控制变量，i＝1,...,Nv；定义当前时刻导弹群整体状态矩阵当前时刻导弹群整体状态的一致性变量、视线角速度和视场角的输出矩阵分别为控制矩阵和分别为A‾=blkdiag(AD(1),AD(2),...,AD(Nv))]]>C‾y=blkdiag(Cy(1),Cy(2),...,Cy(Nv))]]>C‾z1=blkdiag(Cz1(1),Cz1(2),...,Cz1(Nv))]]>C‾z2=blkdiag(Cz2(1),Cz2(2),...,Cz2(Nv))]]>B‾=blkdiag(BD(1),BD(2),...,BD(Nv))]]>其中blkdiag为分块对角矩阵运算。定义预测控制模型的预测时域为N，获得预测时域内状态变量预测时域内导弹群整体状态的一致性变量、视线角速度和视场角的输出矩阵的输出变量分别为和控制变量状态矩阵控制矩阵预测时域内导弹群整体状态的一致性变量、视线角速度和视场角的输出矩阵的输出矩阵和和分别为X~=[XT(k+1),XT(k+2),...,XT(k+N)]T]]>Y~=[YT(k+1),YT(k+2),...,YT(k+N)]T]]>Z~1=[Z1T(k+1),Z1T(k+2),...,Z1T(k+N)]T]]>Z~2=[Z2T(k+1),Z2T(k+2),...,Z2T(k+N)]T]]>U~=[UT(k),UT(k+2),...,UT(k+N-1)]T]]>C~y=IM⊗C‾y]]>C~z1=IM⊗C‾z1]]>C~z2=IM⊗C‾z2]]>其中IM为M阶单位矩阵，M＝N，为矩阵的克罗内克积运算；X(k+t)为k+t时刻导弹群整体的一致性变量，Y(k+t)为k+t时刻导弹群整体的视线角速度，Z1(k+t)为k+t时刻导弹群整体的视线角速度，Z2(k+t)为k+t时刻导弹群整体的视线视场角，U(k+t-1)为k+t-1时刻导弹群整体的控制变量；t＝1,...,N；选择所述导弹状态依赖的线性模型的一致性变量、视线角速度和视场角作为输出变量，基于预测时域内状态变量输出变量和控制变量状态矩阵控制矩阵输出矩阵和获得预测控制模型为X~=A~X(k)+B~U~Y~=C~yA~X(k)+C~yB~U~Z~1=C~z1A~X(k)+C~z1B~U~Z~2=C~z2A~X(k)+C~z2B~U~---(2)]]>其中，X(k)为k时刻导弹群整体状态变量。步骤三：基于预测控制模型和各导弹打击时间协同的要求，获得性能指标函数。根据各导弹打击时间协同的要求，即将各导弹打击时间协同目标转化为各导弹弹目距离和弹目相对速度一致性目标、各导弹控制输入的优化和驱动各导弹命中目标，性能指标函数表达式为J＝J1+J2+J3(3)其中J1=Σk=0NΣi=0NvΣj=0Nv(y(i)(k+1)-y(j)(k+1))TIm⊗aadj(ij)(y(i)(k+1)-y(j)(k+1))]]>J1为协同变量代价函数，用于保证各导弹的弹目距离趋于一致且弹目相对速度趋于一致，J2=Σk=1NΣi=1Nvu(i)(k)R(i)u(i)(k)]]>J2为控制变量代价函数，用于优化控制输入，J3=Σk=1NΣi=1Nvz1(i)(k+1)Q(i)z1(i)(k+1)]]>J3为视线角速度代价函数，用于驱动各导弹视线角速度归零，保证命中目标。其中，Im为m阶单位矩阵，u(i)(k)为k时刻第i枚导弹的控制变量，y(i)(k+1)为k+1时刻第i枚导弹的协同变量，为k+1时刻第i枚导弹的视线角速度，Nv为导弹总枚数，N为预测时域，R(i)、Q(i)为各导弹控制变量的权重和视线角速度的权重，为表示导弹通讯拓扑的邻接矩阵Aadj中的元素，定义扩展拉普拉斯矩阵为其中L为表示导弹通讯拓扑的拉普拉斯矩阵，L＝D-Aadj，D为入度矩阵，定义导弹群整体的权重，和分别为协控制变量和视线角速度的整体权重R‾=diag(R(1),R(2),...,R(Nv))]]>Q‾=diag(Q(1),Q(2),...,Q(Nv))]]>基于扩展拉普拉斯矩阵和导弹群整体的权重，则预测时域上的拉普拉斯矩阵协控制变量权重和视线角速度权重分别为L~=IN⊗L‾R~=IN⊗R‾Q~=IN⊗Q‾---(4)]]>基于预测控制模型，将式(4)带入式(3)，获得性能指标函数J=Σkk+N-1||Y(k+1)||L‾2+||U(k)||R‾2+||Z1(k+1)||Q‾2=||Y~||L~2+||U~||R~2+||Z~1||Q~2---(5)]]>其中为加权范数运算。步骤四：基于性能指标函数和约束条件，依据二次规划形式转化为二次规划标准型。基于性能指标函数，作如下变换：J=||Y~||L~2+||U~||R~2+||Z~1||Q~2=U~THU~+2U~TF+constant---(6)]]>其中H、F、constant分别为二次项系数、一次项系数和常数项，有H=B~T(C~yTL~C~y+C~z1TQ~C~z1)B~+R~]]>F=B~T(C~yTL~C~y+C~z1TQ~C~z1)A~X(k)]]>costant=(C~yA~X(k))TL~C~yA~X(k)+(C~z1A~X(k))TQ~C~z1A~X(k)]]>和均为预测时域内输出变量、为预测时域内控制变量，状态矩阵控制矩阵和分别为预测时域内输出矩阵；为加权范数运算，针对各导弹法向加速度约束条件依据二次规划形式，则二次规划标准型为ΛuU~≤U~max---(7)]]>其中Λu=INNv-INNv,U~max=1N⊗[amax(1),...,amax(Nv)]T-1N⊗[amax(1),...,amax(Nv)]T]]>其中为N×Nv阶单位矩阵；1N为N×1列向量；为第i枚导弹的最大法向加速度；u(i)为第i枚导弹的控制变量；X(k)为k时刻导弹群整体的一致性变量；Umax为预测时域内控制变量；Λu为和组成的矩阵。针对各导弹视场角约束条件依据二次规划形式，则二次规划标准型为Λz1U~≤Z~1max---(8)]]>其中Λz1=Cz1B-Cz1B,Z~1max=-Cz1AX(k)+1N⊗[σmax(1),...,σmax(Nv)]T-Cz1AX(k)+1N⊗[σmax(1),...,σmax(Nv)]T]]>其中，σ(i)为第i枚导弹的速度前置角(即视场角)，为第i枚导弹的最大速度前置角(即最大视场角),i＝1,...,Nv；为由和组成的矩阵。步骤五：基于当前时刻各导弹状态、二次规划标准型的各导弹法向加速度和视场角的约束条件和性能指标函数，获得多弹协同制导的优化模型，利用凸优化方法(二次规划方法)，获得当前时刻各导弹的最优控制序列，即为系统输入量。基于二次规划标准型的当前时刻各导弹状态、各导弹法向加速度和视场角的约束条件、性能指标函数，获得多弹协同制导的优化模型：subjecttominU~J=U~THU~+2U~TFΛuU~≤U~maxΛz1U~≤Z~1max]]>步骤六、从最优控制序列中选择各导弹的法向加速度并代入导弹状态依赖的线性模型，计算下一时刻的各导弹状态，按照步骤五的方式重复直至各导弹命中目标。本发明采用在线二次规划方法寻求最优解，但寻优方法不仅限于此。得到最优控制序列后，将其首向U(k)作为各导弹的输入量，输入制导系统，完成闭环，并采样得到下一时刻的各导弹的状态：视线角λ(i)(k+1)、速度前置角σ(i)(k+1)、航向角θ(i)(k+1)、弹目距离r(i)(k+1)，计算得到x(i)(k+1)，作为初值，再进行下一时刻的优化问题求解，给出控制指令，重复该过程直到各导弹命中目标。实施例：实例场景为4枚导弹组成的导弹群攻击一静止目标，目标位置和各导弹位置、初始速度前置角如表1所示表1导弹、目标初始运动参数位置(千米)初始速度前置角(°)导弹1(4.5528,-3.7266)14.3239导弹2(2.9435,-1.4304)11.4592导弹3(2.9793,3.8354)-22.9183导弹4(5.2758,5.9533)-5.7296目标(10,0)设置各导弹法向加速度限制为50米/秒2，视场角限制为0.75弧度，并假设各导弹速度为300米/秒。选择模型预测控制预测时域N＝20，选择权重Q(i)＝1R(i)＝0.23、kr＝0.67、导弹间的通讯拓扑为连通无向图。采用本发明实现4枚导弹同时打击一静止目标的弹道和各运动状态变化曲线如图3-8所示。综上所述，以上仅为本发明的较佳实施例而已，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。当前第1页1 2 3