一种获取高精度的快中子反应堆组件少群截面的方法与流程

本发明涉及核反应堆堆芯设计和核反应堆物理计算领域，具体涉及一种获取高精度的快中子反应堆组件少群截面的方法。

背景技术：

目前快堆的发展处于预设计及实验阶段，为了快速、精确地求解堆芯中子学参数，基于“两步法”的方法成为快堆工程计算的主要方法。所谓“两步法”，第一步是对堆芯内各种组件材料进行多群中子输运计算，获得组件内的中子通量密度分布从而归并出少群均匀化群截面；第二步是由前一步计算得到的均匀化参数对堆芯进行少群中子输运方程的求解，获取堆芯有效增殖因子、堆芯功率分布等物理量。

在快堆中，不锈钢、液态金属钠等材料是较为常见并且大量存在的材料，这些核素的弹性散射截面具有极强的弹性散射共振效应。由于存在弹性散射共振的能量区域正是快中子反应堆中子通量密度分布集中的区域，必须精确考虑此效应。此外，由于引起裂变反应的为快中子，并且阈能反应具有与弹性散射截面相同量级的截面值，阈能反应也应重视；最后，不仅重核素有共振效应，中等原子质量的核素也具有共振效应，材料内多核素的共振干涉效应也应重点考虑。所谓共振干涉效应，指的是两个或两个以上具有共振效应的核素，其共振峰相互重叠造成的影响。

另一方面，快中子具有较长的平均自由程，其局部非均匀效应很弱，在组件的能谱计算中考虑均匀问题就可以获得足够高的精度。所谓非均匀效应，是指由于空间内不同介质如燃料和冷却剂的截面值不同，不同介质内中子通量分布具有显著的差异。

目前，“两步法”在热堆(如压水堆)已被广泛应用并得到工业界的认可，并有非常成熟的计算软件。但由于快堆与热堆在中子特性上存在极大区别，这些程序所采用的方法是不适于快中子反应堆的计算的，因此需要开发一种可以获取高精度的快中子反应堆少群截面的方法。

技术实现要素：

为了克服上述现有技术存在的问题，本发明的目的在于提供一种获取高精度的快中子反应堆组件少群截面的方法，为了获得精确的快中子堆组件少群截面，本发明方法将基于点截面信息计算组件内中子通量密度分布，以此进行能群归并获得少群截面参数，它能够高效、精准地计算出组件少群截面的参数，为堆芯中子学计算提供可靠的数据。

为了实现以上目的，本发明采取如下的技术方案：

一种获取高精度的快中子反应堆组件少群截面的方法，包括如下步骤：

步骤1：针对所需计算的任一快堆组件，读取多群数据库中信息，包括总截面、非弹性散射截面矩阵、中子裂变谱、每次裂变释放中子数，利用公式(2)计算组件的宏观非弹性散射矩阵，利用公式(3)计算各个核素的稀释截面值；

式中：

——第g群到第g’群的宏观非弹性散射截面矩阵

N_i——第种核素的核子密度

——第种核素第g群到第g’群的非弹性散射截面矩阵

g g′——细群能群标识号

式中：

——核素的稀释截面

——核素微观总截面

N_j——核素的核子密度

步骤2：针对所需计算的任一快堆组件，读取点截面数据库信息，包括总截面、弹性散射截面、裂变截面及不可分辨共振区的插值表，利用公式(5)计算出细群的微观平均总截面、微观平均总弹性散射截面、微观平均裂变截面，利用步骤1中计算得到的每个核素的稀释截面按照数据库提供的插值表进行插值；

式中：

——第g群的平均截面，x为反应类型

Σ^t——系统的宏观总截面

ΔE_g——第g群的能群区间

步骤3：由步骤2提供的各个核素的微观平均总弹性散射截面，利用公式(8)计算各个核素的弹性散射截面矩阵，利用公式(10)计算宏观弹性散射截面矩阵，并与步骤1计算得到的宏观非弹性散射截面矩阵加和，利用公式(11)计算宏观散射截面矩阵；

式中：

——第l阶由第g群散射到第g’群的弹性散射截面

σ_s,g——第g群的弹性散射截面

α——(A-1)²/(A+1)²，A为核素的原子质量

μ_c——质心坐标系下的散射角余弦值

f(E,μ_c)——散射概率函数

P_l(μ_s)——关于μ_s的阶勒让德多项式

μ_s——实验室坐标系下的散射角余弦值

式中：

——第l阶第g群到第g’群的宏观弹性散射截面矩阵

——第l阶第种核素第g群到第g’群的弹性散射截面矩阵

式中：

——第l阶第g群到第g’群的宏观散射截面矩阵

步骤4：由步骤2及步骤3获得快堆组件的微观平均总截面、宏观散射截面矩阵、微观平均裂变截面，利用公式(12)进行中子输运方程的求解，获得细群的中子通量分布，利用求得的中子通量分布使用公式(13)及(14)进行截面的能群归并，获得具有高精度的少群截面值；

式中：

B——系统的临界曲率

χ_g——第g群的中子裂变谱

υ——每次裂变释放中子数

k_eff——系统的有效增殖因子

——第g群的阶中子通量密度分布

$A_n=b_{n-1}+\frac{a_n}{A_{n+1}}$

$a_n=\frac{n+1}{2n+1}\frac{n+1}{2(n+1)+1}{B}^2$

$b_n={\mathrm{\Σ}}_t-{\mathrm{\Σ}}_s^{n+1}$

式中：

G——少群能群标识号

——属于第G少群的细群g。

与现有技术相比，本发明有如下突出的优点：

1.利用点截面数据库制作快堆组件的细群截面的流程，精细考虑了中等质量核素在中高能量区间存在的非常强烈的弹性散射共振效应以及所有核素在全能量段具有的共振干涉效应。

2.在由点截面归并为细群截面时，提供了该问题真实的中子通量密度分布。

3.计算快堆组件的细群中子通量密度分布并以此归并截面，即节省计算时间，又具有足够的精度。

附图说明

图1是利用点截面计算少群截面的流程图。

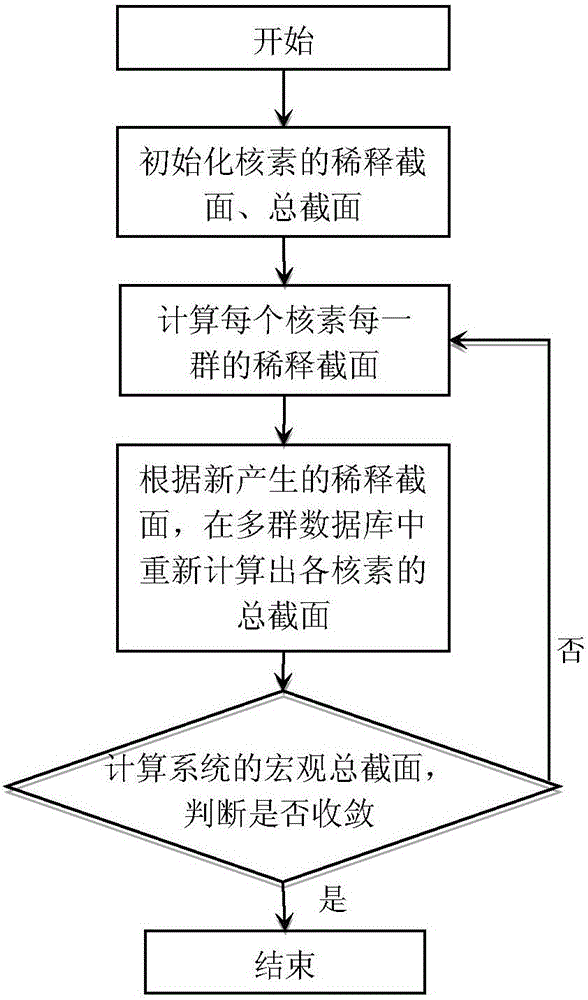
图2是迭代求解核素稀释截面示意图。

图3是26群宏观总截面及其误差。

具体实施方式

下面结合附图和具体实施方式对本发明作进一步详细说明：

本发明通过直接使用点截面文件，精细考虑快堆组件中存在的共振效应，进行均匀问题中子输运方程的求解，获得组件的真实中子通量分布，以此进行能群归并，从而获得精确的少群截面参数，如图1所示，该发明包括如下步骤：

步骤1：针对所需计算的任一快堆组件，读取多群数据库中信息，包括总截面、非弹性散射截面、中子裂变谱、每次裂变释放中子数，随后首先对截面进行温度插值，其中，截面的温度插值遵循规律，如公式(1)所示：

式中：

σ——截面

x——反应类型，如总截面

T——温度

下标3——被插值温度点

下标1、2——插值温度点

利用插值得到的特定温度下各核素的非弹性散射矩阵，利用公式(2)计算得到组件的宏观非弹性散射矩阵。

式中：

——第g群到第g’群的宏观非弹性散射截面矩阵

N_i——第种核素的核子密度

——第种核素第g群到第g’群的非弹性散射截面矩阵

随后，计算各个核素的稀释截面值，对于核素，其稀释截面由公式(3)定义。

式中：

——核素的稀释截面

——核素微观总截面

N_j——核素的核子密度

公式(3)中稀释截面是由其它核素的总截面决定的，而该核素的稀释截面确定后又会重新得到该稀释截面下的总截面值，整个过程需要进行迭代计算，当最终该问题的总宏观截面几乎不变化时认为迭代收敛。稀释截面计算的迭代流程如图2所示：

1)初始化所有核素的稀释截面的初始值，按照此初始稀释截面值按照公式(4)进行插值计算，得到每个核素的总截面值；

2)根据每个核素的新的总截面值，再利用公式(3)计算所有核素新的稀释截面值；

3)再由新产生的稀释截面之按照公式(4)计算总截面值；

4)当两次计算的总截面相对偏差小于0.000001时即认为计算收敛，否则继续进行计算。

公式(4)给出log-log插值律。

式中：

σ^x——某一反应的截面，如总截面

σ⁰——稀释截面

下标3——被插值点

下标1、2——插值点

步骤2：针对所需计算的任一快堆组件，读取点截面数据库信息，包括总截面、弹性散射截面、裂变截面及不可分辨共振区的插值表；对于位于不可分辨共振区的截面，利用步骤1计算收敛后得到的各核素的稀释截面，可以通过插值的方式计算出每个核素在不可分辨共振区的总截面、裂变截面、弹性散射截面，从而得到所有核素全能量段的点截面信息。由于各核素点截面中能量点的个数不相同，因此将每个核素的点截面在全能量段进行线性插值计算，得到相等能量点下的点截面值。基于窄共振近似，各核素的多群截面可由公式(5)确定。所谓窄共振近似，是指共振峰的宽度足够窄，窄到小于中子发生弹性散射后损失的能量宽度。

式中：

——第g群的平均截面，x为反应类型，如总截面等

Σ^t——系统的宏观总截面

ΔE_g——第g群的能群区间

利用公式(5)即可计算出细群的平均总截面、平均总弹性散射截面、平均裂变截面；

步骤3：由步骤2提供的各个核素的微观平均总弹性散射截面值，利用公式(8)计算各个核素的弹性散射截面矩阵，利用公式(10)计算该问题的宏观弹性散射截面矩阵，并与步骤1计算得到的宏观非弹性散射截面矩阵加和，利用公式(11)计算宏观散射截面矩阵；

一般的，入射能量为的中子发生弹性散射反应后，出射中子能量为时散射截面可由下式确定：

式中：

σ_s(E→E′)——由能量点E散射到能量点E’的弹性散射截面

α——(A-1)²/(A+1)²，A为核素的原子质量

μ_c——质心坐标系下的散射角余弦值

f(E,μ_c)——散射概率函数

对公式(6)进行能群上的积分，即可得到群到群的弹性散射截面，如下式：

式中：

φ_g——第g群的中子通量密度分布

严格求解公式(7)将消耗较多的时间，在细群多群结构的基础上，可引入近似，认为中子通量密度及截面在某一能群上是常数，那么公式(7)可简化为：

式中：

σ_s(g→g′)——由第g群散射到第g’群的弹性散射截面

σ_s,g——第g群的弹性散射截面

当弹性散射截面按照勒让德多项式展开后，其各阶的散射截面可表示为：

式中：

——第阶散射截面

P_l(μ_s)——关于μ_s的阶勒让德多项式

μ_s——实验室坐标系下的散射角余弦值

最终根据公式(9)，可得到所有核素的各阶弹性散射截面矩阵，由此利用公式(10)计算出系统的各阶宏观弹性散射截面矩阵，再加上由步骤2计算得到的宏观非弹性散射截面矩阵，利用公式(11)即可得到系统的宏观散射截面矩阵。

式中：

——第l阶第g群到第g’群的宏观弹性散射截面矩阵

——第l阶第种核素第g群到第g’群的弹性散射截面矩阵

式中：

——第l阶第g群到第g’群的宏观散射截面矩阵

步骤4：由步骤2及步骤3获得快堆组件的微观平均总截面、宏观散射截面矩阵、微观平均裂变截面，针对所计算的快堆组件，利用公式(12)求解多群中子输运方程即可得到该问题的细群多群中子通量密度分布：

式中：

B——系统的临界曲率

χ_g——第g群的中子裂变谱

υ——每次裂变释放中子数

k_eff——系统的有效增殖因子

——第g群的阶中子通量密度分布

$A_n=b_{n-1}+\frac{a_n}{A_{n+1}}$

$a_n=\frac{n+1}{2n+1}\frac{n+1}{2(n+1)+1}{B}^2$

$b_n={\mathrm{\Σ}}_t-{\mathrm{\Σ}}_s^{n+1}$

获得中子通量密度分布后，再经过能群归并，最终可得到该快堆组件的少群组件截面参数。利用中子通量密度作为权重归并少群截面参数的计算可由公式(13)、(14)得出。其中，公式(13)用来归并总截面、中子产生截面，公式(14)用来归并阶的散射矩阵。

式中：

G——少群能群标识号

——属于第G少群的细群g

图3展示了利用本发明计算得到的一快堆组件26群宏观总截面与使用蒙特卡洛方法计算出的26群截面以及两者之间的误差。初步的计算结果表明，利用本发明计算得到的少群截面与参考解相比，几乎全部能群的截面相对误差在1％以内，在能量较低的个别能群，误差控制在3％以内。由于能量较低处的中子通量密度分布也很低，这个误差是可接受的。利用准确的少群截面，就可以进行快堆堆芯的各种中子学计算，如稳态计算、燃耗计算、瞬态计算等。本发明既可得到很高的精度，同时计算效率要远远高于蒙卡方法，可应用于实际的工程计算当中。