基于LaserTRACER的数控机床平动轴几何误差检测与辨识方法与流程

本发明属于数控机床几何误差精密测量与辨识技术领域，特别是涉及一种基于LaserTRACER的数控机床平动轴几何误差检测与辨识方法。

背景技术：

误差补偿是提高数控机床几何精度的一种有效手段，而数控机床三个平动轴的误差检测和辨识是误差补偿最为基础的一部分。目前应用最为广泛的数控机床误差检测方法有两类：一类是基于激光干涉仪的单项误差直接测量法，此方法虽测量结果准确，但需要经验丰富的工程技术人员多次精准调试干涉仪镜组的位置分别测量各项误差，自动化程度低，耗时较长。另一类是间接误差辨识法，其中应用最广的是“9线法”和“球杆仪法”，两者均可快速辨识出机床的全部几何误差。但“9线法”在测量定位误差和直线度误差时忽略了垂直度误差引起的阿贝误差的影响；“球杆仪法”尽管实现了多轴联动测量，但测量范围仅限以球杆长度为半径的半圆面，并不能完全代表机床的整个工作空间。

2014年德国Etalon AG研制出一种名为LaserTRACER-NG(以下简称LaserTRACER)的测量仪器。该测量仪器主要包括激光头、标靶和电控单元，电控单元与激光头相连接；测量中激光头自动追踪靶标，电控单元自动记录靶标到激光头的实际距离。但目前尚未发现将LaserTRACER用于多项式描述数控机床平动轴几何误差随位置坐标的变化的误差辨识方面的应用。

技术实现要素：

为了解决上述问题，本发明的目的在于提供一种基于LaserTRACER的数控机床平动轴几何误差检测与辨识方法。

为了达到上述目的，基于LaserTRACER的数控机床平动轴几何误差检测与辨识方法包括按顺序进行的下列步骤：

1)构成由数控机床和LaserTRACER组成的测量系统，并利用该测量系统测量得到机床末端位姿误差；

2)建立数控机床21项几何误差和上述机床末端位姿误差之间的映射模型；

3)建立机床末端位姿误差和21项几何误差多项式系数向量之间的映射模型；

4)建立上述多项式系数向量的辨识方程组；

5)对上述多项式系数向量p的辨识方程组进行可辨识性分析；

6)使用Matlab对工作空间中的测量轨迹进行仿真优化。

在步骤1)中所述的测量系统中，数控机床主要包括床身、立柱、X导轨、Y导轨、Y滑台、Z导轨、Z滑台和主轴；其中床身的上端面为工作台，X导轨安装在床身两侧面的X轴方向，门形立柱的下端内侧与X导轨沿X轴方向形成移动副；Y导轨安装在立柱上端横梁上的Y轴方向，Y滑台与Y导轨沿Y轴方向形成移动副；Z导轨安装在Y滑台的Z轴方向，Z滑台与Z导轨沿Z轴方向形成移动副；主轴安装在Z滑台的下端面；LaserTRACER主要包括激光头、标靶和电控单元；标靶安装在主轴的下端面；激光头依次放置在工作台的表面呈口字形的四个位置上，并且与电控单元相连，从而组成数控机床和LaserTRACER的测量系统。

在步骤2)中，所述的建立数控机床21项几何误差和上述机床末端位姿误差之间的映射模型的方法为：首先将数控机床看作由多个刚体串联而成的多体系统；其次使用多体理论描述数控机床上各运动部件之间的拓扑关系；再次使用齐次坐标变换矩阵相乘表示与数控机床相邻部件固连参考坐标系之间的位姿转换关系；最后建立起数控机床21项几何误差与机床末端位姿误差之间的映射模型。

在步骤3)中，所述的建立机床末端位姿误差和21项几何误差多项式系数向量之间的映射模型的方法为：首先将21项几何误差中位置相关的几何误差使用多项式模型描述，位置独立几何误差，即垂直度误差作为一个常数不作处理，得到21项几何误差和21项几何误差多项式系数向量之间的映射关系；其次结合步骤2)中数控机床21项几何误差和机床末端位姿误差之间的映射模型，建立机床末端位姿误差和21项几何误差多项式系数向量之间的映射模型。

在步骤4)中，所述的建立上述多项式系数向量的辨识方程组的方法为：首先在数控机床的工作空间中选定m个测量点，利用步骤3)中的映射模型对于每个测量点得到含3个误差辨识方程的方程组；其次，利用得到的含3个误差辨识方程的m个方程组组合成一个包含3m个误差辨识方程的方程组，即得到上述多项式系数向量的辨识方程组。

在步骤5)中，所述的对上述多项式系数向量p的辨识方程组进行可辨识性分析的方法为：首先，在靶标没有偏置、水平方向和垂直方向偏置三种情况下，观察误差映射矩阵中的列向量，确定其中线性相关以及潜在相关的列向量；其次，将误差映射矩阵中线性相关的列向量以及对应多项式系数向量p中多项式系数向量去掉，而潜在线性相关的列向量通过测量参数设置使得其相互独立；最后，线性独立的多项式系数向量p通过求解联立靶标没有偏置、水平方向和垂直方向偏置情况下的辨识方程组得到。

在步骤6)中，所述的使用Matlab对工作空间中的测量轨迹进行仿真优化的方法为：首先初始给定一组21项几何误差；其次利用步骤2)中机床误差模型计算得到测量点的理想位置误差；再次在上述理想位置误差基础上线性叠加一个高斯噪声用以模拟实际测量结果的随机误差；最后通过最小二乘法计算实际误差值和初始误差的相对误差，多次重复以上过程，直到找到一组测量轨迹使得辨识相对误差足够小，至此，完成使用Matlab对工作空间10中的测量轨迹进行仿真优化的过程。

与现有的辨识方法相比，首先本发明提供的基于LaserTRACER的数控机床平动轴几何误差检测与辨识方法是将激光头放置在数控机床工作台的4个不同位置，分别对安装在数控机床主轴上的标靶的位置进行标定，用类似于“GPS定位”的多边定位原理，能够实现机床误差的快速标定、精密测量，且将数控机床测量范围扩展到数控机床整个工作空间。另外，可以在测量较少数据量的前提下达到较好的辨识效果。其次将辨识结果使用多项式模型拟合位置相关几何误差随机床位置的变化，可以使用建立的误差模型和辨识得到的21项几何误差反向计算数控机床加工空间内任意一点的误差值，为数控机床的加工能力评价以及误差补偿提供数据支持。

附图说明

图1为本发明提供的基于LaserTRACER的数控机床平动轴几何误差检测与辨识方法流程图；

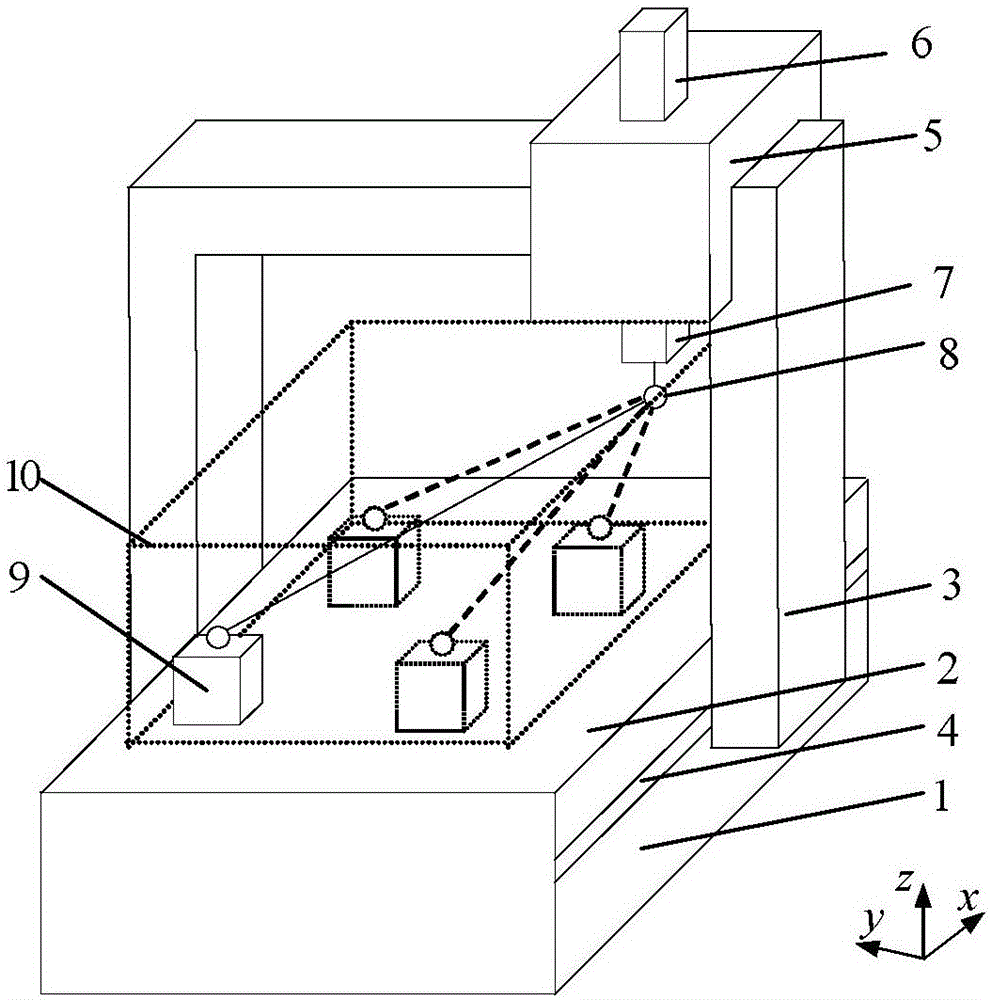
图2为本发明方法采用的测量系统结构示意图。

图3为数控机床结构简图以及坐标系的位置；

图4为测量轨迹仿真流程图；

具体实施方式

下面结合附图和实施例，对本发明作进一步详细说明。

如图1所示，本发明提供的基于LaserTRACER的数控机床平动轴几何误差检测与辨识方法包括按顺序进行的下列步骤：

1)构成由数控机床和LaserTRACER组成的测量系统，并利用该测量系统测量得到机床末端位姿误差；

如图2所示，在所述的测量系统中，数控机床主要包括床身1、立柱3、X导轨4、Y导轨、Y滑台5、Z导轨、Z滑台6和主轴7；其中床身1的上端面为工作台2，X导轨4安装在床身1两侧面的X轴(前后)方向，门形立柱3的下端内侧与X导轨4沿X轴方向形成移动副；图中未示出的Y导轨安装在立柱3上端横梁上的Y轴(左右)方向，Y滑台5与Y导轨沿Y轴方向形成移动副；图中未示出的Z导轨安装在Y滑台5的Z轴(上下)方向，Z滑台6与Z导轨沿Z轴方向形成移动副；主轴7安装在Z滑台6的下端面；LaserTRACER主要包括激光头9、标靶8和图中未示出的电控单元；标靶8安装在主轴7的下端面；激光头9依次放置在工作台2的表面呈口字形的四个位置上，并且与电控单元相连；标靶8能够随主轴7在X、Y、Z轴方向移动的最大范围所围成的空间称为工作空间10；在测量过程中，四个激光头9自动追踪装夹在主轴7下端面的靶标8，主轴7在工作空间10内移动到某一位置时，电控单元自动记录靶标8到相应激光头9间的实际距离，并将该位置作为一个测量点，然后减去靶标8到相应激光头9间的理想位置，即得到数控机床刀具与工件相对位姿误差(以下简称机床末端位姿误差)。LaserTRACER需要测量机床工作空间10中若干个点位才可以准确标定数控机床的几何误差，而这些测量点位依次连接构成数控机床的误差测量轨迹。

2)建立数控机床21项几何误差和上述机床末端位姿误差之间的映射模型；

数控机床的几何误差，根据是否和当前数控机床运动位置相关，可分为位置相关几何误差(PDGEs)和位置独立几何误差(PIGEs)。如图3所示，本发明以一台精密卧式加工中心为例，对本发明的辨识方法加以说明，上述加工中心在仅考虑平动轴几何误差的情况下共有21项几何误差：与三个轴线坐标位置相关的9项位置误差和9项转角误差，以及位置独立的三个轴线之间的3项垂直度误差，共计18项PDGEs、3项PIGEs，如表1所示。

表1数控机床的21项几何误差

表中δ_x、δ_y、δ_z代表位置误差，角标表示误差的方向；ε_x、ε_y、ε_z代表转角误差，角标表示转角误差旋转轴线的方向，括号中的x、y、z表示X、Y、Z轴的运动位置坐标；例如δ_i(j),其中i,j＝x,y,z表示在坐标轴j运动位置坐标为j时，沿坐标轴i方向的位置误差，ε_i(j),其中i,j＝x,y,z表示在坐标轴j运动位置坐标为j时，绕坐标轴i旋转的转角误差；ε_xy、ε_yz、ε_xz分别表示坐标轴X与Y、Y与Z、X与Z之间的垂直度误差。

数控机床是一种由多个刚体串联而成的多体系统，可使用多体理论描述数控机床上各运动部件之间的拓扑关系，用齐次坐标变换矩阵相乘表示与数控机床相邻部件固连参考坐标系之间的位姿转换关系，从而建立起数控机床21项几何误差与机床末端位姿误差之间的映射模型(以下简称机床误差模型)：

其中，为机床末端位姿误差向量，为由数控机床21项几何误差构成的向量，A_r为机床末端位姿误差和21项几何误差之间的映射矩阵。

为了书写方便，将式(1)拆分成如下形式：

式(2)中位置相关的几何误差向量为：

位置独立的几何误差向量为：

式(2)中A_rx、A_ry、A_rz分别为与x、y、z轴相关的各项误差的误差映射矩阵，A_rs为与垂直度误差相关的误差映射矩阵；为与x、y、z轴位置相关的几何误差向量、为垂直度误差向量，其为常数。

3)建立机床末端位姿误差和21项几何误差多项式系数向量之间的映射模型；

将上述位置相关的几何误差向量用多项式模型描述；位置独立几何误差，即垂直度误差为一个常数，故不作处理。

LaserTRACER的测量方式为相对误差测量，因而定义数控机床的工作台2的参考坐标系的坐标原点处各项位置相关几何误差数值为零，即多项式常数项为零。

位置误差(包括定位误差与直线度误差)为：

转角误差(包括俯仰角、偏摆角、滚转角误差)为：

式(5)、(6)中δ_ij,k表示位置误差δ_i(j)的多项式模型中第k个多项式系数；ε_ij,k表示转角误差ε_i(j)的多项式模型中第k个多项式系数；k为n阶多项式中的k次幂项。

在式(5)、(6)中：

式中分别为描述位置误差δ_i(j)、转角误差ε_i(j)的系数向量，为对应的坐标位置矩阵；j为X轴或Y轴或Z轴的当前坐标位置。当靶标8的位置坐标(x,y,z)已知时，坐标位置矩阵为已知量。

将式(5)、(6)代入与X轴位置相关的几何误差向量中有：

同理可以得到：

和

将式(8)代入式(2)可以得到21项几何误差与其对应的多项式系数向量之间的关系：

将式(9)代入式(1)得到机床末端位姿误差和21项几何误差多项式系数向量之间的关系：

在式(10)中，为工作空间10中某一点处机床末端位姿误差向量，p为21项几何误差多项式系数向量(以下简称多项式系数向量)。

4)建立上述多项式系数向量的辨识方程组；

上述式(10)中，使用LaserTRACER测量得到工作空间10中某一点处机床末端位姿误差向量中含有3个误差分量，可以组成含有3个误差辨识方程的方程组，而多项式系数向量p中共有18n+3个未知系数，方程组无法求解，增加工作空间10中测量的点数，使得方程的数量大于等于未知系数的数量即可求解。假设在工作空间10中一共测量m个测量点，对于第i个测量点，(i＝1,2,…,m)，考虑到有m个测量点，则多项式系数向量p的辨识方程组为：

在式(11)中，n为用以描述位置相关的几何误差多项式的阶数；m为使用LaserTRACER在工作空间10中测量的测量点总数；为在第i个测量点测得的机床末端位姿误差向量；p为多项式系数向量，包括位置相关几何误差的18n项多项式系数向量和位置独立的3项垂直度多项式系数向量；M_i为第i个空间网格点对应的误差映射矩阵，包含精密机床结构参数、机床运动位置信息。

理论上，当3m≥18n+3时，即方程个数大于等于未知数个数，可以辨识出多项式系数向量p。

5)对上述多项式系数向量p的辨识方程组进行可辨识性分析；

将上述误差映射矩阵M_i拆分成如下形式：

M_i＝[M_xi M_yi M_zi M_si] (12)

式中M_xi、M_yi、M_zi、M_si分别为与数控机床三个坐标轴x、y、z和垂直度误差相关的误差映射矩阵，多项式系数向量p可辨识的核心条件为误差映射矩阵M_i中的列向量均相互独立；

(1)观察误差映射矩阵M_xi、M_yi、M_zi、M_si，当靶标8的位置没有偏置时，即靶标8坐标向量(表示安装在主轴7上的标靶8的几何中心O_T在主轴坐标系T-xyz中的位置向量)，误差映射矩阵M_i中有五对列向量，即转角误差ε_y(x)、ε_x(y)、ε_y(y)、ε_z(y)与位置误差δ_y(x)、δ_x(y)、δ_y(y)、δ_z(y)以及位置误差δ_y(y)中的一次项与垂直度误差ε_xy分别线性相关，与它们相对应的多项式系数向量p中的多项式系数无法辨识。

(2)转角误差ε_z(y)对应的误差映射矩阵M_y中列向量有三种情况：

A.靶标8没有偏置时为零向量，和误差映射矩阵中所有列向量相关。

B.靶标8在x方向偏置时，和位置误差δ_y(y)对应的误差映射矩阵的列向量相关。

C.靶标8在y方向偏置时，和位置误差δ_x(y)对应的误差映射矩阵的列向量相关。

(3)除了上面提到的5对列向量之外，还有3对列向量需要特别注意，他们分别是：误差映射矩阵M_xi、M_yi、M_zi中的前三列，即第1列位置误差δ_x(x)、δ_x(y)和δ_x(z)可能线性相关，第2列位置误差δ_y(x)、δ_y(y)和δ_y(z)可能线性相关，第3列位置误差δ_z(x)、δ_z(y)和δ_z(z)可能线性相关。为了使上述3对列向量相互独立，令在数控机床的工作空间10中展开测量的起始点的三个坐标值互不相等，即x≠y≠z。

误差映射矩阵M_i中线性相关的列向量，使得上述线性相关的多项式系数向量p无法辨识，故应去掉多项式系数向量p中这5对多项式系数向量以及与其相对应的误差映射矩阵M_i中相应的列向量，此时可将线性独立的14n+3项多项式系数向量p辨识出来。而对剩余的4n项线性相关的多项式系数向量p，通过靶标8的水平和垂直偏置后，重复测量与上述相同的m个测量点的末端位姿误差，将得到的多项式系数向量p的辨识方程组和上述靶标8没有偏置时得到多项式系数向量p的辨识方程组联立，求解上述联立后的辨识方程组即可辨识。

6)使用Matlab对工作空间中的测量轨迹进行仿真优化；

经过上述处理，多项式系数向量p中共含有14n+3项多项式系数，因而只要在测量轨迹上均匀选取3m≥14n+3个测量点位，使得误差映射矩阵M满秩，即可辨识出多项式系数向量p中所有多项式系数。而为了使得误差辨识精度更高，则需要对工作空间10中m个测量点的空间位置分布，也即测量轨迹使用Matlab进行仿真优化，使得测量轨迹同时满足以下3个条件：

(1)所选择的m个测量点连接而成的测量轨迹遍历数控机床所有可控自由度，并均匀分布在数控机床的整个工作空间10中。

(2)使用LaserTRACER测量机床末端位置位姿误差时，主轴7所走过的测量轨迹线足够少，以减少误差的测量时间。

(3)使得步骤4)、5)中得到的多项式系数向量p的辨识方程组的误差辨识精度小于2微米。

使用Matlab对测量轨迹进行仿真优化，仿真流程参见图4。首先初始给定一组21项几何误差，利用机床误差模型计算得到测量点的理想位置误差，在上述理想位置误差基础上线性叠加一个高斯噪声用以模拟实际测量结果的随机误差，而后通过最小二乘法计算实际误差值和初始误差的相对误差。

第1步：设定工作空间10内测量轨迹组成的测量空间的两个对角点在机床坐标系中的坐标值、测量轨迹线组合方案、靶标8的安装位置坐标向量、用于拟合位置相关几何误差的多项式的阶数n以及每条测量轨迹线上均匀分布的测量点个数m；

第2步：初始给定一组多项式系数向量用于仿真(记为)；

第3步：使用数控机床的误差模型也即式(10)，计算得到测量轨迹线上测点对应的初始机床末端位姿误差向量

第4步：在初始机床末端位姿误差向量上叠加均值为零，标准差为σ正态分布N(0,σ)的扰动误差，以模拟测量噪声及其它不确定因素，得到实际机床末端位姿误差向量

第5步：计算误差映射矩阵M的条件数和秩，使用最小二乘法计算得到实际多项式系数和相对误差ε；

第6步：评价测量轨迹，当误差映射矩阵M满秩且条件数较小，且相对误差足够小的时候，测量轨迹仿真优化结束。

多次重复以上过程，直到找到一组最优化测量轨迹使得辨识相对误差足够小。至此，基于LaserTRACER的数控机床平动轴几何误差检测与辨识算法介绍完毕，可以使用此算法测量并辨识得到21项几何误差，为数控机床的加工能力评价以及误差补偿提供数据支持。

尽管上面结合附图对本发明的优选实施例进行了描述，但是本发明并不局限于上述的具体实施方式，上述的具体实施方式仅仅是示意性的，并不是限制性的，本领域的普通技术人员在本发明的启示下，在不脱离本发明宗旨和权利要求所保护的范围情况下，还可以作出很多形式，这些均属于本发明的保护范围之内。