一种非球面在位检测中的位置误差标定方法与流程

本发明属于精密测试位置标定技术领域，具体涉及一种非球面在位检测中的位置标定方法。

背景技术：

非球面镜片主要应用于光学成像，激光武器，核聚变等场合，由于大口径非球面体积大，质量高，采用离线手段进行测量在工件搬运方面非常困难，并且在进行二次装卡时测量坐标系和工件坐标系之间会产生较大的误差，所以采用在线/在位测量是必不可少的。又因为测量工作对外界环境要求很高，所以一般都在恒温间中通过专用的测量设备完成，因而大口径非球面在位测量的技术一直是一个难点。

传统的非球面测量路径有如下两种：子午线式路径规划和圆周式路径规划，子午线式路径规划是对非球面的母线进行测量，即要求每条测量路径都通过非球面中心；而圆周式路径规划则是以非球面中心为基准，沿着x方向每隔一段距离，转台旋转一周进行测量。可以看出，无论是采用哪种路径进行非球面面型检测，中点位置的寻找都是至关重要的。

相比于离线测量系统，目前的在位系统都较为简单，默认转台中心和工件中心完全重合，而在实际情况中，由于外界振动和转台径向跳动的影响，会使两者具有一定的偏移,并且由于位移传感器的装卡问题，测量坐标系和转台坐标系也无法完全重合。这两种误差在后续的测量过程中，特别是对工件面型要求较高时就会导致较大的误差，从而影响测量精度。

技术实现要素：

为了克服上述现有技术的缺点，本发明的目的在于提供一种非球面在位检测中的位置标定方法，其在测量中同时消除转台中心和工件中心的误差，以及位移传感器的装卡误差，从而获得更加的测量精度。

为了达到上述目的，本发明采取的技术方案为：

一种非球面在位检测中的位置标定方法，包括以下步骤：

1)首先采用三点法进行转台中心标定：

1.1)将标准球置于转台任意位置，利用位移传感器测量标准球表面上n点的坐标，n≥4，根据坐标拟合出标准球球心坐标所在位置；

1.2)在保证标准球和转台相对位置不发生改变的情况下，转动转台m次，m≥2，分别对标准球表面上n点进行测量，拟合出在m个位置时的标准球球心位置；

1.3)通过步骤1.1)和1.2)所拟合出的标准球球心坐标，拟合出转台中心坐标；

2)以转台中心为基准，进行非球面中心四点标定：

2.1)以步骤1.3)中拟合出的转台中心作为非球面中心的初始位置(0,0)，在该点处所测得的工件表面的Z坐标为0，即认为此点为工件中心；

2.2)分别测量(0，d)、(d，0)、(0，-d)、(-d，0)点处工件表面的Z坐标，记做Z_(0,d)，Z_(d,0)，Z_(0,-d)和Z_(-d,0)；

2.3)将点Z_(0,d)带入非球面方程中，

R——非球面顶点曲率半径；

K——非球面系数；

把x设为0，计算出y的值，记做Y_Z(0,d)；同理，带入Z_(d,0)，Z_(0,-d)和Z_(-d,0)的值，在带入Z_(d,0)，和Z_(-d,0)时将y设0计算x，计算出X_Z(d,0)，-|Y_Z(0,-d)|和-|X_Z(-d,0)|，并以(X_Z(d,0)-|X_Z(-d,0)|，Y_Z(0,d)-|Y_Z(0,-d)|，)为新的工件中心进行迭代计算，直到前一次和后一次所计算出来的工件中心位置之差小于ε，就认为该点位置为实际的工件中心；

其中，设测量精度要求为k，非球面口径为φ，则ε根据式(2)算出，

3)测量非球面的面型数据，通过对测量数据进行处理，计算出标定的残余误差并对测量结果进行优化：

3.1)转台中心标定误差：

分析步骤1.3)中转台中心拟合的残余误差在非球面检测中所造成的影响：在转台坐标系中，真实的转台中心坐标为(0,0)，而经过步骤1.3)拟合之后的转台中心为(m，n)，那么采用子午线测量法，在非球面测量中，因为转台中心而导致的误差为：

e_lo＝f(r×cos(θ+180°),r×sin(θ+180°))-f(ρ×cos(θ+180°-γ),ρ×sin(θ+180°+γ)) (3)

其中：

γ＝arcsin(n/ρ)；

3.2)工件中心与转台中心的偏差分析:

分析步骤2.3)中工件中心标定的误差所造成的影响，非球面方程简化为

z'＝f(x',y') (4)

理论上工件中心为(x_o',y₀')，但是实际上，经过标定出来的转台中心为(x',y')，所以工件中心标定的误差为：

e_wc＝f(x',y')-f(x-x₀',y-y₀') (5)

3.3)非球面半径R的误差：

非球面顶点曲率半径R的加工误差也会对测量结果的评价产生影响，所以实际的曲率半径R应为R+ΔR；

3.4)接下来进行计算，设非球面镜中心的坐标为(x_o,y₀,z₀)，而所标定出的转台中心距离实际转台中心的距离为(m,n)，非球面的实际顶点曲率半径为R+ΔR,原始测量数据为(x_i',y_i',z_i')，

考虑到标定出的转台中心与实际转台中心之间的误差，带入测量数据并将其分解到X，Y，Z三个方向，得到处理后的数据(x_i”,y_i”,z_i”)：

再带入非球面中心真实坐标，得到：

接下来加入非球面曲率半径误差，得到：

z_i-f(x_i,y_i,ΔR)＝0 (8)

其中

式(9)中，c＝1/(R+ΔR)；

但是参数是未知的，所以在实际应用中，用使上式偏差最小的参数来代替,

要使上式最小，则要使其各项参数的一阶偏导数为零，所以对其求偏导，之后将测量数据带入求偏导之后的方程

采用牛顿法对其进行求解就精确的求出上述各项误差，从而提高测量精度。

本发明的有益效果为：利用位移传感器对非球面进行检测，通过对标准球和非球面表面的测量和计算，完成了非球面在位测量中传感器的位置标定和非球面位姿误差的定量分析，从而实现测量坐标系，工件坐标系，转台坐标系之间的统一，减小了测量误差。并且除标准球外不需要使用任何额外的设备，系统简单，易于实现。

附图说明

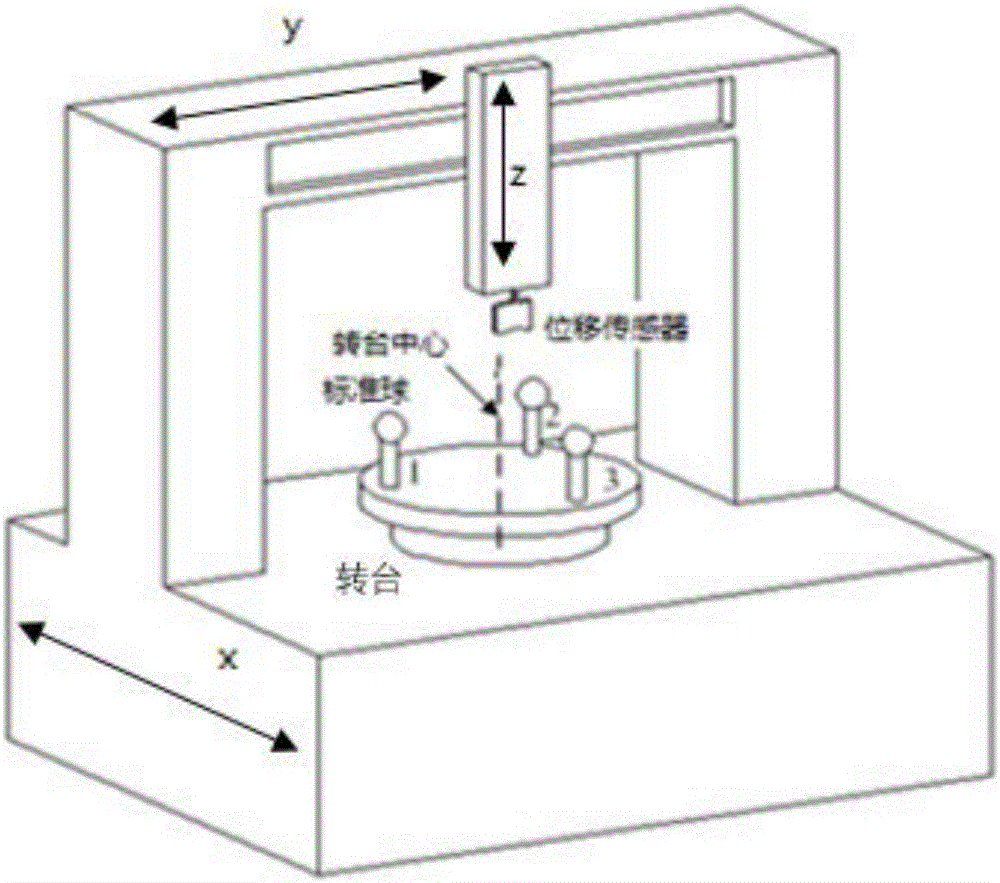
图1为转台中心标定示意图。

图2为标准球表面采点路径规划示意图。

图3为标准球球心拟合转台中心示意图。

图4为四点定心原理图。

图5为四点定心流程图。

图6为转台中心标定误差示意图。

具体实施方式

下面结合附图对本发明作详细描述。

一种非球面在位检测中的位置标定方法，包括以下步骤：

1)首先采用三点法进行转台中心标定：

1.1)参照图1，转台中心标定系统由位移传感器和标准球组成，传感器安装在三坐标机床的Z轴上，方向与z轴负方向一致，将标准球置于转台上任意位置，记为位置1，已知标准球方程为

(x-x₀)²+(y-y₀)²+(z-z₀)²＝R² (12)

球心坐标为(x₀,y₀,z₀),所以理论上测得球面上4点就能够通过式(2)拟合出标准球球心的坐标；

但是由于测量存在误差，所以需要测量大量数据来进行标准球球心坐标拟合，具体过程为：先进行标准球表面采点路径规划，参照图2，传感器在标准球表面按照1→2→…→9→2的路径进行移动，其中在每段上均匀采集10个点，之后对这些点采用最小二乘法进行球心拟合；

1.2)在保证标准球和转台相对位置不发生改变的情况下，转动转台m次(m≥2)，同样通过步骤1.1)的方法拟合出标准球球心坐标；

1.3)通过步骤1.1)和1.2)所拟合出的标准球球心坐标，采用最小二乘法拟合出转台中心坐标，原理如图3所示；

2)以转台中心为基准，进行非球面中心四点标定，理论上在在位测量中非球面工件的中心和转台中心应该完全重合，但是由于加工中转台径向跳动和外界震动的干扰，会使非球面中心和转台中心产生偏差，即在以转台中心为原点，对非球面进行测量时，测量路径无法与母线重合，这样在评价中就会带入误差，故采用四点定心的方法来对非球面中心进行标定，如图4、图5所示；

2.1)以步骤1.3)中拟合出的转台中心作为非球面中心的初始位置(0,0)，在该点处所测得的工件表面的Z坐标为0，即认为此点为工件中心；

2.2)分别测量(0，d)、(d，0)、(0，-d)、(-d，0)点处工件表面的Z坐标，因为在加工中转台径向跳动和外界振动的干扰，4点的Z坐标会有所区别，把这四点的Z坐标记做Z_(0,d)，Z_(d,0)，Z_(0,-d)和Z_(-d,0)；

2.3)将点Z_(0,d)带入非球面方程中，

R——非球面顶点曲率半径；

K——非球面系数；

把x设为0，计算出y的值，记做Y_Z(0,d)；同理，带入Z_(d,0)，Z_(0,-d)和Z_(-d,0)的值，在带入Z_(d,0)，和Z_(-d,0)时将y设0计算x，计算出X_Z(d,0)，-|Y_Z(0,-d)|和-|X_Z(-d,0)|，并以(X_Z(d,0)-|X_Z(-d,0)|，Y_Z(0,d)-|Y_Z(0,-d)|，)为新的工件中心进行迭代计算，直到前一次和后一次所计算出来的工件中心位置之差小于ε，就认为该点位置为实际的工件中心；

其中，设测量精度要求为k，非球面口径为φ，则ε根据式(2)算出，

3)测量非球面的面型数据，通过对测量数据进行处理，计算出标定的残余误差并对测量结果进行优化，理论上一个工件在空间中的摆放位置有6项自由度，但由于转台在运行中C轴一般较为平稳，不会产生偏摆，所以工件所产生的倾斜很小，误差可以被忽略，所以别针对工件和转台中心的偏差，传感器和工件中心的偏差，以及非球面曲率半径误差进行分析，

3.1)转台中心标定误差：

由于传感器误差和标准球面型精度的影响，在步骤1)中采用标准球标定出来的转台中心必然会有一定的偏差，如图6所示,

设实际的转台中心为(0,0)，而由于在测量坐标系中转台位置是通过拟合而来，存在一定误差，所以认为所标定出的转台中心相对于实际转台中心的位置为(m,n),因为采用子午线式测量，每次沿x方向测量一条母线然后转过θ角度再进行下一次测量,理论上在测头移动到-r点时测得的应该就是(r×cos(θ+180°),r×sin(θ+180°))点处的坐标，但是当存在误差(m,n)时，所测量的坐标点为(ρ×cos(θ+180°-γ),ρ×sin(θ+180°+γ))

其中：

γ＝arcsin(n/ρ)

所以，由于传感器标定不对中所造成的误差为

e_lo＝f(r×cos(θ+180°),r×sin(θ+180°))-f(ρ×cos(θ+180°-γ),ρ×sin(θ+180°+γ)) (3)

3.2)工件中心与转台中心的偏差分析:

非球面方程可以简化为

z'＝f(x',y') (4)

理论上，转台中心的坐标为(x_o',y₀')，且在在位测量系统中，工件中心应与转台中心重合，但是实际上，由于转台径向跳动和外界振动的影响，两者之间会存在一定的偏差，(x，y)为测量点的横纵坐标，所以因为转台和非球面的中心偏差导致的误差为：

e_wc＝f(x',y')-f(x-x₀',y-y₀') (5)

3.3)非球面半径R的误差：

非球面顶点曲率半径R的加工误差也会对测量结果的评价产生影响，所以设实际的曲率半径R为R+ΔR；

3.4)接下来进行计算，设非球面镜中心的坐标为(x_o,y₀,z₀)，而所标定出的转台中心距离实际转台中心的距离为(m,n)，非球面的实际顶点曲率半径为R+ΔR,原始测量数据为(x_i',y_i',z_i')，

以二次非球面为例，高次非球面同理可得，考虑到标定出的转台中心与实际转台中心之间的误差，带入测量数据并将其分解到X，Y，Z三个方向，得到处理后的数据(x_i”,y_i”,z_i”)：

再带入非球面中心真实坐标，得到：

接下来加入非球面曲率半径误差，得到：

z_i-f(x_i,y_i,ΔR)＝0 (8)

其中

式(11)中，c＝1/(R+ΔR)；

但是参数是未知的，所以在实际应用中，用使式(9)最小的参数来代替,

要使式(10)最小，则要使其各项参数的一阶偏导数为零，所以先对式(10)求偏导，之后将测量数据带入式(11)：

最后在matlab中对方程组采用牛顿法进行求解，就能计算出上述的所有误差，从而对测量结果进行优化。