一种基于随机集理论的多雷达异步数据分布式融合方法与流程

本发明属于雷达技术领域，涉及随机集理论下的多目标跟踪、异步雷达数据处理和多传感器融合技术研究。

背景技术：

信息化条件下，组网雷达充分发挥单部雷达的作用，把不同体质、不同频段、不同工作模式的雷达适当部署，通过通信数据链构成一个网络，并由一个中心基站进行调控，借助于信息融合技术将各部雷达接收到的信息进行处理进而得到可信度高的雷达情报。

传统的数据融合之前都需要进行多源数据关联，如最近邻数据关联(NNDA)、概率数据关联(PDA)、联合概率数据关联(JPDA)、简易联合概率数据关联(CJPDA)和最近邻联合概率数据关联(NNJPDA)等。这些方法都是利用雷达获取与目标状态向量直接相关的信息来进行多目标关联，采用经典推理和统计方法、贝叶斯推理技术、Dempster-Shafer技术和聚类分析等技术实现融合过程，但是当目标数目较多且虚警概率较大时，其计算量非常大且易出错，造成后续的融合结果很差。针对这一缺点，Mahler在研究多目标贝叶斯滤波问题时提出随机集理论，他利用一阶统计矩近似方法对多目标后验概率密度函数求集合积分运算得到多目标强度，避免了直接计算完全后验概率密度函数，避免了数据关联过程，同时该算法还可以实时地对目标个数进行评估，适用于目标个数未知且时变的场景。随着随机集的发展，学者们相继将随机集理论应用到融合领域。2013年，在文献“Distributed Fusion of PHD Filters Via Exponential Mixture Densities[J].IEEE Journal of Selected Topics in Signal Processing,2013,7(3):521-531.”中，将PHD应用到分布式融合理论中，在利用PHD跟踪目标之后，采用协方差交叉方法进行数据的融合处理，但是仅仅是针对数据同步的场景。但是在实际雷达场景中，由于开机时间、扫描周期不同等，导致雷达之间接收到的数据是异步的，因此该模型只能在雷达接收的数据是同步的场景中，不能应用于实际雷达场景中。

技术实现要素：

本发明的目的是针对背景技术存在的缺陷，研究设计了一种针对多雷达异步数据传输下的基于随机集理论分布式融合算法，解决现有利用传统融合跟踪技术来解决异步数据处理的问题。

本发明的解决方案是采用分布式融合跟踪处理的方式，首先对每部雷达的PHD跟踪采用混合高斯模型(Gaussian-Mixture)来表示，在融合之前设定好融合节点，然后分别将各部雷达在融合区间内的接收到的最新的PHD通过Kalman预测的方法外推至融合节点时刻，最后将在融合节点时刻的所有概率假设密度通过广义协方差交叉算法进行融合处理，得到融合数据。该方法有效解决了在实际应用中数据异步且计算量大的问题，从而实现任意部雷达进行目标跟踪时异步数据的处理问题。

本发明提出了一种基于随机集理论的多雷达异步数据序贯式融合方法，具体包括步骤：

步骤1：对高斯混合概率假设密度进行参数化表征；

其中，v_k-1(x)表示在k-1时刻时的多目标后验概率强度，x表示目标状态集合；J_k-1表示在k-1时刻的高斯分量的个数；表示在k-1时刻第i个高斯分量的权重；表示在k-1时刻期望为方差为的第i个高斯分量对应的高斯密度函数，且满足

步骤2：建立模型，得到预测的多模型的高斯混合概率密度假设强度；

2.1对幸存目标进行预测：

其中，v_S,k|k-1(x)表示在k时刻幸存目标S的强度；p_S,k表示k时刻目标S的幸存概率；是幸存目标在k时刻的第i个高斯分量的期望，且满足：是幸存目标在k时刻的第i个高斯分量的方差，且满足：其中F_k-1表示k-1时刻的状态转移矩阵，Q_k-1表示k-1时刻的过程噪声协方差矩阵；

2.2对衍生目标进行预测：

其中，v_β,k|k-1(x)表示在k-1时刻存在的目标在k时刻衍生出状态为x的目标(衍生目标)的强度，J_β,k表示在k时刻衍生目标高斯分量的个数；是k-1时刻第i个高斯分量的权重；是k时刻衍生的第l个高斯分量的权重；是幸存目标在k时刻的第i个高斯分量衍生出的第j个高斯分量的期望，且满足：是幸存目标在k时刻的第i个高斯分量衍生出的第j个高斯分量的方差，且满足：

2.3对新生目标进行预测：

其中，γ_k(x)表示在k时刻时的新生目标后验概率强度；J_γ,k表示新生目标在k时刻的高斯分量的个数；表示在k时刻第i个高斯分量的权重；表示期望为方差为的第i个高斯分量对应的高斯密度函数；

步骤3：对多部雷达接收到的数据根据时间序列采用如下公式进行依次更新：

其中：

其中，分别表示k时刻第N次更新后和预测后的强度函数；和分别表示k时刻第N次预测时的幸存强度函数、衍生强度函数和新生强度函数；N表示雷达总数；表示k时刻第N次预测后的强度函数；p_D,k表示雷达检测概率；表示时刻第i部雷达的量测集合；J_k|k-1表示k时刻预测状态对应的高斯分量的个数；和分别表示k时刻利用第i部雷达的量测更新后第j个高斯分量的权重、均值和方差；和分别表示表示k时刻利用第i部雷达的第j个高斯分量的权重、均值和方差；κ_k(z)表示k时刻的杂波密度，H_k表示k时刻的状态转移矩阵，R_k表示k时刻的量测噪声协方差矩阵；

步骤4：高斯分量的剪枝处理；

T是设定的门限；

剪枝循环开始：

I:＝I\L

直到时结束剪枝循环处理；

其中，L是满足门限的高斯分量集合；是剪枝前的高斯分量的权重、均值和方差；和是剪枝后的高斯分量的权重、均值和方差；

步骤5：目标个数和状态提取；

剪枝处理后的高斯分量，满足权重值大于0.5的高斯分量即是目标状态。

本发明提出了另一种基于随机集理论的多雷达异步数据分布式融合方法，具体包括步骤：

步骤1：对高斯混合概率假设密度进行参数化表征；

其中，v_k-1(x)表示在k-1时刻时的多目标后验概率强度，x表示目标状态集合；J_k-1表示在k-1时刻的高斯分量的个数；表示在k-1时刻第i个高斯分量的权重；表示在k-1时刻期望为方差为的第i个高斯分量对应的高斯密度函数，且满足

步骤2：建立模型，得到预测的多模型的高斯混合概率密度假设强度；

2.1对幸存目标进行预测：

其中，v_S,k|k-1(x)表示在k时刻幸存目标S的强度；p_S,k表示k时刻目标S的幸存概率；是幸存目标在k时刻的第i个高斯分量的期望，且满足：其中F_k-1表示状态转移矩阵；是幸存目标在k时刻的第i个高斯分量的方差，且满足：其中Q_k-1表示过程噪声协方差矩阵；

2.2对衍生目标进行预测：

其中，v_β,k|k-1(x)表示在k-1时刻存在的目标在k时刻衍生出状态为x的目标(衍生目标)的强度，J_β,k表示衍生目标在k时刻高斯分量的个数；是k-1时刻第i个高斯分量的权重；是k时刻衍生的第l个高斯分量的权重；是幸存目标在k时刻的第i个高斯分量衍生出的第j个高斯分量的期望，且满足：是幸存目标在k时刻的第i个高斯分量衍生出的第j个高斯分量的方差，且满足：

2.3对新生目标进行预测：

其中，γ_k(x)表示在k时刻时的新生目标后验概率强度；J_γ,k表示新生目标在k时刻的高斯分量的个数；表示在k时刻第i个高斯分量的权重；表示期望为方差为的第i个高斯分量对应的高斯密度函数；

步骤3：进行目标状态的更新：

对于第i部雷达：

其中，分别表示第i部雷达在第k时刻更新后和预测后的状态；和分别表示k时刻第N次预测时的幸存强度函数、衍生强度函数和新生强度函数；表示时刻第i部雷达的量测集合；p_D,k表示雷达检测概率；J_k|k-1表示k时刻预测状态对应的高斯分量的个数；和分别表示k时刻利用第i部雷达的量测更新后第j个高斯分量的权重、均值和方差；κ_k(z)表示k时刻的杂波密度；表示量测为z时对应的高斯函数的值；

步骤4：得到多部雷达的距离融合节点最近的局部后验密度之后，采用广义协方差交叉算法进行融合处理，得到融合结果：

其中：

其中，s_k(x)表示融合后的强度函数；N_a和N_b分别是雷达a和b的高斯分量在第k个融合节点的个数；ω表示雷达a的权重；和分别表示雷达a和b距第k个融合节点最近的局部后验密度的过程噪声协方差矩阵；F_a,k、和F_b,k、分别表示雷达a和b距第k个融合节点最近的局部后验密度的状态转移矩阵及其转置；和分别表示融合前雷达a和雷达b的均值和协方差；和分别表示雷达a距第k个融合节点最近的局部后验密度预测后的权重、均值和方差；和分别表示雷达b距第k个融合节点最近的局部后验密度预测后的权重、均值和方差；和分别表示雷达a和b在第k个融合节点的融合后的权重、均值和方差；

步骤5：高斯分量的剪枝处理；

T是设定的门限；

剪枝循环开始：

I:＝I\L

直到时结束剪枝循环处理；

其中，L是满足门限的高斯分量集合；是剪枝前的高斯分量的权重、均值和方差；和是剪枝后的高斯分量的权重、均值和方差；

步骤6：目标个数和状态提取；

剪枝处理后的高斯分量，满足权重值大于0.5的高斯分量即是目标状态。

通过上面的步骤，就可以得到基于随机集理论下的异步数据处理过程，实现对机动多目标的跟踪及运动模型的估计。

本发明的创新点在于针对异步数据处理时，结合随机集理论提出了两种数据处理方式，序贯式融合处理和固定节点融合处理。序贯式融合方法处理利用的原始数据信息较多，误差较小，但是计算量较大；而固定节点融合处理方法是在各部雷达分别进行跟踪处理的同时，在设定好的固定融合节点处进行广义协方差交叉融合，其融合精度高，且所需计算量较小。

附图说明

图1是本发明提供的序贯式融合流程图。

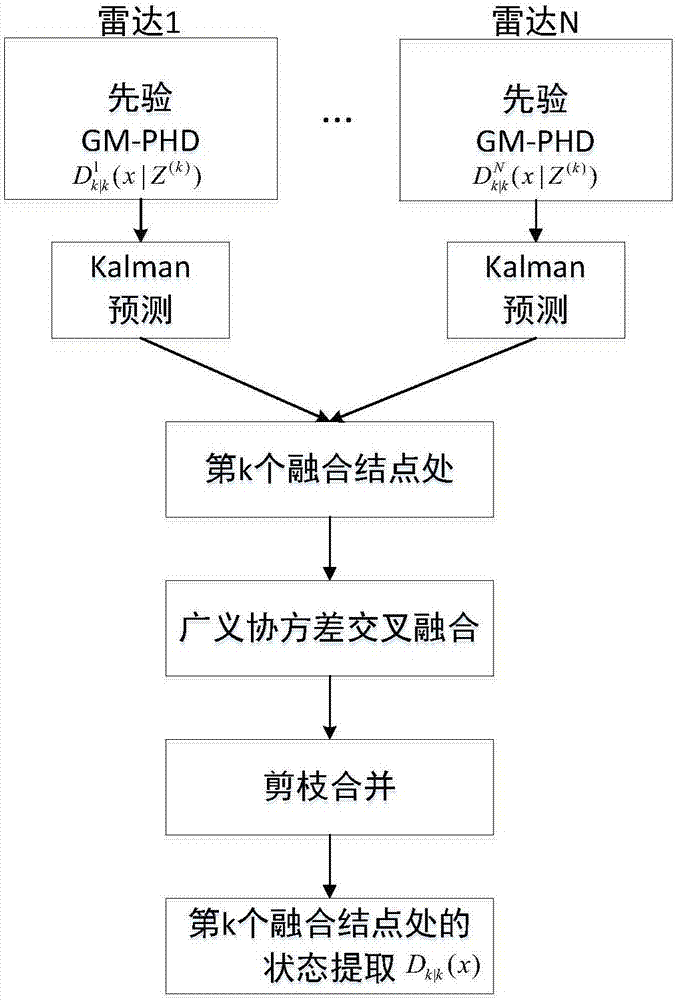
图2是本发明提供的固定节点融合流程图。

图3是本发明提供序贯式融合的示意图。

图4是本发明提供固定节点融合的示意图。

图5是基于序贯式融合的跟踪目标个数。

图6是基于固定节点融合的跟踪目标个数。

图7是基于序贯式融合和固定节点融合处理的跟踪目标误差效果。

具体实施方式

本发明主要采用仿真实验的方法进行验证，所有步骤、结论都在Matlab2015b上验证正确。下面就具体实施方式对本发明作进一步的详细描述。

步骤1：对高斯混合概率假设密度进行参数化表征；

其中，v_k-1(x)表示在k-1时刻时的多目标后验概率强度，x表示目标状态集合；J_k-1表示在k-1时刻的高斯分量的个数；表示在k-1时刻第i个高斯分量的权重；表示在k-1时刻期望为方差为的第i个高斯分量对应的高斯密度函数，且满足

步骤2：建立模型，得到预测的多模型的高斯混合概率密度假设强度；

2.1对幸存目标进行预测：

其中，v_S,k|k-1(x)表示在k时刻幸存目标S的强度；p_S,k表示k时刻目标S的幸存概率；是幸存目标在k时刻的第i个高斯分量的期望，且满足：是幸存目标在k时刻的第i个高斯分量的方差，且满足：其中F_k-1表示k-1时刻的状态转移矩阵；Q_k-1表示k-1时刻的过程噪声协方差矩阵。

2.2对衍生目标进行预测：

其中，v_β,k|k-1(x)表示在k-1时刻存在的目标在k时刻衍生出状态为x的目标(衍生目标)的强度，J_β,k表示衍生目标在k时刻高斯分量的个数；是k-1时刻第i个高斯分量的权重；是k时刻衍生的第l个高斯分量的权重；是幸存目标在k时刻的第i个高斯分量衍生出的第j个高斯分量的期望，且满足：是幸存目标在k时刻的第i个高斯分量衍生出的第j个高斯分量的方差，且满足：

2.3对新生目标进行预测：

其中，γ_k(x)表示在k时刻时的新生目标后验概率强度；J_γ,k表示新生目标在k时刻的高斯分量的个数；表示在k时刻第i个高斯分量的权重；表示期望为方差为的第i个高斯分量对应的高斯密度函数；

步骤3：利用接收的数据进行目标状态的更新；

3.1序贯式融合模型：

对多部雷达接收到的数据根据时间序列进行依次更新：

其中，分别表示k时刻第N次更新后和预测后的强度函数；和分别表示k时刻第N次预测时的幸存强度函数、衍生强度函数和新生强度函数；N表示雷达总数；表示k时刻第N次预测后的强度函数；p_D,k表示雷达检测概率；表示时刻第i部雷达的量测集合；J_k|k-1表示k时刻预测状态对应的高斯分量的个数；和分别表示k时刻利用第i部雷达的量测更新后第j个高斯分量的权重、均值和方差；和分别表示表示k时刻利用第i部雷达的第j个高斯分量的权重、均值和方差；κ_k(z)表示k时刻的杂波密度；H_k表示k时刻的状态转移矩阵；R_k表示k时刻的量测噪声协方差矩阵；

3.2固定节点的分布式融合模型：

对于第i∈{1,...,N}部雷达：

其中，分别表示第i部雷达在第k时刻更新后和预测后的状态；表示时刻第i部雷达的量测集合；p_D,k表示雷达检测概率；J_k|k-1表示k时刻预测状态对应的高斯分量的个数；和分别表示k时刻利用第i部雷达的量测更新后第j个高斯分量的权重、均值和方差；κ_k(z)表示k时刻的杂波密度；表示量测为z时对应的高斯函数的值；

多部雷达分别更新后，分别找出其距离融合节点最近的局部后验密度，然后采用广义协方差交叉算法进行融合处理，得到融合结果：

其中，s_k(x)表示融合后的强度函数；N_a和N_b分别是雷达a和b的高斯分量在第k个融合节点的个数；ω表示雷达a的权重；和分别表示雷达a和b距第k个融合节点最近的局部后验密度的过程噪声协方差矩阵；F_a,k、和F_b,k、分别表示雷达a和b距第k个融合节点最近的局部后验密度的状态转移矩阵及其转置；和分别表示融合前雷达a和雷达b的均值和协方差；和分别表示雷达a距第k个融合节点最近的局部后验密度预测后的权重、均值和方差；和分别表示雷达b距第k个融合节点最近的局部后验密度预测后的权重、均值和方差；和分别表示雷达a和b在第k个融合节点的融合后的权重、均值和方差。

步骤4：高斯分量的剪枝处理；

T是设定的门限。

剪枝循环开始：

I:＝I\L

直到时结束剪枝循环处理。

其中，L是满足门限的高斯分量集合；是剪枝前的高斯分量的权重、均值和方差；和是剪枝后的高斯分量的权重、均值和方差。

步骤5：目标个数和状态提取；

剪枝处理后的高斯分量，满足权重值大于0.5的高斯分量即是目标状态。

通过上面的步骤，就可以得到基于随机集理论下的异步数据处理过程，实现对机动多目标的跟踪及运动模型的估计。