单向耦合分数阶自持机电地震仪系统的模拟电路

本发明属于地震仪系统控制技术领域，涉及一种单向耦合分数阶自持机电地震仪系统的模拟电路。

背景技术：

具有复杂动力学特征的自持式机电地震仪系统属于一种敏感仪器，它能记录以一定频率传播的地面运动和波。研究其在不同工况下的多稳定性、混沌振荡、突跳和吸合等非线性动力学具有重要的现实意义。它的分数阶建模可以比整数阶建模更能精确地描述工程对象的真实运动过程。鉴于模拟电路实现简单、易于建模等优点，有必要构建模拟实验电路来验证动力学分析的结果。

到目前为止，只有零星的参考文献报道了这种地震记录系统，同时它们主要集中在混沌控制方面。siewe等人首先用多尺度方法讨论了非线性动力学，并通过阻尼作用控制了地震仪系统的混沌。他们随后应用梅尔尼科夫理论来抑制这个系统的不稳定性。hegaz用多尺度方法研究了地震仪系统的非线性振荡。然而，他们的工作仅限于地震仪系统的整数阶模型，不能很好地反映系统的运行过程。同时，混沌控制方法高度依赖于精确的数学建模，而这在实际应用中是不切实际的。此外，不涉及围绕地震仪动态特性的等效模拟电路和实验分析。鉴于此，许多研究者采用响应速度快、重现性好的电子模拟电路来验证混沌系统的数值研究。自治电路和地图电子电路被提出来揭示各种非线性行为。然而，由于没有考虑积分运算放大器和反相比例运算放大器，这两种方法都很难应用于复杂的动态系统。为了解决上述限制，埃尔-赛义德等人构建了一个新的4d系统的电路，萨巴拉辛纳姆和赛米兰设计了一个杜芬型微机电系统谐振器的模拟电路。但它们并没有解决电磁干扰和分数阶电路实现的困难。

技术实现要素：

有鉴于此，本发明的目的在于提供一种单向耦合分数阶自持机电地震仪系统的模拟电路，它能准确描述系统的动态特性，提高设计自由度，实现分数阶特性。

为达到上述目的，本发明提供如下技术方案：

一种单向耦合分数阶自持机电地震仪系统的模拟电路，包括：驱动系统电路和响应系统电路，通过耦合项电路连接；

所述驱动系统电路和响应系统电路分别包括：一个外部谐波激励信号、两个电压求和电路(如r1、r2、r13～r16，或r28～r33)、四个分数阶比例积分等效运算放大电路、四个反相比例运算放大电路、三个乘法器部分；

电压求和电路ⅰ的第一输入端接入外部谐波激励信号，所述电压求和电路ⅰ的输出端与分数阶比例积分等效运算放大电路ⅰ、反相比例运算放大电路ⅰ、分数阶比例积分等效运算放大电路ⅱ和反相比例运算放大电路ⅱ、乘法器部分ⅰ构成环形连接；所述反相比例运算放大电路ⅰ的输出端还与电压求和电路ⅰ的第二输入端连接；电压求和电路ⅱ的输出端依次与分数阶比例积分等效运算放大电路ⅲ、反相比例运算放大电路ⅲ、分数阶比例积分等效运算放大电路ⅳ和反相比例运算放大电路ⅳ连接；所述乘法器部分ⅱ的输入端与反相比例运算放大电路ⅲ的输出端连接，所述乘法器部分ⅱ的输出端与电压求和电路ⅱ的输入端连接；所述乘法器部分ⅲ的输入端与反相比例运算放大电路ⅳ的输出端连接，所述乘法器部分ⅲ的第一输出端与电压求和电路ⅱ的输入端连接，其第二输出端与耦合项电路连接。进一步，所述耦合项电路包括：一个同相比例运算放大电路(如u17和r77)和一个电压求和电路ⅲ(如r79和r80)；所述电压求和电路ⅲ的输入端分别与驱动系统电路的乘法器部分ⅲ的输出端和响应系统电路连接；所述电压求和电路ⅲ的输出端连接有同相比例运算放大电路。

进一步，所述分数阶比例积分等效运算放大电路ⅰ和分数阶比例积分等效运算放大电路ⅲ结构相同，均由两个电容(如c5～c6，或c9～c10)、两个定值电阻(如r3、r17，或r35～r36)和一个反相放大器(如u1a或u5a)组成；所述两个电容分别与一个电阻并联，然后串联，串联后的电容两端与反相放大器的反向输入端和输出端连接；

所述分数阶比例积分等效运算放大电路ⅱ和分数阶比例积分等效运算放大电路ⅳ结构相同，均由两个电容(如c7～c8，或c11～c12)、两个定值电阻(如r18、r34，或r37～r38)、三个定值电阻(如r7～r9，或r22～r24)和一个反相放大器(如u3a或u7a)组成；所述两个电容分别与一个电阻并联，然后串联，串联后的电容两端与反相放大器的反向输入端和输出端连接；其中一个定值电阻两端分别与反相放大器的正向输入端和接地端连接。

进一步，四个反相比例运算放大电路结构相同，均由三个定值电阻(如r4～r6，或r10～r12，或r19～r21，或r25～r27)和一个反相运算放大器(如u2a、u4a、u6a或u8a)组成；其中一个定值电阻的两端分别与反相运算放大器的反向输入端和输出端连接，另两个定值电阻分别与反相运算放大器的输入端连接。

进一步，所述电压求和电路ⅰ由六个定值电阻组成；所述电压求和电路ⅱ由六个定值电阻组成。

进一步，所述乘法器部分ⅰ由三个乘法器(如a1～a3)组成；所述乘法器部分ⅱ由两个乘法器(如a7～a8)组成；

所述驱动系统电路中的乘法器部分ⅲ由四个乘法器(如a4～a6、a9)组成，所述响应系统电路中的乘法器部分ⅲ由三个乘法器组成。

进一步，所述分数阶比例积分等效运算放大电路由单元电路构成，设计实现单元电路的相应传递函数h(s)为：

其中，co表示电容参数，ca和cb表示选定的电容，ra和rb表示选定的电阻，s表示拉普拉斯算子。

进一步，所述运算放大器两端的电压vi,i＝1,…,4对应驱动自持机电地震仪系统动力学方程中变量xi,i＝1,…,4，或对应响应自持机电地震仪系统动力学方程中的变量yi,i＝1,…,4；

驱动自持机电地震仪系统动力学方程为：

其中，x1＝xc，x3＝xz，表示α＞0的卡普托导数，ωm表示无量纲参数，ωe、xc和xz表示无因次变量，a0、a1和a2表示线性、三次和五次弹簧系数，m、b和l分别表示电线的质量、磁场和长度，f0和ω表示激励的振幅和频率，x表示非线性弹簧的伸长，l表示线性电感，α、r和i0分别表示分数阶系数、电阻和初始电流，oc和od表示非线性电容器的平均系数，q0表示参考电荷，c0表示电容器的线性部分，μ0表示阻尼系数；

响应自持机电地震仪系统动力学方程为：

其中，k＝r/rc表示电阻耦合参数。

进一步，乘法器用于产生非线性项驱动自持机电地震仪系统或响应自持机电地震仪系统中的非线性项。

本发明的有益效果在于：本发明建立的单向耦合分数阶自持机电地震仪系统的模拟电路，它能准确描述系统的动态特性，提高设计自由度，实现了分数阶特性；而且本发明构建的模拟电路观测结果与动力学分析结果吻合度高。

本发明的其他优点、目标和特征在某种程度上将在随后的说明书中进行阐述，并且在某种程度上，基于对下文的考察研究对本领域技术人员而言将是显而易见的，或者可以从本发明的实践中得到教导。本发明的目标和其他优点可以通过下面的说明书来实现和获得。

附图说明

为了使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明作优选的详细描述，其中：

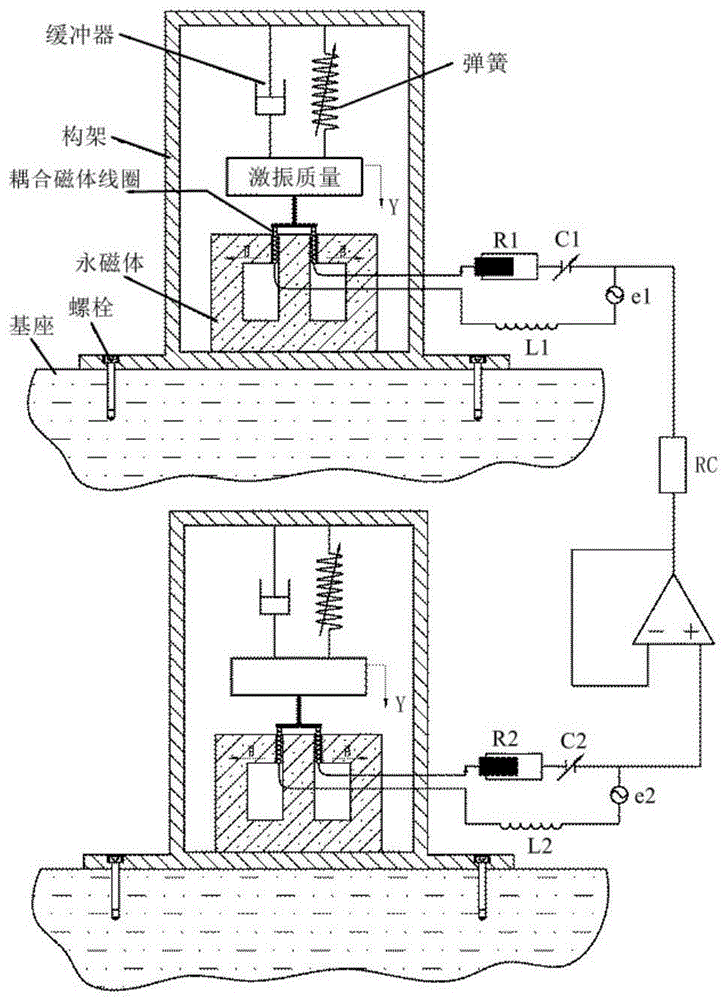
图1为单向耦合分数阶自持机电地震仪系统的示意图；

图2为单向耦合分数阶自持机电地震仪系统的模拟电路整体框架图；

图3为单向耦合分数阶自持机电地震仪系统的模拟电路的电路图；

图4为模拟电路中单个驱动自持机电分数阶地震仪系统的相图；

图5为模拟电路中单个响应自持机电分数阶地震仪系统的相图；

图6为模拟电路中单向耦合分数阶自持机电地震仪系统中响应系统的相图；

图7为单个驱动自持机电地震仪系统的相图；

图8为单个响应自持机电地震仪系统的相图；

图9为单向耦合分数阶自持机电地震仪系统中响应系统的相图。

具体实施方式

以下通过特定的具体实例说明本发明的实施方式，本领域技术人员可由本说明书所揭露的内容轻易地了解本发明的其他优点与功效。本发明还可以通过另外不同的具体实施方式加以实施或应用，本说明书中的各项细节也可以基于不同观点与应用，在没有背离本发明的精神下进行各种修饰或改变。需要说明的是，以下实施例中所提供的图示仅以示意方式说明本发明的基本构想，在不冲突的情况下，以下实施例及实施例中的特征可以相互组合。

其中，附图仅用于示例性说明，表示的仅是示意图，而非实物图，不能理解为对本发明的限制；为了更好地说明本发明的实施例，附图某些部件会有省略、放大或缩小，并不代表实际产品的尺寸；对本领域技术人员来说，附图中某些公知结构及其说明可能省略是可以理解的。

本发明实施例的附图中相同或相似的标号对应相同或相似的部件；在本发明的描述中，需要理解的是，若有术语“上”、“下”、“左”、“右”、“前”、“后”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此附图中描述位置关系的用语仅用于示例性说明，不能理解为对本发明的限制，对于本领域的普通技术人员而言，可以根据具体情况理解上述术语的具体含义。

请参阅图1～图9，本发明构建了与模拟电路密切相关的单向耦合分数阶自持机电地震仪系统动力学模型。它的模拟电路由驱动系统电路、响应系统电路和耦合项电路三部分组成。驱动系统电路和响应系统电路各由四个积分运算放大器、四个反相比例运算放大器、一个外部谐波激励信号、四组电容电阻并串联组成的分数阶比例积分等效运算放大电路、九个能产生非线性项的ad633乘法器、六个具有抑制由积分漂移引起的饱和或截止行为的积分漂移电阻、六个补偿偏置电流偏移的静态平衡电阻和18个由普通色环电阻与精密可调电位器构成的组合体组成。耦合项电路由一个同相比例运算放大电路和一个电压求和电路ⅲ组成。

实施例1：

1、构建系统动力学模型

单个分数阶自持机电地震仪系统通常由电气部分和机械部分两部分组成。其电气部分包括线性电感l、非线性电容cnl、非线性电阻rnr和与前三个电子元件串联安装的电动势ev。它的机械部分悬挂在外壳上，由一个减震器、一个地震质量和一个可调弹簧组成。这两个部分通过耦合磁体线圈和磁体耦合，从而产生磁场westerlund和ekstam利用实验结果揭示了电容器不同电介质的分数阶特性，例如其中c0,τ,和分别表示电容器的线性部分、时间、电流和电压。

与非线性电阻和电容相关的电压可以用分数阶的形式表达

其中，α,q,r和i0分别表示分数阶系数、电荷、电阻和初始电流，oc和od表示非线性电容器的平均系数，d^αq/dτ^α＝i，i为电流。

在实际应用中，摩擦和空气阻力都存在于调速系统中是不可避免的。因此，对于单个地震仪系统，具有非线性刚度的弹簧力可以写成

fd＝a0+a1x²+a2x⁴(2)

其中x表示非线性弹簧的伸长，a0,a1和a2表示线性、三次和五次弹簧系数。

由于永磁体和耦合线圈之间强相互作用的影响，应该考虑机械部分的拉普拉斯力和电气部分的楞次电动势。利用牛顿第二定律和基尔霍夫定律，建立单个分数阶机电地震仪系统的动力学方程

其中，m、b和l分别表示电线的质量、磁场和长度，f1、f0和ω表示激励的临界力、振幅和频率。

图1展示了单向耦合分数阶自持机电地震仪系统，其中使用线性电阻器和电流跟随器来连接两个分数阶地震仪系统(其中一个称为响应自持机电地震仪系统，另一个称为驱动自持机电地震仪系统)。

引入几个无量纲变量：

xc＝x/l，xz＝q/q0，t＝τ/we，

其中，q0表示参考电荷。

由(3)和(4)导出了卡普托分数阶定义下的陀螺耦合驱动系统控制方程，该方程能很好地处理零初始条件问题，则

其中无量纲参数设置为：x1＝xc，x3＝xz，表示α＞0的卡普托导数，ωm表示无量纲参数，ωe、xc和xz表示无因次变量，a0、a1和a2表示线性、三次和五次弹簧系数，m、b和l分别表示电线的质量、磁场和长度，f0和ω表示激励的振幅和频率，x表示非线性弹簧的伸长，l表示线性电感，α、r和i0分别表示分数阶系数、电阻和初始电流，oc和od表示非线性电容器的平均系数，q0表示参考电荷，c0表示电容器的线性部分，μ0表示阻尼系数。

响应自持机电地震仪系统动力学方程写成

其中，k＝r/rc表示电阻耦合参数。

2、模拟电路设计与动力学分析验证

驱动自持机电地震仪系统的物理参数定义为：μ1＝0.1，μ2＝0.2，ω1＝1，λ1＝0.01，λ2＝-0.7，β1＝0.01，β2＝0.1，γ1＝0.25，γ2＝0.9，ω＝0.5，f0＝1.2；

响应自持机电地震仪系统的物理参数定义为：μ1＝0.03，μ2＝0.02，ω1＝1，λ1＝0.5，λ2＝0.6，β1＝0.05，β2＝0.13，γ1＝0.65，γ2＝0.4，ω＝0.25，f0＝13.6。

基于能量流理论，单向耦合分数阶自持机电地震仪系统的微分方程与其电路微分方程一致。这一事实对动力学和电学测量技术的理论分析非常有用。采用频率近似的方法，来求解分数阶微分方程，给出单向耦合分数阶自持机电地震仪系统的动力学解析结果。ω在0.01±100rad/秒范围内，存在一个最大失真为0.2db的近似表达式

可以实现的单元电路。在模拟电路中给出了实现单元电路的相应传递函数h(s)：

其中，co表示电容参数，ca和cb表示选定的电容，ra和rb表示选定的电阻。在单向耦合分数阶自持机电地震仪系统中ca＝10.0022nf，cb＝208.054nf，ra＝976.784mω和rb＝448.251kω。

由驱动系统、耦合项和响应系统组成的单向耦合分数阶自持机电地震仪系统的模拟电子电路如图3所示。运算放大器(tl074cn)两端的电压vi,i＝1,…,4在驱动自持机电地震仪系统中起着变量xi,i＝1,…,4的作用。类似地，运算放大器两端的电压vi_1,i＝1,…,4在响应自持机电地震仪系统中扮演变量yi,i＝1,…,4的角色。在电路中，17个ad633乘法器用于产生非线性项，如驱动自持机电地震仪系统中的和响应自持机电地震仪系统中的设计了同相比例运算放大电路，实现了驱动和响应自持机电地震仪系统的耦合。采用四个积分运算放大器和四个反相比例运算放大器来产生积分和反相器作用。外部谐波信号f0cosωt的驱动幅值f0等于激励幅值。

应用基尔霍夫定律，写出了图3中的电路方程

电路方程(9)-(10)与动力学方程(5)等同，电路方程(11)-(12)与动力学方程(6)等同。

r9,r24,r44和r58代表积分漂移电阻，可以抑制由积分漂移引起的饱和或截止行为。引入静态平衡电阻，如r5,r8,r11,r20,r23,r26,r40,r43,r46,r54,r57和r60，以补偿偏置电流的偏移。图3给出了所有实验电路元件的参数与规格。所有电阻是由普通色环电阻与精密可调电位器构成的组合体。

实验时采用振幅为f0的小余弦电压来激励地震仪系统。在电子模拟电路中，图4～图5描述了单个驱动和响应自持机电分数阶地震仪系统的相图。图6展示了单向耦合分数阶自持机电地震仪系统中响应自持机电地震仪系统的相图。很明显，该系统可以在不同情况下产生瞬态混沌、倍周期运动和相对混沌振荡的瞬态响应。模拟电路观测结果与动力学分析结果(即图4与图7、图5与图8、图6与图9)对比，发现两图之间高度吻合，说明了本发明所构建单向耦合分数阶自持机电地震仪系统模拟电路的有效性与科学性。

最后说明的是，以上实施例仅用以说明本发明的技术方案而非限制，尽管参照较佳实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，可以对本发明的技术方案进行修改或者等同替换，而不脱离本技术方案的宗旨和范围，其均应涵盖在本发明的权利要求范围当中。