一种高速受电弓多目标鲁棒H∞控制器设计方法与流程

本发明涉及高速铁路接触网领域，特别涉及一种高速受电弓多目标鲁棒H∞控制器设计方法。

背景技术：

电气化铁路中，电力机车运行时顶部受电弓与接触网之间的接触压力是表征其受流质量的重要指标。接触压力反应了受电弓和接触线之间的接触质量，接触压力过小会使弓网间产生电弧或电火花，甚至导致弓网离线。接触压力过大则会加剧受电弓弓头和接触线的磨损，可能导致刮弓事故的发生。不良的接触压力不仅会影响电力机车的受流质量，同时也会加剧弓网系统机械性能的损耗，从而降低其使用寿命，严重时会造成弓网系统的损坏致机车停止运行。因此，随着运行速度的提高，降低接触力波动成为确保弓网系统安全可靠运行的关键环节之一，受电弓主动控制是实现这一目标的有效措施。

控制器设计是受电弓主动控制研究的关键内容。国外方面，Lin等针对城市轻轨系统受电弓提出了线性二次型调节器，并研究了考虑作动器时滞的最优控制。Sanchez等提出了不同配置的PID控制器，综合考虑了接触力和控制所耗能量。Yamashita等提出了阻抗控制器，其将受电弓框架位移作为反馈信号，性能较PID控制器更优。Pisano等提出了基于二阶滑模的输出反馈控制器，并将其作用于一个实际受电弓。Allotta等测试了PD控制器在T2006型受电弓上的性能。Collina等研究了接触力前馈控制器。Walters等提出了模糊控制器和模糊PID控制器。Chater等提出了基于Backstepping的输出反馈控制器。国内方面，吴燕等提出了bang-bang控制。张晓东等提出了受电弓自适应控制。杨岗等提出了基于LQR的受电弓半主动控制。

上述控制方法在一定程度上减小了接触力波动，但仍存在以下问题：一是没考虑状态量的获取途径，弓网系统运行环境极为复杂，状态量测十分困难，在某些工况下不允许安装测量设备；二是控制目标仅针对接触力的波动，实际上作动器不能输出任意大小的控制力，而且受电弓弓头抬升量在相关标准中也有规定；三是控制器的鲁棒性不能得到保证，而弓网系统又极易受外界环境干扰。

技术实现要素：

本发明所要解决的技术问题是提供一种高速受电弓多目标鲁棒H∞控制器设计方法，以降低高速铁路中的弓网接触力波动。

为解决上述技术问题，本发明采用的技术方案是：

一种高速受电弓多目标鲁棒H∞控制器设计方法，包括以下步骤：

步骤1：建立受电弓-接触网系统的数学模型，具体包括：

步骤1.1：建立接触网的非线性有限元数学模型，即将接触网的有限元模型写为基本的动力学平衡方程；

步骤1.2：建立简化的接触网数学模型，即由接触网的非线性有限元模型，得到接触线的静态刚度曲线，通过数值拟合方法得到其静态刚度数学模型，拟合公式为：

式中：t表示受电弓运行时间，v表示受电弓运行速度，k(t)表示接触线在vt处的静态刚度，a_i、b_i、c_i为拟合系数；

步骤1.3：建立受电弓的三自由度数学模型

将受电弓弓头、上框架和下框架分别等效为集中质量点，各个质量点之间由并联的阻尼器和弹簧连接；弓头质量点受向下的接触力作用，下框架质量点受静态抬升力和主动控制力作用；根据动力学分析，建立受电弓三自由度数学模型；

步骤1.4：受电弓与接触网的耦合数学模型，即接触力的计算，采用罚函数法；

步骤2：设计受电弓状态估计器，具体包括：

步骤2.1：建立弓网系统状态空间模型

式中：‘T’表示矩阵的转置；w_r表示系统受到的外界扰动，A、B₁、B₂、C₁为系数矩阵，由受电弓的三自由度数学模型得到，C₁＝[k(t),0,0,0,0,0]，z₁为输出；

步骤2.2：建立面向状态估计的弓网数学模型

弓网系统状态空间模型离散化，取消外界扰动项B₁w_r，增加系统噪声项w_k和量测噪声项v_k，得面向状态估计的弓网系统数学模型：

式中：y_k为测量输出，γ_k表示随机量测丢失，C_k＝[1,0,1,0,1,0]，x_k、A_k、B_k、u_k分别与x、A、B₂、u对应；

步骤2.3：设计受电弓状态估计器

测量受电弓弓头、上框架和下框架的位移，测量值包含噪声，通过以下步骤获得受电弓弓头、上框架和下框架的位移与加速度；

如果γ_k+1＝0,

P_k+1|k+1＝A_k(0)P_k|kA_k^T(0)+B_k(0)Q_kB_k^T(0)

如果γ_k+1＝1,

式中：‘^’表示原矩阵或变量对应的估计值，下标‘k’和‘k+1’表示该变量在第k次和k+1次的迭代结果，y_k+1表示观测值，x_k+1表示状态值，Q_k和R_k分别为w_k和v_k的协方差矩阵，P_k|k、l_k、S_k、T_k为过程变量，A_k、B_k、C_k为离散状态空间方程的系数矩阵；

步骤3：设计多目标鲁棒H_∞控制器，具体包括：

步骤3.1：确定控制目标；

步骤3.2：建立面向控制的弓网数学模型，根据状态空间模型建立面向控制的增广矩阵模型：

式中：

步骤3.3：设计多目标鲁棒H_∞控制器

给定标量ρ和r，如果存在正定矩阵P>0和Q满足下列线性矩阵不等式

则状态反馈增益矩阵表示为：K＝QP^-1，式中：‘*’表示矩阵对应块的转置，为弓网系统增广矩阵的系数矩阵。

根据上述方案，控制增益矩阵由增广的弓网系统状态空间方程通过求解线性矩阵不等式得到。

根据上述方案，估计器的引入使得不需要测量所有的受电弓状态反馈信号，且该估计器接受一定概率的量测数据丢失。

与现有技术相比，本发明的有益效果是：

1、本发明针对高速受电弓这一强非线性系统，引入了鲁棒H∞控制，保证了控制过程的鲁棒性和稳定性，提高了控制性能。

2、本发明考虑了主动控制力的大小和对受电弓弓头抬升量的影响，有利于其实际应用。

3、本发明通过估计器获得状态反馈信号，且估计器接受一定概率的量测丢失，更加贴近于实际应用。

附图说明

图1为本发明高速受电弓多目标鲁棒H∞控制器设计流程图。

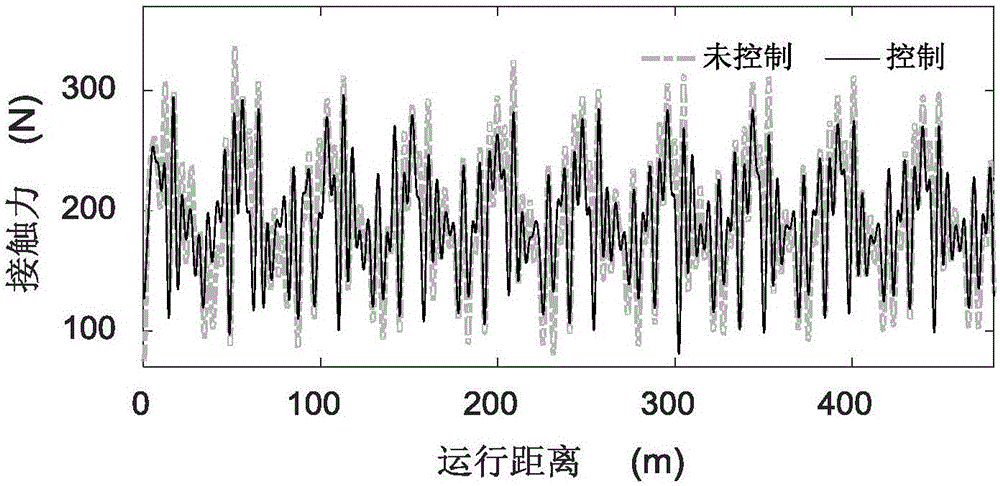
图2为运行速度为360km/h时的接触力控制效果图。

图3为运行速度为320km/h时的接触力控制效果图。

图4为运行速度为300km/h时的接触力控制效果图。

图5为运行速度为280km/h时的接触力控制效果图。

图6为不同速度下的接触力标准差统计图。

图7为不同速度下的接触力平均值统计图。

图8为360km/h时的主动控制力。

图9为控制前后接触网上弓头处的垂向位移。

图10为控制前后接触网上支柱处的垂向位移。

图11为控制前后接触网上第一根吊弦处的垂向位移。

图12为控制前后接触网上跨中处的垂向位移。

具体实施方式

下面结合附图和具体实施方式对本发明作进一步详细的说明。本发明的估计器可以得到受电弓的各个状态信息，并将此作为反馈信号，多目标控制使得所设计的控制器更有利用实际应用，鲁棒H∞控制使得控制器的鲁棒性得到保证。本发明方法详述如下：

一、建立受电弓-接触网系统的数学模型

1、建立接触网的非线性有限元数学模型

以京津线接触网参数为依据，将接触线和承力索当作非线性索单元，将吊弦当作非线性杆单元，建立接触网的有限元模型，写为基本的动力学平衡方程：

式中：M_c、C_c、K_c分别为接触网单元的全局质量、全局阻尼和全局刚度矩阵，x_c分别为有限单元节点的加速度、速度和位移矩阵，f_c为接触网的外力向量。

接触线/承力索数学模型：

式中：l_cx、l_cy、l_cz分别表示一个接触线/承力索单元的两个端点在x、y、z方向的相对位置，F_c1、F_c2、F_c3分别表示一个接触线/承力索单元的左端点在x、y、z方向的节点力，F_c4、F_c5、F_c6分别表示一个接触线/承力索单元的右端点在x、y、z方向的节点力，l_c0表示一个接触线/承力索单元的初始长度，E_c表示接触线/承力索的弹性模量，A_c表示接触线/承力索的横截面积，w_c表示一个接触线/承力索单元的自重。

吊弦数学模型：

式中：F_t1、F_t2、F_t3分别表示一个杆单元的左端点在x、y、z方向的节点内力，L_tx、L_ty、L_tz分别表示一个杆单元的两个端点在拉升状态下在x、y、z方向的相对位置，L_t0表示一个杆单元在非拉升状态下的初始长度，E_t表示吊弦的弹性模量，A_t表示吊弦的横截面。

2、建立简化的接触网数学模型

由接触网的非线性有限元模型，得到接触线的静态刚度曲线，通过数值拟合方法得到其静态刚度数学模型，拟合公式为：

式中：t表示受电弓运行时间，v表示受电弓运行速度，k(t)表示接触线在vt处的静态刚度，a_i、b_i、c_i为拟合系数。

3、建立受电弓三自由度数学模型

以DSA380型受电弓参数为依据，将受电弓弓头、上框架和下框架分别等效为集中质量点，各个质量点之间由并联的阻尼器和弹簧连接。弓头质量点受向下的接触力作用，下框架质量点受静态抬升力和主动控制力作用，建立受电弓三自由度数学模型。

式中：m₁、m₂、m₃分别表示受电弓弓头、上框架和下框架的等效质量，x₁、x₂、x₃分别表示受电弓弓头、上框架和下框架的垂向位移，分别表示受电弓弓头、上框架和下框架的垂向加速度，即对相应变量求导，F_l表示受电弓静态抬升力，u表示主动控制力。

4、受电弓与接触网的耦合数学模型

即弓网接触力F(t)的计算，针对非线性有限元的接触网模型：

式中：k_s表示接触刚度，本实例中取值为82300N/m，x_c表示接触点处的接触线垂向位移，F(t)表示t时刻的接触力。

针对简化的接触网模型：

F(t)＝x₁k(t)

二、受电弓状态估计

1、建立弓网系统状态空间模型

选取受电弓三个质量点的垂向位移和垂向加速度作为状态变量，结合简化的接触网数学模型，并将主动控制力作为系统输入，弓网接触力作为系统输出，增加系统外界扰动项，建立弓网系统状态空间模型。

式中：‘T’表示矩阵的转置，w_r表示系统受到的外界扰动，A、B₁、B₂、C₁为系数矩阵，由受电弓的三自由度数学模型得到，C₁＝[k(t),0,0,0,0,0]；z₁为输出。

2、建立面向状态估计的弓网数学模型

将简化接触网模型下的弓网系统状态空间模型离散化，取消外界扰动项B₁w_r，增加系统噪声项w_k和量测噪声项v_k，得面向状态估计的弓网系统数学模型：

式中：y_k为测量输出，γ_k表示随机量测丢失，C_k＝[1,0,1,0,1,0]，x_k、A_k、B_k、u_k分别于x、A、B₂、u对应。

3、受电弓状态估计器

测量受电弓弓头、上框架和下框架的位移，测量值包含噪声，通过以下步骤获得受电弓弓头、上框架和下框架的位移和加速度。

如果γ_k+1＝0,

P_k+1|k+1＝A_k(0)P_k|kA_k^T(0)+B_k(0)Q_kB_k^T(0)

如果γ_k+1＝1,

式中：‘^’表示原矩阵或变量对应的估计值，下标‘k’和‘k+1’表示该变量在第k次和k+1次的迭代结果，y_k+1表示观测值，x_k+1表示状态值，Q_k和R_k分别为w_k和v_k的协方差矩阵，P_k|k、l_k、S_k、T_k为过程变量，A_k、B_k、C_k为离散状态空间方程的系数矩阵。

三、多目标鲁棒H_∞控制器

1、控制目标的确立

主要目标为降低接触力波动，即减小实时接触力与参考接触力之间的差值：

e(t)＝F_r-F(t)

式中：e(t)为实时接触力F(t)与参考接触力F_r之间的差值，本实例中参考接触力为其平均值。

第二目标为将主动控制力限制在合理范围内：

|u(t)|≤u_max

式中：u_max为允许的最大控制力，本实例中，取200N。

第三目标为将弓头垂向位移限制在合理范围内：

|x₁(t)|≤x_1max

式中：x_1max为允许的弓头最大垂向位移，根据标准EN 50367最大值取0.1m。

2、建立面向控制的弓网系统模型

将接触力的跟踪误差作为状态变量，增广至简化的状态空间模型，根据控制目标设置系统输出，建立面向控制的弓网系统模型：

式中：

3、多目标鲁棒H_∞控制器

给定标量ρ和r，如果存在正定矩阵P>0和Q满足下列线性矩阵不等式

则状态反馈增益矩阵可表示为：K＝QP^-1。式中：‘*’表示矩阵对应块的转置，为弓网系统增广矩阵的系数矩阵。

结合状态估计器和控制器，主动控制力u(t)即表示为：

最后，在Matlab中验证其性能，图2至图5为运行速度为360km/h、320km/h、300km/h和280km/h时的接触力控制效果图，其对应的接触力标准差分别降低20.6％、16.3％、24.8％和21.8％；图6和图7分别为不同速度下的接触力标准差和平均值统计图，采用本发明方法设计的控制器在不影响接触力平均值的情况下，大大降低了接触力波动。图8为运行速度360km/h时的主动控制力，可见其均小于允许的最大控制力200N；图9至图12为控制前后接触网上几个关键位置的垂向位移比较，可见采用本发明方法所设计的控制器，不仅减小了接触力波动，而且在一定程度上抑制接触网振动。