基于连续功率谱分析的电力负荷预测优化方法与流程

本发明属于电力系统
技术领域：
，具体涉及一种基于连续功率谱分析的电力负荷预测优化方法。
背景技术：
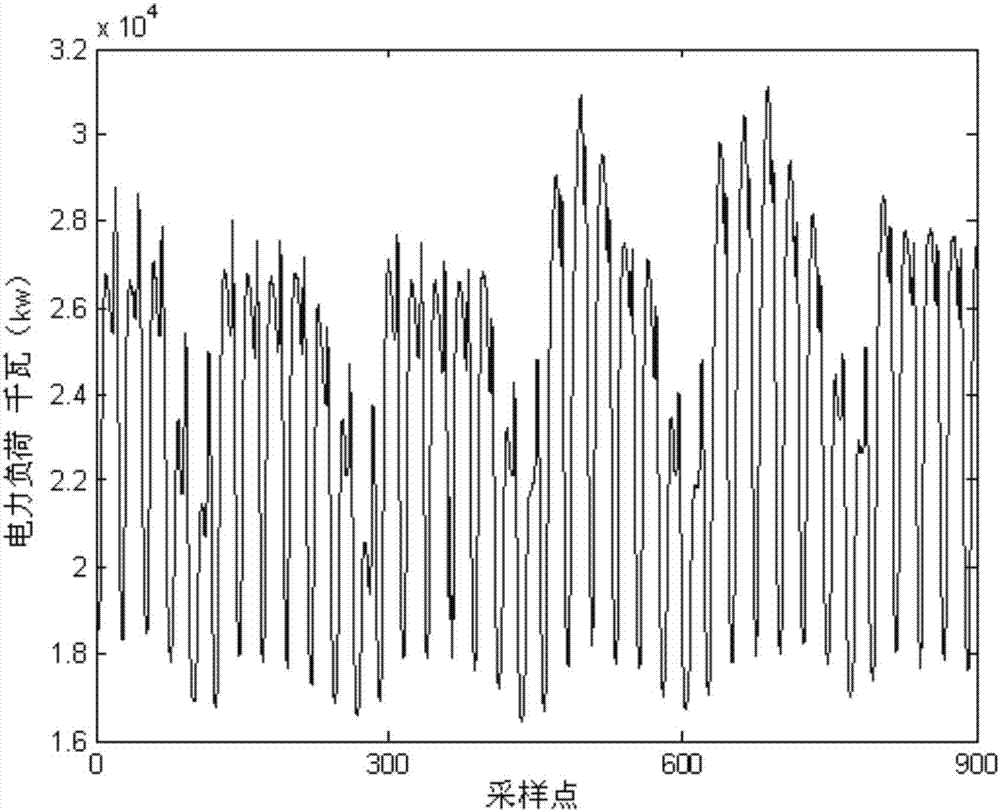
：电力系统负荷是指系统中所有用电设备消耗功率的总和，也称电力系统综合用电负荷。综合用电负荷加上电网中的损耗和发电厂的厂用电，就是系统中所有发电机应发的总功率，也称电力系统发电负荷。电力负荷是影响系统安全稳定运行的重要因素。电力负荷预测是指通过对电力负荷历史记录的分析研究，综合考虑影响电力负荷变化的各种因素，如社会发展规划、经济状况、气象变化因素以及节假日等，对未来电力负荷的发展做出预先估计。电力负荷预测是电力系统规划、计划、调度、用电的依据。提高电力负荷预测技术水平，有利于制定合理的电源建设规划，有利于合理安排电网运行方式和机组检修计划，有利于节煤、节油和降低发电成本，有利于计划用电管理，有利于提高电力系统的经济效益和社会效益。因此，电力负荷预测是实现电力系统管理现代化的重要内容之一。由于受天气情况和人们社会活动等因素的影响，电力负荷数据存在大量的随机性和非线性关系，影响电力负荷时间序列的因素可划分为内在随机因素和外在随机因素，其中外在因素包括气象、社会、经济等，而内在因素是由电力系统内部非线性因素影响的结果，电力负荷是系统内在和外在随机性影响因素共同作用的结果，其预测不准确的原因不仅仅是外在随机因素的影响，更重要的是由系统内在动力学特征所决定。为此，涌现了多种预报方法，从一般统计模型，如arima时间序列模型、灰色模型等到各类智能模型，如神经网络模型、支持向量机模型等等，算法的改进有望提高电力负荷的预报精度，但最根本的还是在于所使用的预测方法对于数据的学习和泛化性能。电力负荷受人类生产生活影响具有明显的规律性，但这种规律性中又存在大量的随机性，影响模型的学习和泛化能力。技术实现要素：为了解决上述技术问题，本发明旨在提供一种基于连续功率谱分析的电力负荷预测优化方法，通过连续功率谱分析，提取原始电力负荷时间序列中隐含的显著周期序列并分离得到残差序列，由于显著周期序列占原序列比重大，并且规律性强，因此可以高精度预测，而残差序列由于占原序列比重小因而误差有限，从而保证了可以有效提高电力负荷预报的精度。实现上述技术目的，达到上述技术效果，本发明通过以下技术方案实现：一种基于连续功率谱分析的电力负荷预测优化方法，包括读入原始采样电力负荷时间序列，并按预报间隔要求将其转换为平均电力负荷时间序列，然后计算出平均电力负荷时间序列的距平序列；采用连续功率谱分析方法，提取平均电力负荷时间序列的距平序列中隐含的显著周期序列，并分离得到残差序列；采用粒子群算法优化的bp神经网络对显著周期序列进行预测，获得各显著周期序列的预测结果；采用粒子群算法优化的rbf神经网络对残差序列的一阶差分序列进行预测，后经差分反运算得到残差序列的预测结果；将平均电力负荷时间序列的平均值与各显著周期序列的预测结果以及残差序列的预测结果相加获得最终预测结果。进一步地，所述原始采样电力负荷时间序列为p＝{p(i),i＝1,2,...,n}，其中n为原始电力负荷采样点个数；所述平均电力负荷时间序列为p’＝{p’(j),j＝1,2,...,m}，其中m为按预报间隔要求转换后的平均电力负荷序列的采样点个数，p’的平均值为令所述平均电力负荷时间序列的距平序列为进一步地，所述显著周期序列为{p1,p2,…,pk,…,pk}，其中k为p中隐含的显著周期序列的个数，pk＝{pk(1),pk(2),…,pk(m)}，其中pk(1),pk(2),…,pk(m)分别为显著周期序列pk的值；所述残差序列为r＝p-p1-p2-…-pk。进一步地，所述采用连续功率谱分析方法，提取平均电力负荷时间序列的距平序列中隐含的显著周期序列，具体为：利用连续功率谱方法，分析平均电力负荷时间序列的距平序列的显著周期带，并利用快速傅立叶变换的频域滤波方法提取各显著周期带对应的时间序列，从而获得显著周期序列。进一步地，所述采用基于粒子群算法优化的bp神经网络对显著周期序列进行预测的具体过程为：(1)依据kolmogorov定理，建立3层bp神经网络模型，设输入层神经元个数为i，隐含层神经元个数为h，输出层神经元个数为o；其中，h＝2*i+1，o＝1；(2)确定需要优化的参数，包括：bp神经网络的输入层神经元个数i和训练集的长度l，还包括：w＝(w(1),w(2),...,w(q))，q＝i*h+h*o+h+o，其中，w(1)～w(i*h)为bp神经网络的输入层至隐含层神经元的连结权值，w(i*h+1)～w(i*h+h*o)为bp神经网络的隐含层至输出层神经元的连结权值，w(i*h+h*o+1)～w(i*h+h*o+h)为bp神经网络隐含层神经元的阈值，w(i*h+h*o+h+1)～w(i*h+h*o+h+o)为bp神经网络输出层神经元的阈值；(3)初始化种群x＝(x1,x2,...,xq1)，其中q1为粒子的总数，第i个粒子为xi＝(ii,wi,li)，粒子速度为vi＝(vii,vwi,vli)，其中ii、wi、li为参数i、w、l一组备选解；(4)根据群体中的每个粒子xi＝(ii,wi,li)确定的参数，构造bp神经网络训练集的输入和输出矩阵，其中针对显著周期序列pk及bp神经网络输入层神经元个数ii首先建立矩阵z1和z2，其中：针对待优化神经网络训练集长度l，z1中最后的li列作为训练集的输入矩阵itrain，z2中最后的li列作为训练集的输出矩阵otrain；将预报步长l作为测试步长，z1中最后的l列作为测试集的输入矩阵itest，z2中最后的l列作为测试集的输出矩阵otest；根据训练集构造的bp神经网络对测试集模拟结果的误差平方和作为其适应度值，以适应度值最小为优化方向作为评价标准评判各个粒子的优劣，记录粒子xi当前个体极值为pbest(i)，取群体中pbest(i)最优的个体作为整体极值gbest；(5)群体中的每个粒子xi，分别对其位置和速度进行更新；式中：ω为惯性权重，c1、c2为加速度因子，g为当前迭代次数，r1、r2为分布于[0,1]的随机数；(6)重新计算各个粒子此时的目标函数值，更新pbest(i)和gbest；(7)判断是否达到最大迭代次数，如满足则结束优化过程，获得经粒子群算法优化得到的参数最优值为(ibest,wbest(wbest(1),wbest(2),...,wbest(q)),lbest)，否则返回步骤(4)；(8)按ibest、wbest(wbest(1),wbest(2),...,wbest(q))、lbest构造bp神经网络训练集z3和测试集z4并初始化bp神经网络连结权值和阈值，其中：wbest(1)～wbest(i*h)为bp神经网络的输入层至隐含层神经元的连结权值的初始值，wbest(i*h+1)～wbest(i*h+h*o)为bp神经网络的隐含层至输出层神经元的连结权值的初始值，wbest(i*h+h*o+1)～wbest(i*h+h*o+h)为bp神经网络隐含层神经元的阈值的初始值，wbest(i*h+h*o+h+1)～wbest(i*h+h*o+h+o)为bp神经网络输出层神经元的阈值的初始值，就此建立起bp神经网络模型，经训练后进行迭代的l步预测，并获得对应的预测结果。进一步地，所述采用粒子群优化的rbf神经网络对残差序列的一次差分序列进行预测，具体过程为：(1)确定需优化参数，包括：rbf神经网络输入层神经元个数i和训练集的长度l；(2)初始化种群其中q2为粒子的总数，第i个粒子为xi＝(ii,li)，粒子速度为其中ii,li为参数i、l一组备选解；(3)根据群体中的每个粒子确定的参数，构造rbf神经网络训练集的输入和输出矩阵，其中针对残差序列r及rbf神经网络输入层神经元个数ii首先建立矩阵z5和z6，其中：针对待优化神经网络训练集长度l，z5中最后的li列作为训练集的输入矩阵itrain，z6中最后的li列作为训练集的输出矩阵otrain；将预报步长l作为测试步长，z5中最后的l列作为测试集的输入矩阵itest，z6中最后的l列作为测试集的输出矩阵otest；根据训练集构造的rbf神经网络对测试集模拟结果的误差平方和作为其适应度值，以适应度值最小为优化方向作为评价标准评判各个粒子的优劣，记录粒子xi当前个体极值为pbest(i)，取群体中pbest(i)最优的个体作为整体极值gbest；(4)群体中的每个粒子xi，分别对其位置和速度进行更新；式中：ω为惯性权重，c1、c2为加速度因子，g为当前迭代次数，而r1、r2为分布于[0,1]的随机数；(5)重新计算各个粒子此时的目标函数值，更新pbest(i)和gbest；(6)判断是否达到最大迭代次数，如满足则结束优化过程，获得经粒子群算法优化得到的参数最优值为(ibest,lbest)，否则返回步骤(3)。(7)按ibest和lbest构造rbf神经网络训练集z7和测试集z8，其中：就此建立起rbf神经网络模型，经训练后进行迭代的l步预测，并获得对应的预测结果。进一步地，所述惯性权重ω＝0.5，加速度因子c1＝c2＝1.49445。本发明的有益效果：(1)经连续功率谱分析提取的电力负荷显著周期序列由于规律性强，因此可以高精度的进行预测，而且显著周期序列在原电力负荷序列中所占比重较大，因此奠定了较高精度预测的基础；剔除了周期信号后的残差序列一方面由于在整体电力负荷序列中的比重不大，另一方面由于在处理的过程中进行了一次差分运算而变得平稳，其预测误差相对有限，因此本发明所提出的将电力负荷序列经连续功率谱分析，分解为多个显著周期序列和单个残差序列，进而对各个显著周期序列和残差序列分别进行预测的方法可以大大提高整体预测效果。(2)针对神经网络结构选择不一对于预报性能的影响，本发明针对电力负荷序列分离出的显著周期序列和残差序列的特点，分别采用bp神经网络和rbf神经网络，并对于神经网络的结构参数，训练集规模采用粒子群算法进行优化，显著改善了神经网络的泛化性能，最终提高了预测精度。附图说明图1为本发明的基于连续功率谱分析的电力负荷预测优化方法的流程图；图2为原始电力负荷序列图；图3为平均电力负荷时间序列的距平序列的连续功率谱分析结果图；图4为平均电力负荷时间序列的距平序列提取的显著周期序列及分离的残差序列图；图5(a)为本发明方法的一步预测结果图；图5(b)为本发明方法的二步预测结果图；图5(c)为本发明方法的三步预测结果图；图6(a)为针对原始电力负荷序列建立粒子群优化rbf神经网络一步预测结果图；图6(b)为针对原始电力负荷序列建立粒子群优化rbf神经网络二步预测结果图；图6(c)为针对原始电力负荷序列建立粒子群优化rbf神经网络三步预测结果图图7(a)为针对原始电力负荷序列建立的arima时间序列模型一步预测结果图；图7(b)为针对原始电力负荷序列建立的arima时间序列模型二步预测结果图；图7(c)为针对原始电力负荷序列建立的arima时间序列模型三步预测结果图。具体实施方式为了使本发明的目的、技术方案及优点更加清楚明白，以下结合实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。下面结合附图对本发明的应用原理作详细的描述。本发明的一种基于连续功率谱分析的电力负荷预测优化方法，采用连续功率谱分析方法，提取电力负荷时间序列中隐含的显著周期序列并分离得到残差序列，采用基于粒子群算法优化的bp神经网络对显著周期序列进行预测，获得各显著周期序列的预测结果，采用粒子群算法优化的rbf神经网络对残差序列的一阶差分序列进行预测，后经差分反运算得到残差序列的预测结果，最后将平均电力负荷时间序列的平均值与各显著周期序列的预测结果以及残差序列的预测结果相加获得最终预测结果。如图1所示，具体地，包括以下步骤：s1，读入原始采样电力负荷时间序列，并按预报间隔要求将其转换为平均电力负荷时间序列，然后计算出平均电力负荷时间序列的距平序列；所述原始采样电力负荷时间序列为p＝{p(i),i＝1,2,...,n}，其中n为原始电力负荷采样点个数；所述平均电力负荷序列为p’＝{p’(j),j＝1,2,...,m}，其中m为按预报间隔要求转换后的平均电力负荷序列的采样点个数，p’的平均值为令所述平均电力负荷时间序列的距平序列为s2，采用连续功率谱分析方法，提取平均电力负荷时间序列的距平序列中隐含的显著周期序列，并分离得到残差序列；所述显著周期序列为{p1,p2,…,pk,…,pk}，其中k为p中隐含的显著周期序列的个数，pk＝{pk(1),pk(2),…,pk(m)}，其中pk(1),pk(2),…,pk(m)分别为显著周期序列pk的值；所述残差序列为r＝p-p1-p2-…-pk；因此，p＝p1+p2+…+pk+r。上述的提取过程，具体如下：假设一离散时间序列为xt，其中t＝0,1,...,n-1，共n个采样点，时间间隔δt＝1，应用连续功率谱估计方法，分析该离散时间序列的显著周期带，并利用傅立叶变换fft的频域滤波方法提取各显著周期带对应的时间序列，具体包括以下步骤：(1)确定连续功率谱值首先计算xt连续功率谱粗谱估计值：其中：为h波数对应的连续功率谱粗谱估计值，h为波数，h＝0,1,…m，m＝n/8，r(τ)为时间序列xt的落后时间长度为τ的自相关系数：其中，和s分别为离散时间序列xt的平均值和标准差。为了消除粗谱估计值的小波动，对(1)式进行汉宁平滑，平滑后为连续功率谱值(即图3实线所示)为：s0为0波数对应的连续功率谱值；sh为h波数对应的连续功率谱值，sm为m波数对应的连续功率谱值。(2)确定分析周期h波数对应的周期为：(即图3横坐标对应的周期点)，本发明实施例中考虑m＝n8，则(3)连续功率谱信度检验将式(3)所得连续功率谱值与红噪音谱值进行比较，判断其显著性。假设式(3)所得连续功率谱值为某一非周期性过程谱值，h波数对应的连续功率谱值sh与平均红噪音谱值之比遵从被其自由度ν去除的χ2分布：其中平均红噪音谱值为：式中，为式(3)中计算所得的所有波数的连续功率谱值的平均值，r(1)为xt落后时间长度为1的自相关系数，而自由度ν为：本发明实施例选取在0.05显著性水平下，当时，该波数的谱值是显著的，则该周期波动是显著的，为图3中虚线检验线。(4)提取周期带对应的时间序列周期带的确定：取步骤(3)所选显著连续功率谱值左右两侧各第一个低于红噪音检测线的周期点，组成周期带，此周期带为显著周期带，其中图3中左侧第一低于红噪音检测线的点定为周期带的上界，图3中右侧第一低于红噪音检测线的点定为周期带的下界。周期带对应的时间序列的提取：本发明实施例采用中国科学院测量与地球物理研究所开发的地学数据处理程序库whiggf90lib(wfl)，通过应用该软件的傅立叶变换fft的频域滤波子程序，来提取周期带对应的时间序列，该子程序为：callfft_filter(n,x,dt,per1,per2,fil_method,xout)其中n为总采样点个数，x即为xt，dt为采样时间间隔δt，per1为提取周期带下界，per2为提取周期带上界，fil_method为滤波类型，这里取“band”，指代为带状周期，xout为提取的显著周期带对应的时间序列。s3，采用基于粒子群优化的bp神经网络对显著周期序列进行预测，其具体过程为；(1)依据kolmogorov定理，一个3层bp神经网络能够实现对任意非线性函数进行逼近，因此，本发明实施例建立3层bp神经网络模型，设输入层神经元个数为i，隐含层神经元个数为h，输出层神经元个数为o；其中，h＝2*i+1，o＝1；(2)确定需要优化的参数，包括：bp神经网络的输入层神经元个数i和训练集的长度l，还包括：w＝(w(1),w(2),...,w(q))，q＝i*h+h*o+h+o，其中，w(1)～w(i*h)为bp神经网络的输入层至隐含层神经元的连结权值，w(i*h+1)～w(i*h+h*o)为bp神经网络的隐含层至输出层神经元的连结权值，w(i*h+h*o+1)～w(i*h+h*o+h)为bp神经网络隐含层神经元的阈值，w(i*h+h*o+h+1)～w(i*h+h*o+h+o)为bp神经网络输出层神经元的阈值；(3)初始化种群x＝(x1,x2,...,xq1)，其中q1为粒子的总数，第i个粒子为xi＝(ii,wi,li)，粒子速度为vi＝(vii,vwi,vli)，其中ii、wi、li为参数i、w、l一组备选解；(4)根据群体中的每个粒子xi＝(ii,wi,li)确定的参数，构造bp神经网络训练集的输入和输出矩阵，其中针对显著周期序列pk及bp神经网络输入层神经元个数ii首先建立矩阵z1和z2，其中：针对待优化神经网络训练集长度l，z1中最后的li列作为训练集的输入矩阵itrain，z2中最后的li列作为训练集的输出矩阵otrain；将预报步长l作为测试步长，z1中最后的l列作为测试集的输入矩阵itest，z2中最后的l列作为测试集的输出矩阵otest；根据训练集构造的bp神经网络对测试集模拟结果的误差平方和作为其适应度值，以适应度值最小为优化方向作为评价标准评判各个粒子的优劣，记录粒子xi当前个体极值为pbest(i)，取群体中pbest(i)最优的个体作为整体极值gbest；(5)群体中的每个粒子xi，分别对其位置和速度进行更新；式中：ω为惯性权重，c1、c2为加速度因子，g为当前迭代次数，r1、r2为分布于[0,1]的随机数；(6)重新计算各个粒子此时的目标函数值，更新pbest(i)和gbest；(7)判断是否达到最大迭代次数，如满足则结束优化过程，获得经粒子群算法优化得到的参数最优值为(ibest,wbest(wbest(1),wbest(2),...,wbest(q)),lbest)，否则返回步骤(4)；(8)按ibest、wbest(wbest(1),wbest(2),...,wbest(q))、lbest构造bp神经网络训练集z3和测试集z4并初始化bp神经网络连结权值和阈值，其中：wbest(1)～wbest(i*h)为bp神经网络的输入层至隐含层神经元的连结权值的初始值，wbest(i*h+1)～wbest(i*h+h*o)为bp神经网络的隐含层至输出层神经元的连结权值的初始值，wbest(i*h+h*o+1)～wbest(i*h+h*o+h)为bp神经网络隐含层神经元的阈值的初始值，wbest(i*h+h*o+h+1)～wbest(i*h+h*o+h+o)为bp神经网络输出层神经元的阈值的初始值，就此建立起bp神经网络模型，经训练后进行迭代的l步预测，并获得对应的预测结果。s4，采用粒子群优化的rbf神经网络对残差序列的一阶差分序列进行预测，具体过程为：(1)确定需优化参数，包括：rbf神经网络输入层神经元个数i和训练集的长度l；(2)初始化种群其中q2为粒子的总数，第i个粒子为xi＝(ii,li)，粒子速度为其中ii,li为参数i、l一组备选解；(3)根据群体中的每个粒子xi(ii,li)确定的参数，构造rbf神经网络训练集的输入和输出矩阵，其中针对残差序列r及rbf神经网络输入层神经元个数ii首先建立矩阵z5和z6，其中：针对待优化神经网络训练集长度l，z5中最后的li列作为训练集的输入矩阵itrain，z6中最后的li列作为训练集的输出矩阵otrain；将预报步长l作为测试步长，z5中最后的l列作为测试集的输入矩阵itest，z6中最后的l列作为测试集的输出矩阵otest；根据训练集构造的rbf神经网络对测试集模拟结果的误差平方和作为其适应度值，以适应度值最小为优化方向作为评价标准评判各个粒子的优劣，记录粒子xi当前个体极值为pbest(i)，取群体中pbest(i)最优的个体作为整体极值gbest；(4)群体中的每个粒子xi，分别对其位置和速度进行更新；式中：ω为惯性权重，c1、c2为加速度因子，g为当前迭代次数，而r1、r2为分布于[0,1]的随机数；(5)重新计算各个粒子此时的目标函数值，更新pbest(i)和gbest；(6)判断是否达到最大迭代次数，如满足则结束优化过程，获得经粒子群算法优化得到的参数最优值为(ibest,lbest)，否则返回步骤(3)。(7)按ibest和lbest构造rbf神经网络训练集z7和测试集z8，其中：就此建立起rbf神经网络模型，经训练后进行迭代的l步预测，并获得对应的预测结果。s5，将平均电力负荷时间序列的平均值与各显著周期序列的预测结果以及残差序列的预测结果相加获得最终预测结果。实施例二按照实施例一中的步骤s1-s5，取某电网采集的小时级别的原始电力负荷时间序列，具体参见图2，由于本发明实例的目的为小时级别的短期预报，因此无需对原始电力负荷数据做任何调整就可以直接使用，即p’(i)＝p(i)，i＝1,2,...,n。本实施例中取p’(i)前1680个点为训练数据，预测其后的50个点，并以相对百分比误差mape为指标考查算法的有效性，即：其中，y(i)和p’(i)分别为电力负荷预测值和采样值，l为预测步长。图3所示为平均电力负荷时间序列的距平序列p的连续功率谱分析结果，发现该电网电力负荷序列具有12和24小时为极值点的2个显著周期带，取其极值点左右两侧各第一个低于检测线的周期点，组成周期带，此周期带为显著周期带，所述的检测线为图3中的虚线，在本实施例中，2个显著周期带分别为[21.8,26.7]和[11.4，12.6]，采用傅立叶变换fft的频域滤波的方法，提取此2个周期带对应的时间序列，分别为p1、p2，并得到对应的残差序列r，由此p＝p1+p2+r，见图4。可见，2个显著周期序列的规律性极强，可以较高精度的预测；另一方面，虽然针对残差的预测误差不可避免，但经计算，残差r的能量(方差)占比p的能量(方差)为28.56％，下降显著，因此，针对残差的预测误差要远远小于直接对于p进行预测的误差。虽然神经网络具有强大的非线性拟合能力和快速的学习能力，但如何选择恰当的神经网络模型，确定神经网络的结构、训练集和测试集仍主要靠人工经验或者试凑，其普适性较差。通过对提取的显著周期序列分析发现，虽然其具有明显的周期变化特点且序列光滑平顺，但其中序列的振幅和相位随时间细微的变化，更适合容错能力较强的bp神经网络，而残差序列经一阶差分后呈现围绕0轴波动，更适合于rbf神经网络，因此本发明实施例对提取的显著周期序列p1、p2采用基于粒子群算法优化的bp神经网络模型，而对于残差序列r则采用基于粒子群算法优化的rbf神经网络。对p1、p2采用基于粒子群算法优化的bp神经网络模型，取输入层神经元个数的范围为[5,14]，训练集的长度为[50,1650]，神经网络权值和阈值的范围为[-3,3]，粒子群种群规模是50，迭代30次。对于r则采用基于粒子群算法优化的rbf神经网络，取输入层神经元个数的范围为[5,20]，训练集的长度为[50,1650]，粒子群种群规模是50，迭代30次。表1所示为进行3步预测时，针对显著周期序列p1、p2和残差r的输入层神经元个数i和训练集长度l两个参数的优化结果，对于p1、p2建立的bp神经网络权值和阈值的优化结果由于参数过多而不一一列出。表1本实施例进行了总预测步长为50的1步、2步和3步预测实验，预测结果如图5(a)-(c)所示，表2为预测误差统计。可见，随着预测步长的增加，整体预测精度有所下降，但总体误差小于5％，预测结果较为满意。表21步预测2步预测3步预测mape0.03990.04360.0434对比实验1为了验证本发明提出的优化策略对实验结果的影响，对比实验1对原始电力负荷序列p’直接进行一次差分运算，之后建立粒子群算法优化的rbf神经网络，取输入层神经元个数的范围为[5,25]，训练集的长度为[50,1650]，粒子群种群规模是50，迭代30次。表3所示为进行3步预测时，针对原始电力负荷序列p’建立的rbf神经网络参数优化结果。表3同样的，对比实验1进行了总预测步长为50的1步、2步和3步预测实验，预测结果如图6(a)-(c)所示，表4为预测误差统计，对比表2可见，其1～3步预测的平均误差比表2增加了60.44％。表41步预测2步预测3步预测mape0.03950.07080.0933若不对p’进行一次差分运算，随意选取rbf神经网络的输入层神经元个数i和训练集长度l，最终的预测误差差异会很大，本发明实施例选取两组不同i和l对最终的预测误差的影响加以说明，如表5所示。表5两组不同参数的对比实验其1～3步预测的平均误差比表2增加了47.68％和170.61％。此组对比实验效果不好显示出神经网络参数的选择对于神经网络的学习能力和泛化造成巨大的影响，使得直接采用神经网络建模效果并不好。对比实验2针对原始电力负荷序列建立差分自回归移动平均模型(autoregressiveintegratedmovingaveragemodel，arima)模型。选取预测点前100个采样数据点，通过aic准则定阶法确定arima模型的结构，同样的，对比实验2进行了总预测步长为50的1步、2步和3步预测实验，预测结果如图7(a)-(c)所示，表6为预测误差统计，对比表2可见，其1～3步预测的平均误差比表2增加了136.25％。表61步预测2步预测3步预测mape0.01690.14860.1343综上所述：经连续功率谱分析提取的电力负荷显著周期序列规律性强，因此可以高精度的进行预测，而且显著周期序列在原序列中所占比重较大，因此奠定了较高精度预测的基础；剔除了显著周期序列后的残差序列由于在原序列中比重不大，因此预测误差相对有限。本发明所提出的将电力负荷序列经连续功率谱分析，分解为多个显著周期序列和单个残差序列，进而对各个显著周期序列和残差序列分别进行预测的方法可以大大提高整体预测效果。以上显示和描述了本发明的基本原理和主要特征和本发明的优点。本行业的技术人员应该了解，本发明不受上述实施例的限制，上述实施例和说明书中描述的只是说明本发明的原理，在不脱离本发明精神和范围的前提下，本发明还会有各种变化和改进，这些变化和改进都落入要求保护的本发明范围内。本发明要求保护范围由所附的权利要求书及其等效物界定。当前第1页12