一种基于场景法的主动配电网随机无功优化方法与流程

本发明涉及一种基于场景法的主动配电网随机无功优化方法，适用于解决考虑负荷和分布式能源接入主动配电网的不确定性时的无功优化问题。

背景技术：

随着全球经济的快速发展，世界各国的环境益恶化、能源也日渐短缺，这两大问题已成为全球性的问题。这些使得改变传统能源发展结构，不断开发利用新能源更好地促进经济、环境、性会的协调可持续发展显得十分必要。随着可再生能源技术的发展，大规模的新能源接入配电系统已经成为趋势。

主动配电网的无功优化是一种配电网的优化调度技术。以系统网损、电压等为目标函数，通过调整变压器分接头、无功补偿设备功率、分布式电源功率来实现系统的运行优化。现有无功优化方法往往没有考虑负荷和可再生能源接入导致的随机性。

技术实现要素：

发明目的：基于以上分析，本发明采用场景法，提出一种新的考虑系统随机性的主动配电网无功优化方法，并提供三种优化方案供选择，以期提高考虑负荷和新能源接入的不确定性无功优化的经济性同时保证系统安全可靠运行。

技术方案：一种基于场景法的主动配电网随机无功优化方法，用于考虑负荷以及新能源并网时主动配电网的优化调度问题。该方法按以下步骤实现：

(1)首先，建立基于场景法的随机无功优化模型，将每个场景计入优化模型。不失一般性，令x为优化后系统状态变量(电压、功率)，由于受到随机因素的影响，所以为随机变量；y为扰动变量(可再生能源、负荷)为随机变量；u为可调整控制变量；已知y概率特性，设有M个场景，其中场景i对应的概率为p_i，每个场景的扰动变量为y_i，优化后的状态变量为x_i，可得场景法优化模型如下即：

式中：u为可调整控制变量，目标函数f为网损函数，g为等值约束(潮流约束)，h为不等约束(物理运行约束和控制变量约束)。

(2)按照y的概率特性，利用蒙特卡罗法产生大量确定性场景，形成场景集合，并认为每个场景的概率均等。

(3)本发明提供三种优化方案供选择，蒙特卡罗方案，激进型场景缩减方案，保守型场景缩减方案。如果采用蒙特卡罗方案，则直接将产生场景带入优化模型，即可得到优化结果。

(4)采用激进型缩减方案，基于Kantorovich距离的场景缩减方法，其基本思路是合并场景集中距离较近的场景，通过最小化初始场景集和缩减后场景集合Kantorovich距离，使得保留场景集Ω_S能够最大程度地代表初始场景集合Ω。Kantorovich距离定义为

式中：c(i,i')为表征场景i和i'距离的函数，通常表示为c(i,i')＝||y_i-y_i'||₂。场景缩减的步骤就是每次从Ω_S中选出一个要缩减的场景，加入到Ω\Ω_S(Ω中去除Ω_S)中，为所有可选的场景D中最小。采用快速前向选择法缩减场景。将缩减后的场景集带入优化模型，即可偏激进的优化方案。

(5)采用保守型缩减方案，基于欧式距离，计算初始场景集Ω中每个场景与y的均值所构成场景之间的距离，并按距离从大到小将场景排序，根据需要选取距离最大的数个场景形成极限场景集。将极限场景集带入优化模型，即得到较为保守的无功优化方案。

附图说明

图1为本发明实施例的方法流程图；

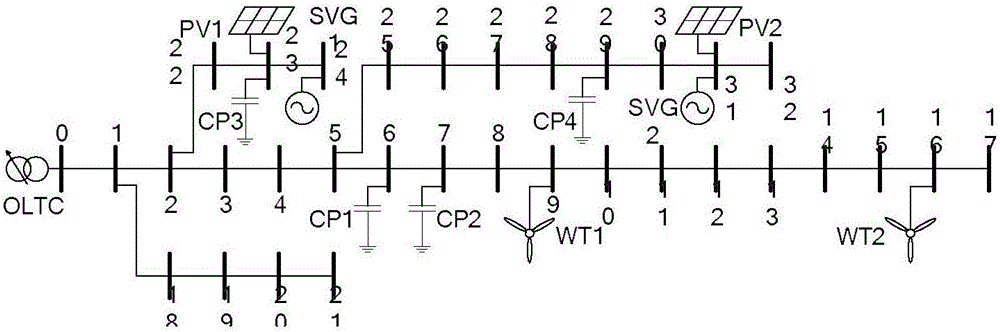
图2为修改后的IEEE33节点配点系统图；

图3为3种无功优化方案节点电压幅值期望和概率区间比较(重负荷)；

图4为3种无功优化方案节点电压幅值期望和概率区间比较(大容量DG)。

具体实施方式

下面结合具体实施例，进一步阐明本发明，应理解这些实施例仅用于说明本发明而不用于限制本发明的范围，在阅读了本发明之后，本领域技术人员对本发明的各种等价形式的修改均落于本申请所附权利要求所限定的范围。

(1)考虑负荷和新能源接入的主动配电网无功优化模型

以优化网损为目标函数虑DG的无功调控能力、可调变压器分接头位置、并联电容器投运组数、静止无功发生器(static var generator,SVG)功率为控制变量主动配电网的无功优化模型可以表示为：

式中：u是控制变量，u＝[Q_DG,T_tap,S_c,Q_SVG]，Q_DG为m个DG的无功功率向量；T_tap是可调变压器分接头位置向量，N_t为可调变压器台数；S_c为电容器组投切组数向量，Q_SVG是SVG的无功功率向量；N_L为系统支路数，R_i为支路i的电阻；P_i和Q_i分别为支路i的有功和无功功率；V_Hi为支路始端节点电压。

该最优化问题的等值约束为主动配电网功率平衡约束，不等约束为状态变量的物理运行约束和控制变量对应补偿设备的可调极限约束。

主动配电网无功优化问题可简写为：

s.t.g(x,y,u)＝0

h(x,u)≥0

式中：x为优化后系统状态变量(电压、功率)，y为扰动变量(可再生能源、负荷)，u为可调整控制变量，目标函数f为网损函数，g为等值约束(潮流约束)，h为不等约束(物理运行约束和控制变量约束)。

若考虑x受到可再生能源和负荷的不确定性影响，随机优化模型可表示为

s.t.g(x,y,u)＝0

h(x,u)≥0

式中：扰动变量y为随机变量，x为优化后系统状态变量，由于受到随机因素的影响，所以为随机变量，ρ为x的概率密度函数，u为可调整控制变量，必须为确定性变量，否则无法形成控制指令。

含随机变量的优化模型难以求解。场景法按照y的概率特性生成大量的优化前系统确定性场景，通过联立全部场景求解确定性规划，得到一优化方案u满足每一个场景的约束。不失一般性，已知y概率特性，设有M个场景，其中场景i对应的概率为p_i，每个场景的扰动变量为y_i，优化后的状态变量为x_i，可得场景法优化模型如下：

将选定的场景集带入优化模型，求解最优模型即得无功优化方案。

(2)场景缩减技术

由于优化模型中考虑了每个场景的目标函数和约束，尽管不需要迭代只需求解一次，但是优化的规模和复杂性都大大增加，并随着场景数的增加而增加。但如果使用较少场景，则较难全面考虑随机性影响而使结果偏激进。因此引入场景缩减技术场景缩减的基本原则是在保留较少场景的情况下又能充分地描述原有随机变量的分布。

本发明考虑两种场景缩减方法：激进型场景缩减方案，保守型场景缩减方案。

采用激进型缩减方案，基于Kantorovich距离的场景缩减方法，其基本思路是合并场景集中距离较近的场景，通过最小化初始场景集和缩减后场景集合Kantorovich距离，使得保留场景集Ω_S能够最大程度地代表初始场景集合Ω。Kantorovich距离定义为

式中：c(i,i')为表征场景i和i'距离的函数，通常表示为c(i,i')＝||y_i-y_i'||₂。场景缩减的步骤就是每次从Ω_S中选出一个要缩减的场景，加入到Ω\Ω_S(Ω中去除Ω_S)中，为所有可选的场景中D最小。采用快速前向选择法缩减场景。快速前向选择法步骤如下：

1)k＝0，置被删除的场景集合为空集。

2)计算第k次迭代要删除的场景i_k，删除该场景之后得到新的保留场景使得Kantorovich距离最小。

3)将i_k从中删除得到k＝k+1。

4)将被删除场景合并到中与其欧式距离最近的场景中，合并的场景概率为被删除的场景概率和合并前概率之和。

采用保守型缩减方案，基于欧式距离，计算初始场景集Ω中每个场景与y的均值所构成场景之间的距离，并按距离从大到小将场景排序，根据需要选取距离最大的数个场景形成极限场景集。将极限场景集带入优化模型，即得到较为保守的无功优化方案。

(3)三种优化方案及优化模型求解

本发明提供三种优化方案供选择，蒙特卡罗方案，激进型场景缩减方案，保守型场景缩减方案。如果采用蒙特卡罗方案，则直接将产生场景带入优化模型，即可得到优化结果；如果采用激进型缩减方案，利用基于Kantorovich距离的场景缩减方法得到大小合适的场景集，带入优化模型，可得到偏激进的优化方案；如果采用保守型缩减方案，在得到大小合适的极限场景集后，将极限场景集带入模型，即可得到偏保守的无功优化方案。

(4)下面介绍本发明的一个实施例：

如图2所示在IEEE33配电系统基础上进行修改。假设负荷服从正态分布，以系统所给负荷值作为期望，10％负荷值作为标准差。在9号、16号节点上接入最大功率为400kW的直驱式风机风电系统，逆变器最大容量为450kVA，利用非参数核密度估计得到有功功率的概率模型，数据来源于某地风电场实测功率。在23号、31号节点上接入最大功率1200kW的光伏系统，逆变器最大容量1350kVA。标幺化后的光伏有功功率服从参数为α＝0.6869、β＝2.1230的Beta分布。并加入无功补偿设备(参数如下表所示)，

表1无功补偿设备

分布式电源(DG)按如下公式计算可用调整无功功率

式中：Q_DG,max、Q_DG,min分别为无功功率上下限，S_max为逆变器最大容量，为DG有功功率P_DG的CDFF_DG(P_DG)的反函数。

利用蒙特卡罗法产生100个场景，按Kantorovich距离缩减为10个场景，并利用极限场景法后缩减为10个场景，对以上3种无功优化分别进行测试，利用粒子群算法求解优化模型。在i5四核平台MATLAB中编程，使用网损优化效果、计算时间对比测试场景法无功优化效果。同时累积概率5％到95％的概率区间，用以判断优化方案是否充分考虑随机因素的影响。考虑重负荷和大容量可再生能源接入两种情况，结果如下：

首先考虑1.8倍重负荷情况，测试结果和每个方法的方案如下表所示：

表2结果对比(负荷1.8倍)

表3无功补偿方案对比(负荷1.8倍)

画出3种形式场景法的各节点电压均值和90％概率区间如图3所示。

可看出蒙特卡罗方案能在考虑不确定性的情况下得到较好的优化结果，但计算时间偏长；基于Kantorovich距离的缩减法网损优化效果好，但是概率区间扩大，可能难以全面考虑系统的不确定性；极限场景法概率区间最为安全，但是网损优化效果差于另外两种。

然后考虑1.5倍容量DG接入情况，测试结果和每个方法的方案如下表所示：

表4结果对比(大容量DG)

表5无功补偿方案对比(大容量DG)

画出3种形式场景法的各节点电压均值和90％概率区间如图4所示，图中实心点、空心点、星号分别表示蒙特卡罗方案、激进型方案、保守型方案的节点电压均值，实线、虚线、点画线分别表示蒙特卡罗方案、激进型方案、保守型方案的90％概率区间。

所得结果与重负荷情况近似。故本发明所述方案能较好地解决考虑主动配电网不确定性的无功优化问题，如何选择方案应按实际需求决定。