适用于社交网络的基于核心三角的局部社团发现方法与流程

本发明涉及社会网络分析中的社团发现领域，具体涉及一种基于核心三角用于分析社交网络中的局部社团发现应用方法。

背景技术：

目前，社团发现研究领域的研究热点主要有社团的重叠性，局部社团发现，异构网络的社团发现，动态网络的社团发现等等。本发明着重于社团网络的局部性特征。随着社团发现研究的进展，以及现实世界中社交网络规模的不断增大，社团发现方法研究方向也逐渐向超大规模社交网络的社团发现倾斜。在信息爆炸的当代，在海量数据生成的社交网络之中，获取网络的全局结构信息变得十分困难，且通过全局的网络结构信息来生成整个网络的社团划分所需时间及计算成本变得过于高昂。而传统的应用于社交网络之上的社团发现方法通常依赖于全局网络结构信息的获取，进而难以应用于大规模社交网络，因此基于局部信息社团结构发现越来越受到重视。

所谓局部社团发现，即不依赖网络全局结构信息，基于一个初始节点或社团，通过某个节点或者边的局部信息进行扩散的方法。该类方法由于在生成一个社团时不需要获取网络的全局结构信息，大大加快了社团生成的速度。社交网络规模通常非常庞大，获取全局网络的社团划分通常成本较高且没有必要，基于单个用户的社团结构分析往往更具有实用价值。

技术实现要素：

本发明即针对社交网络的社团发现问题提出了一种解决方案，即适用于社交网络的基于核心三角的局部社团发现方法。

具体技术方案如下：适用于社交网络的基于核心三角的局部社团发现方法包括如下步骤：

1)核心三角选取阶段：

a确定核心节点；

b找到核心节点与其邻居节点构成的所有三角形；

c选取度数最高的作为核心三角；

d结束；

2)局部社团扩张阶段：

a核心三角作为初始社团；

b计算每个社团邻居节点的节点适应度；

c选取节点适应度最大的邻居节点加入社团迭代生成局部社团；

d结束；

3)局部社团合并阶段：

a计算两局部社团之间相似度；

b基于相似度阈值两两合并局部社团；

c结束。

本发明中，步骤1)-a中所述核心节点由使用者自行确定。

本发明中，步骤1)-b中所述的三角形由以下公式定义：

t＝δ{va|(vb，vc)∈a}

其中a是节点va的所有邻居节点集合，vb、vc是集合a中的节点。

本发明中，2)-b中所述节点适应度的定义如下：

对于当前局部社团，社团适应度由以下公式定义：

其中，α∈(0，1]为一个用以控制社团规模大小的参数。为局部社团内部的边度数，公式中为局部社团外部的边度数；

根据以上局部社团适应度fg的定义，可以给出一个不属于社团g的节点v的节点适应度，即将节点v加入局部社团后，局部社团g的适应度的增量：

其中，fg+v表示加入了节点v后的局部社团的适应度，fg+v与fg的差值即是节点v对局部社团g的适应度的贡献度

本发明中，步骤3)-b中所述两局部社团之间相似度由以下公式定义：

其中ci∩cj为社团ci和cj中共有节点总数，min(ci，cj)为ci和cj两者中节点数最少的数值。制定参数∈，若两社团间相似度将其合并为一个社团。

本发明的有益效果：本发明的一种适用于社交网络的基于核心三角的局部社团发现方法，通过核心三角寻找，局部社团扩张等阶段，能够有效地生成社交网络中局部社团结构划分。有效解决了基于全局网络结构信息的社团发现方法计算效率低的问题。

附图说明

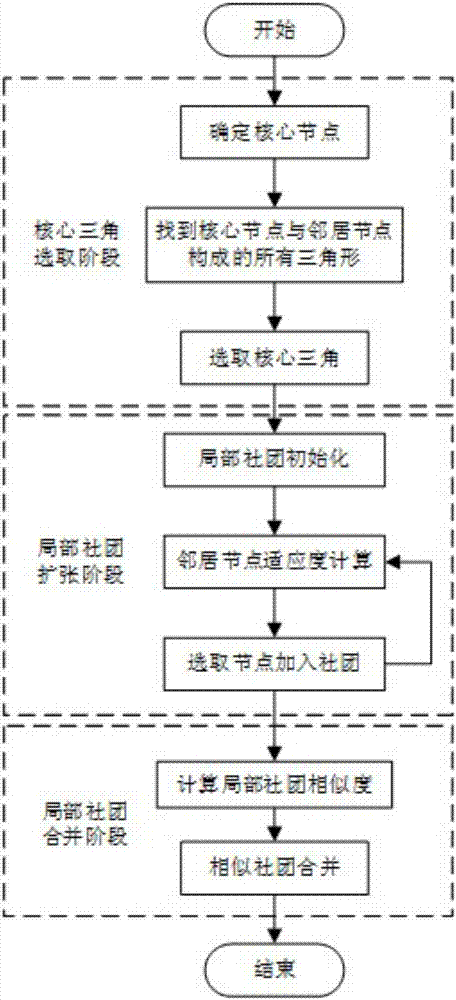
图1为适用于社交网络的基于核心三角的局部社团发现方法的流程图。

图2为选取核心三角的流程图。

图3为基于核心三角扩张生成一个局部社团的流程图。

具体实施方式

为了更了解本发明的技术内容，特举具体实施例并配合所附图式说明如下。

如图1为本发明实施适用于社交网络的基于核心三角的局部社团发现方法的流程图，具体步骤描述如下：

步骤1-0是该流程的开始；

步骤1-1是确定核心节点；

步骤1-2是找到核心节点与其邻居节点构成的所有三角形，三角形由以下公式定义：

t＝δ{va|(vb，vc)∈a}

其中a是节点va的所有邻居节点集合，vb、vc是集合a中的节点；

步骤1-3是选取度数最高的作为核心三角；

步骤1-4是基于核心三角初始化局部社团；

步骤1-5是计算局部社团所有邻居节点的适应度；

步骤1-6是选取适应度最高的节点加入到局部社团当中；

步骤1-7是计算两两局部社团之间的相似度，具体相似度公式如下：

步骤1-8是若两社团的相似度大于一定的阈值∈，则两社团相似，将两社团合并为一个社团，该过程迭代进行，直至所有局部社团之间都不相似为止，设定阈值参数∈为0.7；

步骤1-9是该流程的结束。

如图2所示，本发明在核心三角选取阶段的方法流程图，具体步骤描述如下：

步骤2-0是该流程的开始；

步骤2-1是选取核心节点a，并初始化核心三角集合t，初始值为空；

步骤2-2是分别遍历节点a的邻居节点b和c；

步骤2-3是判断是否遍历过所有的邻居节点，若遍历结束，跳转到步骤2-7；过没有遍历结束，继续步骤2-4；

步骤2-4是判断节点a，b，c是否能够构成一个三角形t，若不能构成三角形，跳转到步骤2-2；若能够构成一个三角形，继续步骤2-5；

步骤2-5是判断由节点a，b，c构成的三角形t的度数总和是否大于集合t的度数总和，若不大于，跳转到步骤2-2；若大于，继续步骤2-6；

步骤2-6是更新集合t，先清空集合t，并将节点a，b，c加入到集合t中，并跳转到步骤2-2；

步骤2-7是该流程的结束；

如图3所示，本发明在局部社团扩张阶段的方法流程图，具体步骤描述如下：

步骤2-0是该流程的开始；

步骤3-1是基于核心三角初始化局部社团d，并初始化该局部社团的邻居节点集和s；

步骤3-2是计算集合s中所有节点的节点适应度，具体计算方法如下：

1)使用如下公式计算当前社团的适应度：

2)使用如下计算当前社团加入节点v的适应度增量：

步骤3-3是判断是否集合s中所有节点适应度皆小于0，若都小于0，跳转到步骤3-6；若不是，继续步骤3-4；

步骤3-4是选取集合s中适应度最高的节点加入当前社团；

步骤3-5是更新节点集合d，s，将适应度最高的节点加入d，并将新的与d邻接且不属于d的节点加入s，并跳转到步骤3-2；

步骤3-6是流程的结束，输出局部社团划分的集合d。

综上所述，本发明的一种适用于社交网络的基于核心三角的局部社团发现方法，通过核心三角寻找，局部社团扩张等阶段，能够有效地生成社交网络中局部社团结构划分。有效解决了基于全局网络结构信息的社团发现方法计算效率低的问题。

虽然本发明已以较佳实施例揭露如上，然其并非用以限定本发明。本发明所属技术领域中具有通常知识者，在不脱离本发明的精神和范围内，当可作各种的更动与润饰。因此，本发明的保护范围当视权利要求书所界定者为准。