一种骨折复位的计算机辅助设计方法与流程

本发明涉及计算机手术导航领域，具体涉及一种骨折复位的计算机辅助设计方法。

背景技术：

骨折是指骨结构的连续性完全或部分断裂，是和人们生活有密切关系的常见创伤。骨折患者的正常解剖结构被破坏，影响了肢体功能，降低生活质量，给社会和家庭带来了负担。随着现代影像技术的不断发展，x线、计算机体层摄影(ct)、核磁共振成像能将绝大多数骨折明确诊断，清晰的显示骨折类型和移位情况等，指导临床治疗。ct扫描获取的医学图像能清楚反映复杂关节内和脊柱等骨折的详细信息，重建的三维图像能够更便捷地指导外科手术治疗方案，在临床上得到了广泛应用。

多数移位的骨折患者需要行骨折复位手术治疗。手术过程中，骨科医师依赖x线透视明确骨折断端位置、复位情况和内固定物的置入位置等，而过程中的射线暴露对患者和医师造成潜在的风险。目前常用的术中透视设备多为c形臂和g形臂，获取的图像为二维图像，骨科医师需结合临床经验判断骨折复位情况，手术操作难度大，因此需发展新的手术导航系统解决上述问题。

技术实现要素：

为实现在减少射线透视次数的同时保证骨折断端信息的充分性与准确性，本发明提出了一种骨折复位的计算机辅助设计方法，利用计算机模拟给出骨折复位的最优路径，进而辅助医生操作，为医生操作带来便利的同时也能在一定程度上促进数字时代的医疗卫生发展。

本发明的一种骨折复位的计算机辅助设计方法，包括以下步骤：

1)通过ct扫描图像重建出两块骨折断端的三维的刚体点系模型，并确定两块骨折断端的髓腔内壁和骨外壁的空间刚体点系；

2)利用主成分分析(principalcomponentanalysis，pca)方法分别确定两块骨折断端的断截面的长短主轴，以此为基础给出各自对应的三维直角坐标系，并确定骨折断端的中心主轴；

3)判断两块骨折断端的可移动度，远心端骨折断端为可移动度大的骨折断端，将其作为可移动的骨折断端，近心端骨折断端为可移动度小的骨折断端，以近心端骨折断端为参照，向近心端骨折断端转动远心端骨折断端，实现两块骨折断端的共轴；

4)两块骨折断端共轴后，确定两断截面的断截面方程，确定远心端骨折断端的旋转角度，达到两个断截面的长主轴和短主轴均重合；

5)沿中心主轴无旋转的平移远心端骨折断端，实现两块骨折断端的完全复位，完成骨折复位的最优路径设计。

其中，在步骤2)中，利用主成分分析pca方法分别确定两块骨折断端的断截面的长主轴和短主轴，并以此为基础给出各自对应的三维直角坐标系中的x1o1y1平面和x2o2y2平面；长主轴与短主轴的交点为断截面的中心点，也是三维直角坐标系中的原点o1和o2，将过o1点且垂直于x1o1y1平面的轴作为三维直角坐标系中的z1轴，同理将过o2点且垂直于x2o2y2平面的轴作为三维直角坐标系中的z2轴，并设定由断截面指向骨折断端外部的方向为正方向；确定平行于骨外壁且经过断截面中心点的直线，将其作为骨折断端的中心主轴，骨折断端的中心主轴与其各自的z轴之间的夹角为θ，θ≥0。

在步骤3)中，通过与心脏间的距离大小判断两块骨折断端的可移动度。以近心端骨折断端为参照，向近心端骨折断端移动远心端骨折断端，具体包括以下步骤：分别取在两块骨折断端各自的中心主轴方向上的矢量，并给出矢量在三维直角坐标系中的四元数表示，其中对于远心端骨折断端，转动前其中心主轴方向的矢量表示为r1＝(m1,m2,m3)，近心端骨折断端的中心主轴方向的矢量表示为恒定的r2＝(n1,n2,n3)；将r1＝(m1,m2,m3)与r2＝(n1,n2,n3)作为转动过程中的初始姿态与终止姿态，通过四元数球面线性插值的方法得到转动过程中姿态变换的空间位置表示，实现两块骨折断端的中心主轴的共轴。

在步骤4)中，确定两断截面的断截面方程，确定远心端骨折断端的旋转角度，达到两个断截面的长主轴和短主轴均重合，具体包括以下步骤：远心端骨折断端和近心端骨折断端的三维直角坐标系分别表示为c1(x1,y1,z1)和c2(x2,y2,z2)，进一步由断截面的中心点与共同的中心主轴分别确定两断截面的断截面方程，其中远心端骨折断端的断截面方程表示为π1:a1x1+b1y1+c1z1＝0，近心端骨折断端的断截面方程表示为π2:a2x2+b2y2+c2z2＝0，且确定该截面对应的法向量为h，以向量h作为远心端骨折断端的截面方程的法向量并结合满足方程π2的一个点，给出两断截面法向量平行时的远心端骨折断端的断截面方程π3:a3x1+b3y1+c3z1＝0，通过与方程π1的对比确定远心端骨折断端的旋转角度，达到两个断截面的长短主轴均重合。

在步骤5)中，沿中心主轴无旋转的平移远心端骨折断端，具体包括以下步骤：确定两块骨折断端共同的中心主轴与其各自断截面的交点分别为p1和p2，以远心端骨折断端的截面中的p1点为起点得到两点间的矢量l并沿中心主轴无旋转的平移远心端骨折断端，实现两块骨折断端的完全复位，完成骨折复位的最优路径设计。

本发明的优点：

本发明确定骨折断端的断截面长短主轴、建立三维直角坐标系、确定中心主轴及其方向上的矢量在三维坐标系中的四元数表示、选定易操作的骨折断端作为远心端骨折断端、分别进行转动、自旋和平移的操作得到骨折断端共轴最优路径点，完成骨折复位；本发明应用四元数表示两块骨折断端的中心主轴方向的矢量，进而得到每次转动的转轴与转动角度，四元数相对于欧拉角、旋转矩阵等方法，在描述旋转变换时求解速度更快，并可有效避免万向锁等问题的出现；本发明通过对骨折断端进行旋转、自旋和平移操作，得到最优的骨折断端共轴轨迹点，可为医生诊断与操作提供有效信息。

附图说明

图1为本发明的骨折复位的计算机辅助设计方法的流程图；

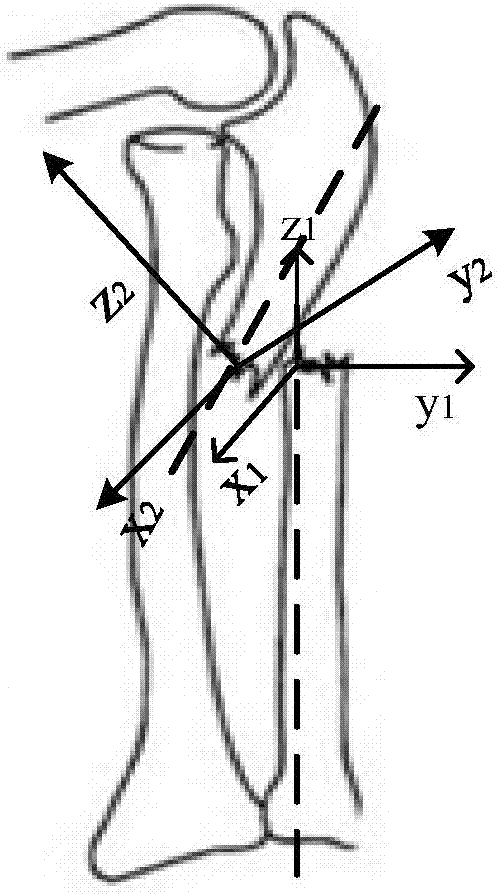
图2为本发明的骨折复位的计算机辅助设计方法的断截面建立的三维直角坐标系与中心轴线的示意图。

具体实施方式

下面结合附图，通过具体实施例，进一步阐述本发明。

如图1所示，本实施例的骨折复位的计算机辅助设计方法，包括以下步骤：

1)通过ct扫描图像重建出两块骨折断端的三维的刚体点系模型，并确定两块骨折断端的髓腔内壁和骨外壁的空间刚体点系；

2)利用主成分分析(principalcomponentanalysis，pca)方法分别确定两块骨折断端的断截面的长短主轴，并以此为基础给出各自对应的三维直角坐标系中的x1o1y1平面和x2o2y2平面；长主轴与短主轴的交点为断截面的中心点，也是三维直角坐标系中的原点o1和o2，将过o1点且垂直于x1o1y1平面的轴作为三维直角坐标系中的z1轴，同理将过o2点且垂直于x2o2y2平面的轴作为三维直角坐标系中的z2轴，并设定由断截面指向骨折断端外部的方向为正方向；确定平行于骨外壁且经过断截面中心点的直线，将其作为骨折断端的中心主轴，骨折断端的中心主轴与其各自的z轴之间的夹角为θ，θ≥0；

3)通过与心脏间的距离大小判断两块骨折断端的可移动度，可移动度大的骨折断端为远心端骨折断端，作为可移动的骨折断端，可移动度小的骨折断端为近心端骨折断端，以近心端骨折断端为参照，向近心端骨折断端移动远心端骨折断端；分别取在两块骨折断端各自的中心主轴方向上的矢量，并给出矢量在三维直角坐标系中的四元数表示，其中对于远心端骨折断端，转动前其中心主轴方向的矢量表示为r1＝(m1,m2,m3)，近心端骨折断端的中心主轴方向的矢量表示为恒定的r2＝(n1,n2,n3)；将r1＝(m1,m2,m3)与r2＝(n1,n2,n3)作为转动过程中的初始姿态与终止姿态，通过四元数球面线性插值的方法得到转动过程中姿态变换的空间位置表示，实现两块骨折断端的中心主轴的共轴；

4)两块骨折断端共轴后，其三维直角坐标系分别表示为c1(x1,y1,z1)和c2(x2,y2,z2)，进一步由断截面的中心点与共同的中心主轴分别确定两断截面的断截面方程，其中远心端骨折断端的断截面方程表示为π1:a1x1+b1y1+c1z1＝0，近心端骨折断端的断截面方程表示为π2:a2x2+b2y2+c2z2＝0，且确定该截面对应的法向量为h，以向量h作为远心端骨折断端的截面方程的法向量并结合满足方程π2的一个点，给出两断截面法向量平行时的远心端骨折断端的断截面方程π3:a3x1+b3y1+c3z1＝0，通过与方程π1的对比确定远心端骨折断端的旋转角度，达到两个断截面的长短主轴均重合；

5)确定两块骨折断端共同的中心主轴与其各自断截面的交点分别为p1和p2，以远心端骨折断端的截面中的p1点为起点得到两点间的矢量l并沿中心主轴无旋转的平移远心端骨折断端，实现两块骨折断端的完全复位，完成骨折复位的最优路径设计。

最后需要注意的是，公布实施例的目的在于帮助进一步理解本发明，但是本领域的技术人员可以理解：在不脱离本发明及所附的权利要求的精神和范围内，各种替换和修改都是可能的。因此，本发明不应局限于实施例所公开的内容，本发明要求保护的范围以权利要求书界定的范围为准。