一种基于像差理论确定二次曲面非球面度的方法与流程

本发明属于先进光学制造技术领域，具体涉及一种基于像差理论确定二次曲面非球面度的方法。

背景技术：

由于非球面比球面可以提供更大的自由度，所以在光学系统中使用非球面可以缩小系统整体外形尺寸，减轻系统重量，改善成像质量等优点。

无论是基于确定性数控技术的先进光学制造还是传统的光学冷加工都需要知道非球面加工时的去除函数。非球面的加工一般都是从最接近比较球面开始的，比较球面与非球面之间的偏差定义为非球面度，一般作为非球面加工时的材料去除函数。全口径非球面可以看做内环孔径为零的环形孔径非球面。环形孔径二次曲面最接近比较球面是指比较球面与环形孔径二次曲面内、外边缘相接触，且比较球面的球心在二次曲面的对称轴上。

潘君骅院士在《光学非球面的设计、加工与检测》一文中(苏州大学出版社2014年12月第一版第62-65页)，分别对全口径和环形孔径非球面的非球面度的计算做了一些说明，但并没有给出具体的非球面度计算的表达式。后来刘慧兰、沙定国、王权陡、鄢定尧、韦资华、杜玉军、陆永贵、谢枫、李俊峰等都对非球面度的计算进行过研究，基本都是采用代数、几何和矩阵的方法，计算过程比较复杂，更是没有将全口径和环形孔径非球面的非球面度的计算统一起来，用统一的方程式进行表达。

技术实现要素：

发明目的：为了解决现有技术的不足，本发明提供了一种基于像差理论确定二次曲面非球面度的方法。

技术方案：一种基于像差理论确定二次曲面非球面度的方法，包括如下步骤：

步骤一、依据物点在二次曲面顶点曲率中心时的波像差方程建立环形孔径二次曲面的波像差方程；

步骤二、利用环形孔径非球面最接近比较球面特征，确定最接近比较球面曲率中心与非球面顶点曲率中心的偏移量并代入环形孔径二次曲面的波像差表达式，得到仅含有环形孔径二次曲面参数的波像差表达式w(y)，最后利用非球面度δ(y)与波像差之间的关系δ(y)＝0.5w(y)即可确定非球面度表达式，全口径非球面可以看做内环孔径为零的环形孔径非球面，环形孔径非球面的最接近比较球面是指比较球面与环形孔径非球面内、外边缘相接触，且比较球面的球心在二次曲面的对称轴上。

作为优化：环形孔径二次曲面的非球面度表达式为：

式中k为二次曲面常数，r0二次曲面顶点曲率半径，ɑ为遮拦比，即环形孔径二次曲面内、外环孔径之比；

当遮拦比ɑ＝0时，环形孔径二次曲面演变为全口径二次曲面，环形孔径二次曲面的结果适用于全口径非球面，其非球面度表达式为

有益效果：本发明可直观、快速地确定二次曲面加工时材料去除函数。该方法将全口径、环形孔径非球面的非球面度的计算统一起来，理论可靠，表达式简单，能够显著提高工作效率。

附图说明

下面结合附图和实例对本发明作进一步说明。

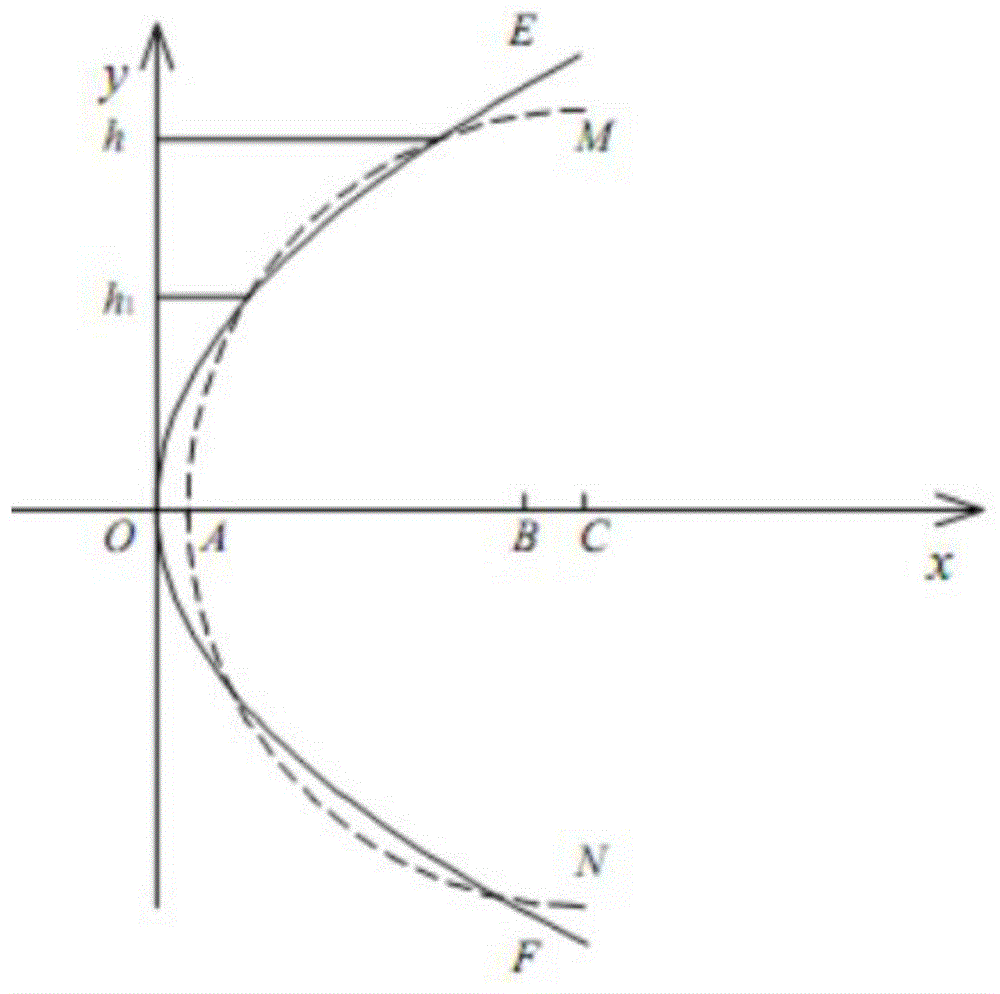
图1为环形孔径二次曲面及其最接近比较球面示意图；

图2为全口径二次曲面非球面度曲线；

图3为环形孔径二次曲面非球面度曲线。

具体实施方式

下面将对本发明实施例中的技术方案进行清楚、完整地描述，以使本领域的技术人员能够更好的理解本发明的优点和特征，从而对本发明的保护范围做出更为清楚的界定。本发明所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例，基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例，都属于本发明保护的范围。

实施例

环形孔径二次曲面最接近比较球面是指比较球面与环形孔径二次曲面内、外边缘相接触，且比较球面的球心在二次曲面的对称轴上，如图1所示。图中曲线eof为二次曲面的子午截线，曲线man为二次曲面最接近比较球面的子午截线，ox为对称轴。o为二次曲面子午截线的顶点与对称轴的交点，a为最接近比较球面的子午截线与对称轴的交点，b二次曲面子午截线顶点曲率半径的圆心，c为最接近比较球面子午截线的圆心，h1＝d1/2，h＝d/2，d1，d分别为非球面内、外环的孔径。

一般情况下非球面采用其子午截线的方程表示即可，方程式为：

式中，c为非球面顶点曲率，k为二次曲面常数，a1，a2为高次项系数，y为纵坐标，表示非球面的半口径坐标，x为横坐标，表示非球面的矢高。

实际应用中，在求解非球面度时，通常忽略非球面的高次项，仅按二次曲面进行计算。

基于波像差理论，参考专利(cn201410324768.4“一种判断旋转轴对称非球面能否采用直接干涉检测的方法”)，对于环形孔径非球面的波像差表达式，可写为，

当内边缘和外边缘波像差相等时可知：

所以此时的离焦量δ为：

此时的波像差方程为，

为了书写方便，令h1＝αh，α称为遮拦比。方程式(5)改写为：

由δ(y)＝0.5w(y)可知：

二次曲面一般分为全口径二次曲面、环形孔径二次曲面以及离轴二次曲面。离轴二次曲面可以看作是环形孔径二次曲面的一部分。全口径二次曲面可以看作是内环孔径为0的环形孔径二次曲面。当ɑ＝0时，

当dδ/dy＝0时，非球面度取极值，由方程式(8)可得：

所以，

方程式(10)中y为中性带的位置。方程式(11)中δmax为最大非球面度，a＝d/f’为非球面的相对孔径。方程式(10)、(11)与潘君骅院士著作《光学非球面的设计、加工与检测》中的结果是一致的。二次曲面既可以是凹面，也可以是凸面；当二次曲面为凹面时r0为负值，当二次曲面为凸面时r0为正值。

图2为某全口径凹二次曲面非球面度曲线，其参数为：r0＝-1440毫米，k＝-1.00486，d＝2h＝600毫米。将参数带入方程式(9)，即可快速得到非球面度表达式为

图3为某环形孔径凹二次曲面非球面度曲线，其参数为：r0＝-1440毫米，k＝-1.00486，内环口径d1＝2h1＝300毫米，外环口径d＝2h＝600毫米。将参数带入方程式(7)，即可快速得到非球面度表达式为

本发明提供了一种基于像差理论确定二次曲面非球面度的方法，简化了非球面度的计算过程，且表达式中各参数仅与非球面自身参数有关；从结果看，本发明得到的结果与传统方法得到的结果一致，说明本发明的计算方法是准确的、可靠的。