一种自动化装配位姿态测量方法与流程

本发明涉及自动化装配技术领域，尤其涉及一种自动化装配位姿态测量方法。

背景技术：

机器人抓取四种类型的半球形回转体(包含部分圆柱段)产品进行装配，在装配过程中对产品进行位置测量和监测，主要包括回转轴线位姿测量、圆周方位测量、穿管监测及装配间隙测量。

对于错位量测量，由于半球形回转体可能不存在孔洞，无法以特征标记点进行定位，用视觉3d定位测量精度只能做到0.1mm,将不能保证本任务测量精度。

技术实现要素：

本发明的目的是为了解决现有技术中存在的缺点，而提出的一种精度较高、使用方便的自动化装配位姿态测量方法。

为了实现上述目的，本发明采用了如下技术方案：一种自动化装配位姿态测量方法，包括如下步骤：

步骤一：装配产品a和产品b：

机器人抓取产品b到待装配位置，此位置记为位置1；

机器人抓取产品b竖直下向运动，使产品b的大孔与产品a圆柱头进行装配，此位置记为位置2；

产品b下降至产品a上方5mm处，此时φ3mm细管与φ25mm大孔理论同轴，此位置记为位置3；

产品a旋转约24°使φ3mm细管旋入r2mm半孔，使φ3mm细管与r2mm半孔同轴，并保证间隙均匀不发生干涉，此位置记为位置4；

产品b继续下降5mm,使下端面贴合，装配完毕，此位置记为位置5；

步骤二：对产品进行位姿测量和产品错位量测量：

在位置1对产品b的圆柱曲线进行测量，分上下两段，计算产品b的空间位姿；

在位置5通过测量产品a、b的圆柱曲线，拟合圆心，进行横向错位量测量。

进一步的，所述产品a为不锈钢材质，产品直径约φ250mm,表面粗糙度ra0.8-1.6,固定在可旋转托座上，回转精度0.01°；顶端距中心轴线30mm处有φ3细管，细管长度约200mm,平行度小于φ0.2mm,细管头部有40mm长φ23圆柱头；产品圆周方向有10mm宽3mm深沟槽与0.2mm宽刻线。

进一步的，所述产品b为粉末压铸材质，表面粗糙度ra1.6-3.2,由机器人抓取对产品a进行套装，直径约φ300mm,高度约250mm,壁厚约25mm；产品顶端距中心轴线30mm处有竖直φ25mm大孔，大孔边缘有r2mm半孔，半孔中心距产品中心轴线为30mm；产品圆周方向也有10mm宽3mm深沟槽与0.2mm宽刻线。

进一步的，所述位姿测量包括：

利用2台二维激光轮廓扫描仪，测量产品b到扫描仪的距离，形成2组以到圆柱面为x,激光线坐标y的点集；2个点集拟合成的圆心构建成圆柱体的中心线，位姿测量精度≤0.01°，位置测量精度≤0.01mm。

进一步的，所述位姿测量采用二维激光传感器。

进一步的，所述产品错位量测量包括：

在位置5，利用2台二维激光轮廓扫描仪，测量扫描仪到产品b、产品a的距离，形成2组以到圆柱面位移为z,激光线坐标x的点集，以2个点集拟合成的圆心坐标相减，得到圆心距即为产品a与产品b的横向错位量，错位测量精度≤0.01mm。

进一步的，对产品a和产品b的空间位姿及横向错位量进行实验验证，验证软件是否能够对产品位置数据进行准确的定量分析，获得位姿角度及圆周错位量数据，与人工检测结果相比，角度差异应小于10％；合格范围0.01mm，单次检测时间应小于15s。

进一步的，以人工装配或机器人装配进行实验验证，能够对产品a和产品b多次检测的数据进行对比分析，以报表的形式实现检测数据的显示，并可按照产品装配过程进行数据存储，存储量小于500m。

本发明的有益效果为：

(1)本发明提供的一种自动化装配位姿态测量方法，采用2个激光轮廓传感器，成90°夹角安装，在测量时通过升降平台上升至位置1进行数据采集测量，测量系统同时获取2个激光传感器的点阵数据，激光传感器在产品b下端测得的点阵数据经数据处理成圆周坐标，即为产品b的圆周曲线坐标，通过椭圆拟合得到第1个圆心坐标(x1,y1)；激光传感器随升降平台上移一段距离f1，获取2个激光传感器数据，拟合得到第2个圆心坐标(x2,y2)，则得到三维空间的两个点(x1,y1,0),(x2,y2,f1),两点的连线即为产品b的中心轴线，依此计算出其偏转角度及位置，本发明具有使用方便，便于测量，精度较高的优点。

附图说明

图1为本发明提出的位姿测量的示意图；

图2为本发明提出的位姿测量的流程图；

图3为本发明提出的错位测量的示意图；

图4为本发明提出的错位测量的计算流程图；

图5为本发明最小二乘法的推导算法模型图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

除非另有定义，本文所使用的所有的技术和科学术语与属于本发明的技术领域的技术人员通常理解的含义相同。本文中在本发明的说明书中所使用的术语只是为了描述具体的实施例的目的，不是旨在于限制本发明。本文所使用的术语“及/或”包括一个或多个相关的所列项目的任意的和所有的组合。

本发明采用的传感器为德国米铱cancontrol2900紧凑型系列激光轮廓扫描传感器，在静态和动态测量任务中都表现良好。传感器的轮廓频率可高达200hz和128，000测量点/秒。scancontrol2900-25高速系列传感器可以满足高速及3d应用需要。x-轴线性量程可至29.1mm，x-轴分辨率1280测量点/每轮廓(即22.7μm)，传感器的轮廓频率可达4,000hz和2,560,000测量点/秒。扫描探头可以通过以太网供电，可以仅用一根电缆同时满足数据传输和供电，减少电缆布线。全部电路都集成在传感器探头内，因此减少了电缆布线，从而方便了机械集成和基于机械手的应用。z轴检测精度可达2μm。激光传感器外形尺寸96x85x33mm

或

博智慧达hd6-0020系列激光传感器，波长为405nm的短波长激光，采用激光三角反射式原理，实现物体任一轮廓尺寸测量，如高度差、宽度、角度、半径等，也可实现缺陷检测、外观尺寸扫描、表面特征跟踪等功能。激光器采用1280测量点每扫描线，x轴分辨率21um(即相邻测量点间距距离),z轴测量重复精度2um；可检测玻璃和高反光材料，可进行轮廓传输或测量数据输出，适用于机器人应用。

曲线拟合、角度计算等功能采用halcon图像分析软件进行处理。

数据报表、数据存储压缩采用visualstudio开发。

本发明中的测量算法模块采用opencv、c++开发。其中opencv对二维激光轮廓仪采集的离散点数据进行噪声处理，剔除数据中的部分无效点；对于中心拟合采用改进的最小二乘法圆拟合。opencv是一个基于bsd许可(开源)发行的跨平台计算机视觉库，可以运行在linux、windows、android和macos操作系统上。它轻量级而且高效——由一系列c函数和少量c++类构成，同时提供了python、ruby、matlab等语言的接口，实现了图像处理和计算机视觉方面的很多通用算法。

opencv用c++语言编写，它的主要接口也是c++语言，但是依然保留了大量的c语言接口。该库也有大量的python、javaandmatlab/octave(版本2.5)的接口。这些语言的api接口函数可以通过在线文档获得。如今也提供对于c#、ch、ruby,go的支持。

最小二乘法是用最简的方法求得一些绝对不可知的真值，而令误差平方之和为最小来寻找一组数据的最佳匹配函数的计算方法，最小二乘法通常用于曲线拟合(leastsquaresfitting)。最小二乘圆拟合方法是一种基于统计的检测方法，即便是图像中圆形目标受光照强度不均等因素的影响而产生边缘缺失，也不会影响圆心的定位和半径的检测，若边缘定位精确，最小二乘法可实现高精度级别的精确拟合定位。

如图5，最小二乘法的推导方法如下：

最小二乘法拟合圆曲线：r²＝(x-a)²+(y-b)²

r²＝x²-2ax+a²+y²-2by+b²

令

a＝-2a

b＝-2b

c＝a²+b²-r²

可得圆曲线方程的另一个形式：

x²+y²+ax+by+c＝0(1)

只要求出参数a，b，c就可以求得圆心半径的参数：

样本集(xi，yi)i∈(1，2，3...n)中点到圆心的距离为di；

di²＝(xi-a)²+(yi-b)²

点(xi，yi)到圆边缘的距离的平方与和半径平方的差为：

δi＝di²-r²＝(xi-a)²+(yi-b)²-r²＝xi²+yi²+axi+byi+c

令q(a，b，c)为δi的平方和；

q(a，b，c)＝∑δi²＝∑[(xi²+yi²+axi+byi+c)]²

求参数a，b，c使得q(a，b，c)的值最小值。

解：

平方差q(a，b，c)大干0，因此函数存在大于或等于0的极小值，极大值为无穷大。

f(a，b，c)对a，b，c求偏导，令偏导等于0，得到极值点，比较所有极值点的函数值即可得到最小值。

解这个方程组。

先消去c

(2)*n-(4)*∑xi得：

n∑(xi²+yi²+axi+byi+c)xi-∑(xi²+yi²+axi+byi+c)×∑xi＝0

n∑(xi²+yi²+axi+byi)xi-∑(xi²+yi²+axi+byi)×∑xi＝0

(3)*n-(4)*∑yi得：

n∑(xi²+yi²+axi+byi+c)yi-∑(xi²+yi²+axi+byi+c)×∑yi＝0

n∑(xi²+yi²+axi+byi)y-∑(xi²+yi²+axi+byi)×∑yi＝0

令

c＝(n∑xi²-∑xi∑xi)

d＝(n∑xiyi-∑xi∑yi)

e＝n∑xi³+n∑xiyi²-∑(xi²+yi²)∑xi

g＝(n∑yi²-∑yi∑yi)

h＝n∑xi²yi+n∑yi³-∑(xi²+yi²)∑yi

可解得：

ca+db+e＝0

da+gb+h＝0

得a、b、r的估计拟合值：

传统的最小二乘法对样本数据中非均匀分布噪声比较敏感，对于均匀分布的噪声可以很精确。

一种自动化装配位姿态测量方法，包括如下步骤：

步骤一：装配产品a和产品b：

机器人抓取产品b到待装配位置，此位置记为位置1；

机器人抓取产品b竖直下向运动，使产品b的大孔与产品a圆柱头进行装配，此位置记为位置2；

产品b下降至产品a上方5mm处。此时φ3mm细管与φ25mm大孔理论同轴，此位置记为位置3；

产品a旋转约24°使φ3mm细管旋入r2mm半孔，使φ3mm细管与r2mm半孔同轴，并保证间隙均匀不发生干涉，此位置记为位置4；

产品b继续下降5mm,使下端面贴合，装配完毕，此位置记为位置5；

步骤二：对产品进行位姿测量和产品错位量测量：

在位置1对产品b的圆柱曲线进行测量，分上下两段，计算产品b的空间位姿；

在位置5通过测量产品a、b的圆柱曲线，拟合圆心，进行横向错位量测量。

进一步的，所述产品a为不锈钢材质，产品直径约φ250mm,表面粗糙度ra0.8-1.6,固定在可旋转托座上，回转精度0.01°；顶端距中心轴线30mm处有φ3细管，细管长度约200mm,平行度小于φ0.2mm,细管头部有40mm长φ23圆柱头；产品圆周方向有10mm宽3mm深沟槽与0.2mm宽刻线。

进一步的，所述产品b为粉末压铸材质，表面粗糙度ra1.6-3.2,由机器人抓取对产品a进行套装，直径约φ300mm,高度约250mm,壁厚约25mm；产品顶端距中心轴线30mm处有竖直φ25mm大孔，大孔边缘有r2mm半孔，半孔中心距产品中心轴线为30mm；产品圆周方向也有10mm宽3mm深沟槽与0.2mm宽刻线。

进一步的，所述位姿测量包括：

利用2台二维激光轮廓扫描仪，测量产品b到扫描仪的距离，形成2组以到圆柱面为x,激光线坐标y的点集；2个点集拟合成的圆心构建成圆柱体的中心线。位姿测量精度≤0.01°，位置测量精度≤0.01mm。

进一步的，所述位姿测量采用二维激光传感器。

进一步的，所述产品错位量测量包括：

在位置5，利用2台二维激光轮廓扫描仪，测量扫描仪到产品b、产品a的距离，形成2组以到圆柱面位移为z,激光线坐标x的点集，以2个点集拟合成的圆心坐标相减，得到圆心距即为产品a与产品b的横向错位量，错位测量精度≤0.01mm。

进一步的，对产品a和产品b的空间位姿及横向错位量进行实验验证，验证软件是否能够对产品位置数据进行准确的定量分析，获得位姿角度及圆周错位量数据，与人工检测结果相比，角度差异应小于10％；合格范围0.01mm。单次检测时间应小于15s。

进一步的，以人工装配或机器人装配进行实验验证，能够对产品a和产品b多次检测的数据进行对比分析，以报表的形式实现检测数据的显示，并可按照产品装配过程进行数据存储，存储量小于500m。

实施例1：

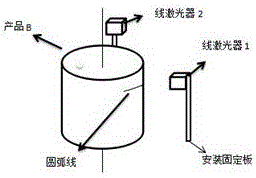
如图1-图2所示：

位姿测量：

半球型产品b在装配位置1时，竖直方向上可看作一个圆柱体，在水平方向上通过测取2条圆柱体表面圆周曲线，进行圆拟合；升降平台分两次上升，每上升一次拟合一个圆，2个圆心形成为的直线，即为产品b的中心轴线，这样便可以中心轴线计算出其位姿角度以及位置距离。

本实施例采用2个激光轮廓传感器，成90°夹角安装，在测量时通过升降平台上升至位置1进行数据采集测量。测量系统同时获取2个激光传感器的点阵数据。激光传感器在产品b下端测得的点阵数据经数据处理成圆周坐标，即为产品b的圆周曲线坐标，通过椭圆拟合得到第1个圆心坐标(x1,y1)；激光传感器随升降平台上移一段距离f1，获取2个激光传感器数据，拟合得到第2个圆心坐标(x2,y2)，则得到三维空间的两个点(x1,y1,0),(x2,y2,f1),两点的连线即为产品b的中心轴线，依此计算出其偏转角度及位置。

实施例2：

如图3-图4所示：

偏差量测量：

在位置5，升降平台下降，用3个激光轮廓传感器测量产品b与产品a的圆周数据，形成2个点集，2个点集分别为同个圆(椭圆)圆弧中的一段；用此点集拟合圆，拟合的圆心中心与固定基座中心差值即为产品b与产品a的横向偏移量；其中，基座中心经激光器标定后作为已知量进行计算。

测量系统同时获取2个激光传感器的点阵数据。激光传感器在产品b下端测得的点阵数据经数据处理成圆周坐标，即为产品b的圆周曲线坐标，通过椭圆拟合得到第1个圆心坐标(x1,y1)；激光传感器随升降平台上移一段距离f1，获取2个激光传感器数据，拟合得到第2个圆心坐标(x2,y2)，则得到三维空间的两个点(x1,y1,0),(x2,y2,f1),两点的连线即为产品b的中心轴线，依此计算出其偏转角度及位置。

以上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，根据本发明的技术方案及其发明构思加以等同替换或改变，都应涵盖在本发明的保护范围之内。