一种基于多轴线性霍尔效应传感器的焊枪位姿识别方法

1.本发明属于自动化焊接领域，具体涉及一种基于多轴线性霍尔效应传感器的焊枪位姿识别方法


背景技术：

2.伴随着数字技术的进步，工厂自动化设备的普及化及低价化，焊接作业也从传统的手工焊接，开始向半自动焊接、自动焊接发展。同时，焊缝跟踪技术的实现，成为了自动化焊接工序合理化的必要手段。此外，高精度且高速检测及控制反馈的传感器和位移传感器的诞生，也进一步促进了焊缝跟踪技术的发展。在焊接过程中焊枪对于不同的工件和结构需面对不同的焊缝，焊接坡口或焊缝为空间位置时，为了保证焊缝成形质量效果，焊枪相对于工件待焊点的空间位置和姿态需要进行设置和控制，传统方法多是在进行焊接轨迹规划的同时实现焊枪的空间位姿设置和控制。目前，针对焊接过程中焊枪的空间位姿实时检测技术研究和应用相对较少，主要是集中在角度传感器、旋转电弧传感器和多传感器信息融合以及视觉传感等方向。
3.其中角度传感器由于其姿态的空间角度通过对陀螺仪角加速度的积分获得，其零漂移误差相对较大。而旋转电弧传感器需要对焊枪进行改造，在有限的空间内集成电机、轴承、齿轮等，机械结构复杂，加工和应用成本较高。采用多传感器信息融合技术获取焊枪相对于待焊点的空间位姿不仅系统复杂，而且要对焊枪进行改造。至于视觉传感与二维平面中的目标位置和形状识别相比，目标的空间姿态识别更加困难。
4.多轴线性霍尔效应传感器的基本原理是通过在x、y和y轴上三个独立的霍尔传感器进行磁场检测，可调节每个坐标轴的增益与偏置并计算任意两轴方向的磁场幅度和旋转角度，适用于旋转角度跟踪和检测线性位置，与其他类型的传感器相比具有高精度以及高集成度的优异性，本发明将多轴线性霍尔效应传感器、直径磁化圆筒磁铁组合，以建立数学模型的方式将其运用到焊枪空间位姿检测，弥补了霍尔效应传感器在自动焊接焊枪空间位姿检测应用领域上的空白，提供一种能有效识别焊枪位姿信息的焊枪位姿识别方法，扩展了多轴线性霍尔效应传感器的应用领域。


技术实现要素：

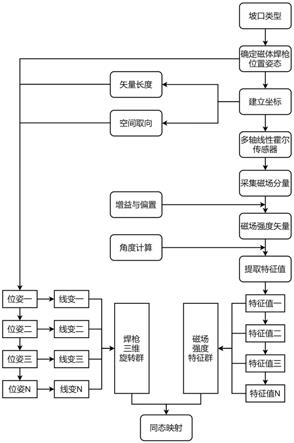
5.本发明的焊枪位姿识别方法通过以下技术方案实现：
6.一、多轴线性霍尔效应传感器与直径磁化圆筒磁铁成共轴组合放置，构建以传感器为起始点的三维向量坐标系，根据不同的焊接坡口或焊缝的空间位置及轨迹，焊枪上霍尔效应传感器与直径磁化圆筒磁铁的空间位置和姿态随时改变；
7.二、通过多轴线性霍尔效应传感器采集焊枪运动时的磁场信息，角度计算后提取磁场强度特征值，建立磁场强度特征群；
8.1、利用多轴线性霍尔效应传感器对焊枪运动时三个轴上的磁场分量信号进行伪同步采样，在采样的同时对磁场信号进行角度计算后得到磁场强度矢量在各个轴的极值和
均值坐标，既磁场强度矢量特征值，特征值集合为磁场强度特征群；
9.2、将磁场采样的时间信号分解为三个方向上的位置信号，每个方向的位置信号与其磁场强度特征值一一对应；
10.三、构建原点、矢量长度和空间取向皆可变的焊枪三维旋转群，焊枪三维旋转群与磁场强度特征群之间为同态映射关系；
11.1、在以多轴线性霍尔传感器为原点的坐标系中将焊枪位姿变化解析为原点确定、矢量长度和空间取向变化的线性变换，并以此为基底建立焊枪的三维旋转群。
12.2、磁场强度特征群与焊枪三维旋转群之间构成同态映射关系，既焊枪位姿与磁场强度特征值之间一一对应。
附图说明
13.图1是本发明实施的焊枪位姿识别方法流程框图
14.图2是多轴线性霍尔效应传感器1与直径磁化圆筒磁铁2组合位置图
15.图3为函数关系流程图
具体实施方式
16.参见图2所示多轴线性霍尔效应传感器(1)应与直径磁化圆筒磁铁(2)沿z轴放置，磁铁绕z轴(3)旋转，这样磁场在的x轴和y轴分量的响应是完全匹配的，这种布局为多轴线性霍尔效应传感器提供最简单的实现。
17.构建以传感器为起始点的三维向量坐标系，通过多轴线性霍尔效应传感器采集焊枪运动时的磁场信息，磁场快速变化时，传感器无法在同一时间t内采集不同轴的磁场分量，需要在角度计算时引入误差，为减小误差，考虑增益与偏置，需对采样样本进行平均，取时间t前后瞬间t1，t2，满足分别采集t1、t2时刻磁场在x轴上的分量x1、x2以及t时刻磁场在y轴上的分量y，使用y以及x1和x2的平均值进行角度测量。
18.进行角度测量时采用一种利用坐标数据计算角度的快速有效的方法。该算法通过执行二分法搜索，围绕原点旋转一个点，直到得到的磁场向量位于一个单轴上，从而快速逼近角度。由于坐标输入是在迭代的步骤中旋转的，所以可以通过所有步骤的总和估计出起始角。完成这些旋转后的最终位置也将产生输入矢量的大小。当与多轴霍尔效应传感器的输出一起使用时，该算法被证明是一个快速和准确的角度计算的优秀选择。因为目标是将磁场矢量与x轴对齐，所以在下一步中必须逆时针调整旋转方向。在下一次迭代中，坐标将逆时针旋转22.5
°
。这里的结果没有产生象限的变化，因此旋转的方向继续这个方向。这个过程继续进行，增加和减少角步和改变旋转方向，直到结果与x轴对齐。5次迭代后的近似角度约为19.69
°
。旋转空间坐标点的代数过程按照公式中的矩阵乘法来描述:
[0019][0020]
x
′
＝xcos(α)-ysin(α)
[0021]y′
＝xsin(α)+ycos(α)
[0022]
将cos(α)因式分解得到式：
[0023]
x
′
＝cos(α)
×
(x-ytan(α))
[0024]y′
＝cos(α)
×
(y+xtan(α))
[0025]
随着算法的发展，必须确定磁场旋转的方向。如果选择逆时针旋转，结果将产生式:
[0026]
x
′
＝cos(α)
×
(x+ytan(α))
[0027]y′
＝cos(α)
×
(y-xtan(α))
[0028]
这里唯一的区别是每个方程的运算都是反向的。因此，可以通过检查操作的符号来确定旋转的方向。这种旋转可以用一个可选择的值表示，将其表示为d
[0029][0030]
由于这种替换产生的角度大于或等于真正二分搜索中使用的期望步长，新的角步长仍然能够收敛，它可以迭代地用来确定任意磁场二维向量的角度和大小:
[0031][0032]
角度计算完成后提取磁场强度失量特征值mn(n＝1，2
……
n)组成代表磁场强度矢量特征群m
[0033]
根据传感器为起始点所建立的极坐标系，确定焊枪位姿的基失er、e
θ
和空间取向求得极坐标基矢er、e
θ
与直角坐标i，j以及空间取向的变换关系(将第一组基的两基矢分别表示为第二组基的线性组合)：
[0034][0035][0036]
写为分块矩阵形式:
[0037][0038]
以上变换可用线性代数中的过渡矩阵加以证明，证明时使用列分块来与线性代数保持一致,直角坐标中的矢量r＝xi+yj，将上述变换作逆变换得到焊枪位姿的线性代数解析公式:
[0039][0040]
不同的焊枪位姿采集对应的矢量长度e和空间取向即可得到相应的解析公式，由函数rn(n＝1,2
……
n)构成代表不同焊枪位姿的焊枪三维旋转群r。根据对磁场强度矢量特征群m的推算和定义可以推导出f:m
→
r，既r与m满足同态映射关系，任意磁场强度矢量特征值有其一一对应焊枪位姿。