一种液压振动系统的低频拓展控制方法与流程

本发明属于力学环境振动试验领域，尤其涉及一种液压振动系统的低频扩展控制方法。

背景技术：

振动试验装备主要包括振动台和振动控制系统两个方面。振动台是振动环境模拟的物理基础和实现载体。控制系统是对振动台的运动进行控制的运算程序。力学环境试验中包含各种类型的环境模拟，如低频振动、高频振动、大推力大位移振动等。其中低频振动和大位移振动试验通常需要采用液压振动试验装备。由于液压振动台具有输出位移大，功率大和低频性能好等优点，在汽车、重载设备和大型结构的振动试验中具有不可替代的地位，由于液压振动试验系统的固有频率低，振动试验的起点频率可以达到0.5HZ以下，因此液压振动系统常用在道路谱的模拟，地震波谱的模拟等低频振动的领域中，同时由于液压振动系统的执行机构采用的是伺服油缸，其振动最大位移可达30cm以上，这也是其他类型的振动试验装备所无法达到的，然而液压振动系统由于阻尼比小，稳定裕量低，在超出其固有频率时性能较差，导致振动试验频带太窄。

液压振动台是在电液伺服技术的推动下发展起来的，伺服控制技术可以实现液压振动台的基本运动控制，并且保证液压振动台具有足够的稳定性和频宽。使用液压振动台可以模拟正弦、随机、正弦加随机等多种振动环境，但是液压振动台的频宽低，当负载特性发生变化或者振动环境模拟所要求的精度和频宽超出其工作能力时会导致振动台面不按照期望的运动规律进行运动，因此就需要相应的控制技术对振动台的低频性能进行补偿控制。

技术实现要素：

为了解决现有技术中液压振动台的低频性能差、试验频带窄的问题，本发明提出了一种液压振动系统的低频拓展控制方法，所述方法包括：步骤1：根据液压振动系统的技术参数分别对伺服阀、伺服油缸、振动台建立负载特性方程；步骤2：将建立的负载特性方程进行拉普拉斯变换得到频域内液压振动系统的开环传递函数；步骤3：根据液压振动系统的开环传递函数画出初始频响特性曲线，确定液压振动系统的初始固有频率，分析所述液压振动系统的初始低频特性；步骤4：画出液压振动系统在输出反馈下的根轨迹，在根轨迹图上确定液压振动系统的稳定范围、阻尼比变化情况和临界稳定时的反馈增益值；步骤5：分析输出反馈和状态反馈的情况下液压振动系统的固有频率变化；步骤6：根据状态反馈后的固有频率的变化情况确定状态反馈变量，并计算当状态反馈后的固有频率最大时状态反馈增益系数值；步骤7：根据液压振动系统在输出反馈和状态反馈下的等效传递函数，确定前馈控制的阶数和控制系数；步骤8：对所述液压振动系统进行频响函数的校正计算，根据校正计算结果对输入信号进行修正。

优选地，所述技术参数包括以下一项或多项：供油压力、伺服阀流量、伺服阀阻尼比、伺服阀频宽、液压动力机构阻尼比、油液体积弹性模量、活塞作用面积、伺服油缸行程、液压系统开环增益。

优选地，所述伺服阀的负载特性方程为：

Q_fuzai＝Ｑ₀-K_PP_fuzai

其中Ｑ_fuzai为负载流量；K_P为单位负载压力变化所产生的负载流量增益；P_fuzai为伺服油缸负载压强，Q₀为伺服阀空载流量；

所述伺服油缸的负载特性方程为：

$Q_{fuzai}=A\frac{dY}{dt}+C_{xielou}{P}_{fuzai}+\frac{V}{4\mathrm{\β}}\frac{{\mathrm{dP}}_{fuzai}}{dt}$

其中Ｑ_fuzai为负载流量，β为油液的弹性模量，A为活塞作用面积；Y为输出位移；C_xielou为伺服油缸泄漏系数；P_fuzai为伺服油缸负载压强；V为伺服油缸体积；t为时间；

所述振动台的负载特性方程为：

${\mathrm{AP}}_{fuzai}=M\frac{d^{2}Y}{{\mathrm{dt}}^2}$

A为活塞作用面积；Y为输出位移；P_fuzai为负载压强；M为振动台面及负载的质量。

优选地，所述液压振动系统的开环传递函数：

$G\left(s\right)=\frac{Y\left(s\right)}{U\left(s\right)}=\frac{K_m}{(\frac{s^2}{{{\mathrm{\ω}}_1}^2}+\frac{2{\mathrm{\ξ}}_1}{{\mathrm{\ω}}_1}s+1)s(\frac{s^2}{{{\mathrm{\ω}}_2}^2}+\frac{2{\mathrm{\ξ}}_2}{{\mathrm{\ω}}_2}s+1)}$

其中：

${\mathrm{\ω}}_2=\sqrt{\frac{4{\mathrm{\βA}}^2}{MV}};{\mathrm{\ξ}}_2=\frac{{\mathrm{\ω}}_{2}M(K_P+C_{xielou})}{2A^2}$

G(s)为输入电压到输出位移的开环传递函数；Y(s)为输出位移的拉氏变换；U(s)为输入电压的拉氏变换；ω₁、ω₂分别为伺服阀和液压作动机构的固有频率，ξ₁为伺服阀的阻尼比；ξ₂为液压作动机构的阻尼比，K_m为开环系统的整体增益。

优选地，所述步骤3进一步包括：

根据步骤2的开环传递函数画出初始频响特性曲线，在初始频响特性曲线上确定峰值点或转折点所对应的频率值，以此确定所述液压振动系统的初始固有频率，并分析所述液压振动系统的初始低频特性。

优选地，根据步骤2的开环传递函数画出初始频响特性曲线具体为：

将所述液压振动系统的传递函数分解为一阶环节和二阶环节，分别画出一阶环节和二阶环节的频响特性曲线，将一阶环节和二阶环节的频响曲线叠加得到液压振动系统的初始频响特性曲线。

优选地，所述输出反馈下的液压振动系统中的开环传递函数为：

$G_k\left(s\right)=K_{df}\frac{K_m}{(\frac{s^2}{{{\mathrm{\ω}}_1}^2}+\frac{2{\mathrm{\ξ}}_1}{{\mathrm{\ω}}_1}s+1)s(\frac{s^2}{{{\mathrm{\ω}}_2}^2}+\frac{2{\mathrm{\ξ}}_2}{{\mathrm{\ω}}_2}s+1)}=K_{df}G\left(s\right)$

所述闭环特征方程的一般表达式为：

$\frac{K_{df}f}{\underset{l=1}{\overset{n}{\Π}}(s+p_l)}=-1$

K_m为开环系统的整体增益，K_df为输出反馈增益值，f表示等效变换后的常数，p_l表示系统的极点。

优选地，根据所述闭环特征方程的一般表达式确定出特征方程的根随参数K_df的变化情况，并画出液压振动系统的闭环根轨迹；在闭环根轨迹图上确定液压振动系统输出反馈的稳定范围、液压振动系统在输出反馈时阻尼比变化情况和和临界稳定时的反馈增益值，并分析液压振动系统的阻尼比变化情况对液压系统的振荡特性和过渡时间的影响。

优选地，首先，根据液压振动系统输出反馈下的等效传递函数，画出输出反馈后的频响特性曲线，在输出反馈后的频响特性曲线上确定峰值点或转折点所对应的频率值，以此确定系统输出反馈后的固有频率，观察输出反馈后的固有频率的变化情况；

其次，分析各个状态反馈变量反馈控制对液压振动系统固有频率的影响，即根据液压振动系统在各个状态反馈下的等效传递函数画出状态反馈后的频响特性曲线，在状态反馈后的频响特性曲线上确定峰值点或转折点所对应的频率值，以此确定液压振动系统状态反馈后的固有频率，观察状态反馈后的固有频率的变化情况。

优选地，所述液压振动系统在输出反馈和状态反馈的情况下的等效传递函数为：

$G_d\left(s\right)=\frac{K_m}{(\frac{s^2}{{{\mathrm{\ω}}_1}^2}+\frac{2{\mathrm{\ξ}}_1}{{\mathrm{\ω}}_1}s+1)(\frac{s^2}{{{\mathrm{\ω}}_2}^2}+\frac{2{\mathrm{\ξ}}_2}{{\mathrm{\ω}}_2}s+1)s+K_m(K_{df}+as+{\mathrm{bs}}^2+{\mathrm{cs}}^3)}.$

本发明的一种用于拓展液压振动台试验频宽的控制方法，实现了液压振动台在低频性能的提升和频宽的拓展。本方法在传统输出反馈的基础上提出了输出反馈和状态反馈相结合的方法。针对液压振动台固有频率太低，使用频宽太窄的现状，针对整个液压振动系统的频响特性在频域内对其进行补偿修正。整个低频拓展的控制方法包括：两个闭环控制，其中内环控制采用输出反馈、状态反馈和前馈相结合的控制方式在一定程度上提高液压振动台的固有频率，外环控制在频域内实时辨识系统的频响函数，根据辨识的系统频响函数对系统输入进行补偿修正从而进一步拓展液压系统的振动试验频宽。与现有技术相比，本发明的优点如下；

针对整个液压振动系统采用输出反馈、前馈和状态反馈相结合的控制方式对液压系统低频性能进行提升，并且采用系统辨识的方式在一定频域范围内对液压系统的输入信号进行补偿，本发明能够将液压系统的频宽拓展的更宽，低频性能更好。振动试验的精度更高。

附图说明

图1是本发明的一种液压振动系统低频拓展控制方法的流程图；

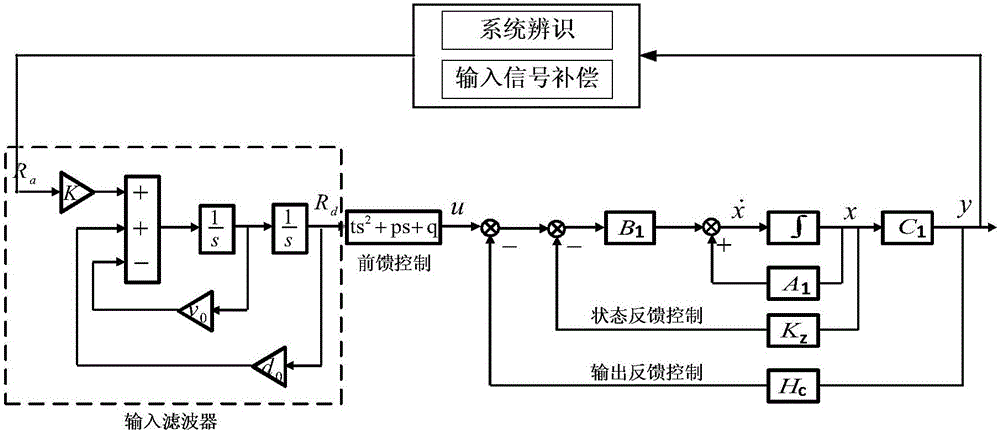
图2是本发明的一种液压振动系统低频拓展控制方法的控制框图；

图3所示为对所述液压振动系统进行频响函数的校正计算和输入信号的修正流程图；

图4是本发明的一个实施实例中的根轨迹图；

图5是本发明的一个实施实例中控制前后的系统频响函数的对比图。

具体实施方式

下面结合附图1-5及具体实施例对本发明作进一步详细说明。

图1所示为本发明的一种液压振动系统低频拓展控制方法的流程图。

步骤1：根据液压振动系统的技术参数分别对伺服阀、伺服油缸、振动台建立负载特性方程。

所述技术参数包括以下一项或多项：供油压力、伺服阀流量、伺服阀阻尼比、伺服阀频宽、液压动力机构阻尼比、油液体积弹性模量、活塞作用面积、伺服油缸行程、液压系统开环增益等。

所述液压振动系统采用液压参数对称的单活塞杆伺服油缸，伺服阀采用对称式电液伺服阀。所述液压振动系统的重力由初始供油压力与之平衡，重力不计算在负载方程中，运动过程中不计油路压力损失以利于模型的简化与分析。

所述伺服阀的空载特性与其固有频率和阻尼比有关，用二阶环节进行表示：

Q₀为伺服阀空载流量；I输入电流；K_I流量电流增益；ω₁伺服阀固有频率；ξ₁伺服阀阻尼比；s表示一个复数，s可以与频率关联起来，这时s等效被看成jω。因此将s＝jω代入后，就可以用来分析信号频谱上的特性。由于拉氏变换性质，s的实部、虚部、模长、相角等可以与系统性能相关联起来。

所述伺服阀的负载特性方程为：

Ｑ_fuzai＝Ｑ₀-K_PP_fuzai方程(2)

其中Q_fuzai为负载流量；K_P为单位负载压力变化所产生的负载流量增益；P_fuzai为伺服油缸负载压强。

所述伺服油缸中流量变化方程，主要包括三部分：一是推动活塞做功，二是泄露，三是油液的可压缩性；所述伺服油缸的负载特性方程为：

β为油液的弹性模量，Ｑ_fuzai为负载流量；A为活塞作用面积；Y为输出位移；C_xielou为伺服油缸泄漏系数；P_fuzai为伺服油缸负载压强；V为伺服油缸体积；t为时间。

所述振动台的负载特性方程，由牛顿第二定律建立：

A为活塞作用面积；Y为输出位移；P_fuzai为伺服油缸负载压强；M为振动台面及负载的质量。

步骤2：将建立的负载特性方程进行拉普拉斯变换得到频域内液压振动系统的开环传递函数。

具体地，将步骤1所述的方程(1)、(2)、(3)、(4)联立(将方程1代入方程2消去Ｑ₀后联立方程3和方程4消去Ｑ_fuzai和P_fuzai)并进行拉普拉斯变换得到液压振动系统的开环传递函数：

其中：

G(s)为输入电压到输出位移的开环传递函数；Y(s)为输出位移的拉氏变换；U(s)为输入电压的拉氏变换；ω₁、ω₂分别为伺服阀和液压作动机构的固有频率，ξ₁为伺服阀的阻尼比；ξ₂为液压作动机构的阻尼比，K_m为开环系统的整体增益。

步骤3：根据液压振动系统的开环传递函数画出初始频响特性曲线，确定液压振动系统的初始固有频率，分析所述液压振动系统的初始低频特性。

液压振动系统的频响特性曲线是一个一阶环节和两个二阶环节响应的叠加。将液压振动系统的传递函数分解为一阶环节和二阶环节，分别画出一阶环节和二阶环节的幅频曲线之后叠加即得到液压振动系统的频响特性曲线。

具体地，根据步骤2的开环传递函数画出初始频响特性曲线，在初始频响特性曲线上确定峰值点或转折点所对应的频率值，以此确定所述液压振动系统的初始固有频率，并分析所述液压振动系统的初始低频特性。

进一步地，根据步骤2的开环传递函数画出初始频响特性曲线具体为：将所述液压振动系统的传递函数分解为一阶环节和二阶环节，分别画出一阶环节和二阶环节的频响特性曲线，将一阶环节和二阶环节的频响曲线叠加得到液压振动系统的初始频响特性曲线。

步骤4：画出液压振动系统在输出反馈下的根轨迹，在根轨迹图上确定液压振动系统的稳定范围、阻尼比变化情况和临界稳定时的反馈增益值。

输出反馈下的液压振动系统中的开环传递函数(在控制理论中的概念是指：在由输出反馈构成的系统是一个闭环系统，它的开环传递函数是指由输入到反馈的传递函数)可以表示为：

其中K_m为开环系统的整体增益，K_df即为输出反馈的增益值。

闭环特征方程为：

1+K_dfG(s)＝0方程(8)

即

K_df为输出反馈增益值，f表示等效变换后的常数，p_l表示系统的极点。

方程(9)为闭环特征方程的一般表达式，表示液压振动系统的闭环极点与其开环零极点之间的关系，根据方程(9)可以确定出特征方程的根随参数K_df的变化情况，并画出液压振动系统的闭环根轨迹；在闭环根轨迹图上确定液压振动系统输出反馈的稳定范围、液压振动系统在输出反馈时阻尼比变化情况和和临界稳定时的反馈增益值(临界稳定是一个临界的状态，只对应一个反馈增益值)，并分析液压振动系统的阻尼比变化情况对液压系统的振荡特性和过渡时间的影响。

所述根轨迹如图4所示，在虚轴左边的区域即为稳定区域，离虚轴近的极点为液压振动系统的主导极点，液压振动系统的主要特性也由其决定，在主导极点运动的过程中，可以在图4上确定液压振动系统的阻尼比变化情况。

步骤5：分析输出反馈和状态反馈的情况下液压振动系统的固有频率变化。

首先，根据液压振动系统输出反馈下的等效传递函数，画出输出反馈后的频响特性曲线，在输出反馈后的频响特性曲线上确定峰值点或转折点所对应的频率值，以此确定系统输出反馈后的固有频率，观察输出反馈后的固有频率的变化情况。

所述液压振动系统输出反馈下的等效传递函数为：

其中，G(s)为输入电压到输出位移的开环传递函数，K_df为输出反馈增益值。

其次，分析各个状态反馈变量反馈控制对液压振动系统固有频率的影响，即根据液压振动系统在各个状态反馈下的等效传递函数画出状态反馈后的频响特性曲线，在状态反馈后的频响特性曲线上确定峰值点或转折点所对应的频率值，以此确定液压振动系统状态反馈后的固有频率，观察状态反馈后的固有频率的变化情况。

所述状态反馈的等效传递函数(用G_zhuangtai(Ｓ)表示)为：

其中a、b、c分别对应状态反馈变量x₁、x₂、x_３的反馈增益系数。

图2为本发明的一种液压振动系统的控制图。输入滤波器是将加速度信号R_a转换成位移信号R_d；K、v₀、d₀均为输入滤波器的系数；矩阵A₁、B₁、C₁由液压振动系统本身所决定；输出反馈H_c为位移反馈；状态反馈K_z为速度x₁、加速度x₂、负载压强的变化率x₃所构成的综合反馈。其中状态反馈变量x₁(速度)和x₂(加速度)可由传感器测量得到。由方程(4)可得：

AP_fuzai＝Mx₂方程(12)

其中，A为活塞作用面积、P_fuzai为伺服油缸负载压强。

因此，状态反馈变量x₃可以通过求解负载压强的变化值来得出，而负载压力的变化值又可以通过伺服阀负载特性方程进行求解，具体解法如下：

而

K_P为负载压力变化所产生的负载流量增益，表示伺服阀阀芯的移动速度，K_v为阀芯位移所产生的负载流量增益。

液压振动系统的控制框图如图2所示，在输出反馈的前提下引入状态反馈控制。

步骤6：根据步骤5中状态反馈后的固有频率的变化情况确定状态反馈变量，并计算当状态反馈后的固有频率最大时状态反馈增益系数值。

具体地，根据步骤5中状态反馈后的固有频率的变化情况确定状态反馈变量，并计算当状态反馈后的固有频率最大时状态反馈增益系数a、b、c的值，其中a、b、c分别对应状态反馈变量x₁、x₂、x₃的反馈增益系数。

步骤7：根据液压振动系统在输出反馈和状态反馈下的等效传递函数，确定前馈控制的阶数和控制系数。

通过前馈控制即零极点对消的方式来提高液压振动系统的固有频率。

根据图2，液压振动系统在输出反馈和状态反馈的情况下的等效传递函数为：

根据高阶系统的频响特性的叠加原理将液压振动系统在输出反馈和状态反馈的情况下的等效传递函数分解为等效的一阶环节和二阶环节的组合函数：

K_o为等效变换后的常数、ω_m、ω_n为等效传递函数中二阶环节的频率，ξ_m、ξ_n为等效传递函数中二阶环节的阻尼比、ω_q等效传递函数中一阶环节的频率。

根据组合函数分析此时影响系统低频特性的是哪一等效环节，然后引入前馈控制后，确定此时的等效传递函数如方程(17)所示，(将输入变量进入液压系统前，对其进行比例与积分运算)让系统的零点和极点相等。

其中，t、p、q为前馈控制的控制系数。

液压振动系统在输出反馈和状态反馈下的等效传递函数即为方程(15)，将反馈增益系数代入即可。

确定前馈控制的阶数具体为：前馈控制的阶数根据方程(16)确定，即比较ω_mω_n、ω_q的大小，如果ω_q最小，则为一阶，否则为二阶。

控制系数就是方程(17)中的t、p、q，通过方程(17)中零点与频率最小的极点相等即可求解确定。

所述步骤4-7为内环控制。

步骤8：对所述液压振动系统进行频响函数的校正计算，根据校正计算结果对输入信号进行修正。校正后的系统频响函数记为：H(f)。

图3所示为对所述液压振动系统进行频响函数的校正计算和输入信号的修正流程图。

首先，采用H₁和H₂的计算方法计算液压振动系统的频响函数，其中H₁是将输入信号与输出信号的互功率谱除以输入信号的自功率谱，H₂是将输出信号的自功率谱除以输入信号与输出信号的互功率谱。(S_xy：输入信号与输出信号的互功率谱；S_xx：输入信号的自功率谱；S_yy：输出信号的自功率谱。)

其次，根据输入和输出的噪声影响系数，对液压振动系统的频响函数校正计算，从而提高计算精度。所述噪声影响系数包括输入、输出噪声所占的比重。

其中校正公式为：

H(f)＝δH₁+ηH₂ 方程(18)

H(f)表示校正系统频响函数的值，δ表示输入噪声所占的比重，η表示输出噪声所占的比重。

根据校正公式计算的频响函数的校正计算结果对输入信号进行修正。

所述步骤8为外环控制。

本方法是拓展液压振动系统的频宽，步骤4-7属于内环控制，从系统的属性上提高固有频率，也是为步骤8做一个铺垫。步骤8为外环控制，是在内环控制的基础上进一步拓展液压振动系统的使用频宽。

本发明的效果图如图5，可以看出采用该方法后液压振动系统的频宽得到了较大的拓展，低频性能得到了提升。

尽管上文对本发明的具体实施方式给予了详细描述和说明，但是应该指明的是，我们可以依据本发明的构想对上述方式进行各种等效改变和修改，其所产生的功能作用仍未超出说明书及附图所涵盖的精神时，均应在本发明的保护范围之内。