一种基于压缩存储和列选主元高斯消去法的airPLS实现方法与流程

本发明涉及一种数据的预处理方法，尤其涉及一种基于压缩存储和列选主元高斯消去法的airPLS实现方法。

背景技术：
拉曼光谱分析技术是基于拉曼散射效应，对与入射光频率不同的散射光谱进行分析以得到分子振动、转动方面信息，并应用于分子结构研究的一种分析方法，因其能够提供快速、简单、可重复且无损伤的定性定量分析，被广泛应用于各种化学物质的检验，如环境科学、司法鉴定、安全检查、珠宝鉴定、晶体研究以及药品鉴定等诸多领域。拉曼光谱分析中，最主要的干扰因素是荧光。由于有机分子或样品中污染物的荧光影响，常会使拉曼光谱产生荧光背景信号，表现为一个典型的倾斜宽背景，使基线偏离，信噪比下降，影响数据的进一步分析处理，因此在分析前必须预先扣除荧光背景。目前常用的背景扣除方法主要有：频域滤波、小波变换、多项式拟合以及各种基于最小二乘的算法等。其中自适应迭代惩罚最小二乘法(airPLS,adaptiveiterativelyreweightedPenalizedLeastSquares)是一种新的光谱背景扣除方法，相比于其它方法，airPLS无需掌握任何先验信息，无需人为干预，即可全自动地对光谱进行处理。但是这种背景扣除算法目前只能在计算机系统上运行，无法直接在嵌入式系统中使用。

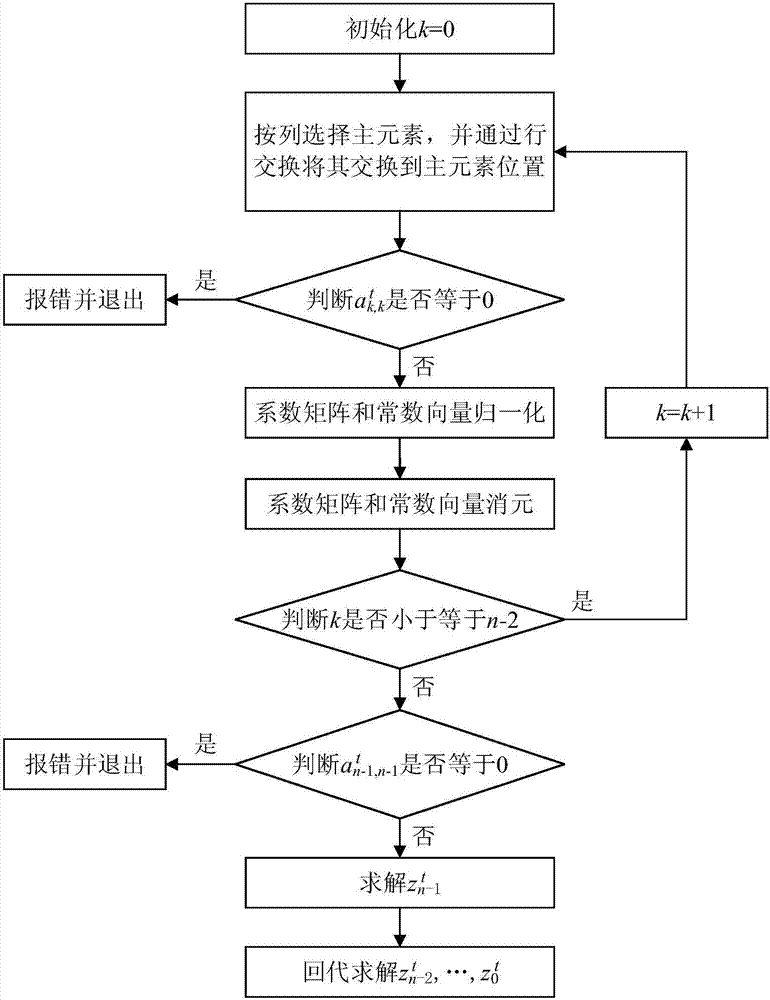
技术实现要素：
为了克服现有airPLS背景扣除算法存在的局限性，本发明根据嵌入式系统的特点，提出了一种基于压缩存储和列选主元高斯消去法的airPLS实现方法，该方法利用压缩存储的方式只存储高阶带型矩阵带区内的非零元素；利用列选主元高斯消去法求解原始数据与拟合数据之间的线性方程组；从而对存储空间和计算量要求较低，可在嵌入式平台上实现快速荧光背景扣除。本发明解决其技术问题所采用的方案：一种基于压缩存储和列选主元高斯消去法的airPLS实现方法，具体包括如下步骤：(1)初始化：初始化n×n权重对角矩阵W0，使其对角线元素为其余元素全为0，W0的右上标0表示迭代次数t＝0的时刻，n表示光谱数据长度；已知(n-2)×n二阶微分矩阵D为则其中，λ是一个用户可调的平滑参数。由上式可知，λDTD是一个n×n阶带型矩阵。采用压缩存储的方法，用一个n行、5列的二维数组B(0:n-1,0:4)来存放λDTD中带区内的元素，具体如下：将带型矩阵λDTD中的行与二维数组B中的行一一对应；将带型矩阵λDTD中每一行上带区内的元素以左边对齐顺序存放在二维数组B中的相应行中，而对于前2行与最后2行中最右边的空余部分均填入0。则与带型矩阵λDTD所对应的二维数组B如下：根据用户预设的迭代次数m，对于t从0到m做如下步骤(2)-步骤(3)的迭代运算：(2)记At＝Wt+λDTD、Yt＝Wtx，其中，Wt表示迭代时刻t的权重对角矩阵，x为1×n原始拉曼光谱数据向量；At和Yt满足关系Atzt＝Yt，其中zt为1×n迭代时刻t的拟合输出数据向量，得zt＝(Wt+λDTD)-1Wtx＝(At)-1Yt；(3)采用列选主元高斯消去法，求解线性方程组zt＝(At)-1Yt，具体步骤如下：(3.1)对于k从0到n-2做以下运算：(3.1.1)按列选择主元素表示矩阵At的第i行、第j列元素，通过行交换将绝对值最大的元素交换到主元素位置上；(3.1.2)判断是否等于0，若是，则退出；若否，则继续下一步；(3.1.3)系数矩阵归一化(3.1.4)常数向量归一化(3.1.5)系数矩阵消元(3.1.6)常数向量消元通过步骤(3.1.1)-步骤(3.1.6)后，Atzt＝Yt变成：(3.2)回代求解：判断是否等于0；若是，则退出；若否，则继续下一步解出回代逐个解出判断t是否达到预设迭代次数m或满足收敛条件：若否，则t＝t+1，并根据下式重新计算权重系数更新Wt，返回步骤(2)；其中，表示迭代时刻t时，Wt中第i行、第i列元素；xi表示原始光谱数据向量x中第i个元素，表示迭代时刻t-1时得到的拟合数据向量zt-1的第i个元素，|dt|表示原始光谱数据向量x与t-1时刻得到的拟合数据向量zt-1的差值为负的所有元素的绝对值之和；若是，则结束，输出拟合数据向量zt，zt即为所求的原始光谱数据x扣除荧光背景后的结果。进一步的，所述步骤(3.2)中收敛条件为：|dt|<0.001×|x|，其中，|x|表示原始光谱数据向量x的所有元素的绝对值之和。本发明的有益效果是：(1)采用了压缩存储的方法，与矩阵元素全部存储的方式相比，使得对矩阵变量存储空间从n×n变为5×n，相当于压缩了n/5倍，对处理器的存储空间要求大大降低，数据长度越长，即n越大，这种存储方式的优势越明显；而且由于压缩后的行号与原矩阵中的行号相同，给运算带来很大的方便。(2)采用列选主元高斯消去法来求解拟合数据向量，解决了常规的高斯消去法存在数值稳定性问题和全选主元高斯消去法在选主元素时需要花费较多机器时间的问题，在算法性能和计算复杂度方面做了较好的权衡。(3)本发明提出的方法可以在包括嵌入式系统在内的各类硬件平台上使用，对处理器的存储空间和计算能力要求较低，可以从复杂光谱中提取有用的光谱信息，提高了光谱辨识、定性和定量分析的准确度，便于在此基础上开发低成本的便携式拉曼光谱仪。本发明在嵌入式平台上的实测结果与仿真结果完全一致。附图说明下面结合附图和实施例对本发明进一步说明；图1是本发明的流程图；图2是本发明中列选主元高斯消去法流程图；图3是本发明实施例中酒精原始拉曼光谱图；图4是采用本发明扣除背景后的酒精拉曼光谱图。具体实施方式下面结合附图和实施例对本发明作进一步说明。如图1所示，本发明实施例提供一种基于压缩存储和列选主元高斯消去法的airPLS实现方法，具体包括如下步骤：(1)初始化：初始化n×n权重对角矩阵W0，使其对角线元素为其余元素全为0，W0的右上标0表示迭代次数t＝0的时刻，n表示光谱数据长度；已知(n-2)×n二阶微分矩阵D为则其中，λ是一个用户可调的平滑参数。由上式可知，λDTD是一个n×n阶带型矩阵，除了5条对角线上的元素为非零以外，其它的所有元素均为零。通常情况下，n远远大于5，可得带型矩阵中绝大部分为零元素。为了节省存储空间，采用压缩存储的方法，即只存储5条对角线上的元素，用一个n行、5列的二维数组B(0:n-1,0:4)来存放λDTD中带区内的元素，具体如下：将带型矩阵λDTD中的行与二维数组B中的行一一对应；将带型矩阵λDTD中每一行上带区内的元素以左边对齐顺序存放在二维数组B中的相应行中，而对于前2行与最后2行中最右边的空余部分均填入0。则与带型矩阵λDTD所对应的二维数组B如下：在这种压缩存储方式中，虽然前2行与最后2行还保留有部分零元素，但与矩阵元素全部存储的方式相比，存储空间减少了n/5倍，数据长度越长，即n越大，这种存储方式的优势越明显；而且由于压缩后的行号与原矩阵中的行号相同，给运算带来很大的方便。根据用户预设的迭代次数m，对于t从0到m做如下步骤(2)-步骤(3)的迭代运算：(2)记At＝Wt+λDTD、Yt＝Wtx，其中，Wt表示迭代时刻t的权重对角矩阵，x为1×n原始拉曼光谱数据向量；At和Yt满足关系Atzt＝Yt，其中zt为1×n迭代时刻t的拟合输出数据向量，得zt＝(Wt+λDTD)-1Wtx＝(At)-1Yt；(3)为了求解该线性方程组zt＝(At)-1Yt，可以采用高斯消去法。常规的高斯消去法存在数值稳定性问题，而全选主元高斯消去法在选主元素时需要花费较多的机器时间。因此，本发明采用列选主元高斯消去法，如图2所示，具体步骤如下：(3.1)对于k从0到n-2做以下运算：(3.1.1)按列选择主元素表示矩阵At的第i行、第j列元素，通过行交换将绝对值最大的元素交换到主元素位置上；(3.1.2)判断是否等于0，若是，则退出；若否，则继续下一步；(3.1.3)系数矩阵归一化(3.1.4)常数向量归一化(3.1.5)系数矩阵消元(3.1.6)常数向量消元通过步骤(3.1.1)-步骤(3.1.6)后，Atzt＝Yt变成：在上述操作过程中，每次在系数矩阵中依次按列在主对角线及以下的元素中，选取绝对值最大的元素作为主元，将它调到主对角线上，然后用它消去主对角线以下的元素，最后化为同解的上三角形方程组去求解。(3.2)回代求解：判断是否等于0；若是，则退出；若否，则继续下一步解出回代逐个解出由上可知，本发明采用的列选主元高斯消去法计算简单，且具有良好的数值稳定性。判断t是否达到预设迭代次数m或满足收敛条件：若否，则t＝t+1，并根据下式重新计算权重系数更新Wt，返回步骤(2)；其中，表示迭代时刻t时，Wt中第i行、第i列元素；xi表示原始光谱数据向量x中第i个元素，表示迭代时刻t-1时得到的拟合数据向量zt-1的第i个元素，|dt|表示原始光谱数据向量x与t-1时刻得到的拟合数据向量zt-1的差值为负的所有元素的绝对值之和；若是，则结束，输出拟合数据向量zt，zt即为所求的原始光谱数据x扣除荧光背景后的结果。所述步骤(3.2)中，迭代次数m可由用户根据计算量和性能自己设定，收敛条件可为：|dt|<0.001×|x|，其中，|x|表示原始光谱数据向量x的所有元素的绝对值之和。通过上述步骤，在保证airPLS算法性能的前提下，大大降低其对处理器的存储空间和计算能力的要求，使得airPLS算法能够在包括嵌入式系统在内的各类硬件平台上使用，便于在此基础上开发低成本的便携式拉曼光谱仪。实施例：以光谱仪采集的酒精样品数据为例(数据长度n＝3000)，其原始拉曼光谱如图3所示。由图3可知，其拉曼光谱由于受到荧光背景的干扰，导致基线产生偏离，降低了光谱的信噪比，容易引起谱线的误识和漏识。利用本发明提出的背景扣除方法对该数据进行处理，预设迭代次数m＝5，平滑参数λ＝105。将带型矩阵λDTD每个元素存为32位的浮点型，若采用矩阵元素全部存储的方式，则所需的存储空间为3000×3000×4Byte＝34.3MByte，远远超过一般嵌入式处理器的RAM容量；若采用本发明提出的压缩存储方式，则所需存储空间可缩减为5×3000×4Byte＝58.6kByte，STM32F107VC等常见嵌入式处理器即可满足该需求。同时，若用全选主元高斯消去法对方程组进行求解，选主元操作的时间复杂度为O(n2)，对于高阶矩阵时间消耗量非常大，对处理器的计算能力要求较高；若采用本发明的列选主元高斯消去法，考虑到矩阵中的非零元素是带状的，带宽为5，带区外元素均为零，因此选主元操作只须按列在半带宽范围进行，其时间复杂度为O(2)。此外，其归一化和消元过程也只涉及带区内的元素，计算量大大降低。为了便于能够移植到各类嵌入式平台上，利用C语言对本发明方法进行了实现。经过本实现方法处理后的光谱如图4所示。由图4可知，本方法有效地去除了荧光背景的影响，将有用的拉曼光谱信息准确地显现出来，提高了光谱辨识、定性和定量分析的准确度，在嵌入式平台上的实测结果与仿真结果完全一致。