一种基于压缩存储和列选主元高斯消去法的airPLS实现方法与流程

技术特征：
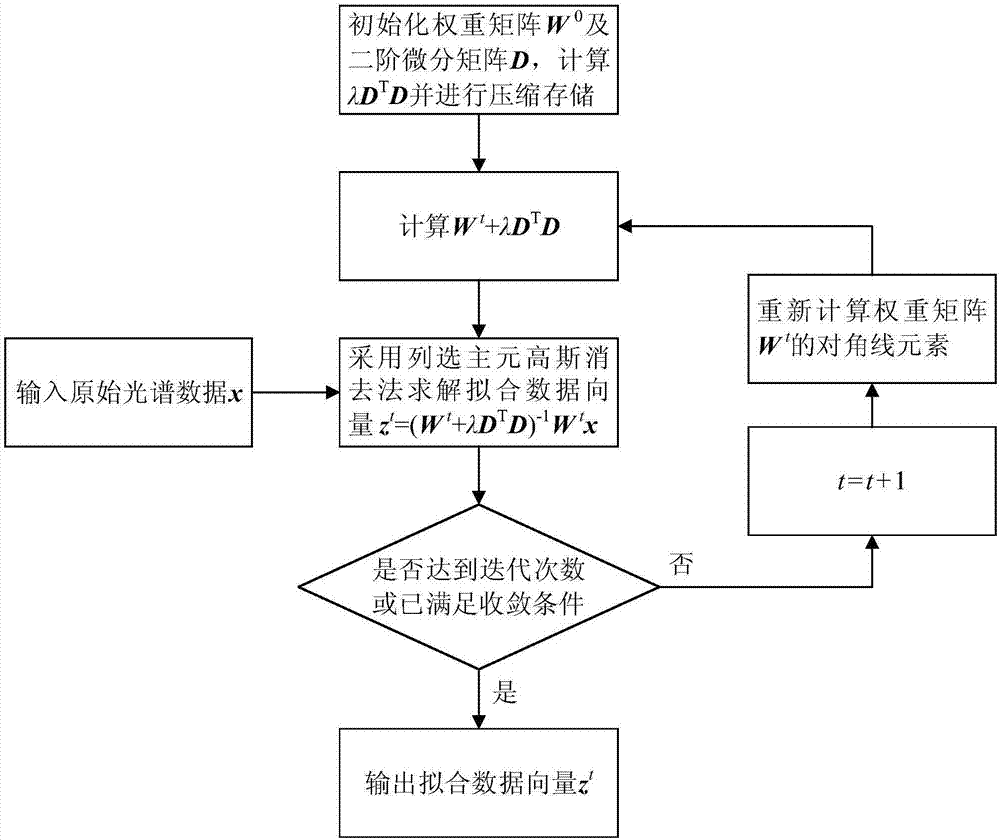
1.一种基于压缩存储和列选主元高斯消去法的airPLS实现方法，其特征在于，具体包括如下步骤：(1)初始化：初始化n×n权重对角矩阵W0，使其对角线元素为其余元素全为0，W0的右上标0表示迭代次数t＝0的时刻，n表示光谱数据长度；已知(n-2)×n二阶微分矩阵D为则其中，λ是一个用户可调的平滑参数；由上式可知，λDTD是一个n×n阶带型矩阵；采用压缩存储的方法，用一个n行、5列的二维数组B(0:n-1,0:4)来存放λDTD中带区内的元素，具体如下：将带型矩阵λDTD中的行与二维数组B中的行一一对应；将带型矩阵λDTD中每一行上带区内的元素以左边对齐顺序存放在二维数组B中的相应行中，而对于前2行与最后2行中最右边的空余部分均填入0；则与带型矩阵λDTD所对应的二维数组B如下：根据用户预设的迭代次数m，对于t从0到m做如下步骤(2)-步骤(3)的迭代运算：(2)记At＝Wt+λDTD、Yt＝Wtx，其中，Wt表示迭代时刻t的权重对角矩阵，x为1×n原始拉曼光谱数据向量；At和Yt满足关系Atzt＝Yt，其中zt为1×n迭代时刻t的拟合输出数据向量，得zt＝(Wt+λDTD)-1Wtx＝(At)-1Yt；(3)采用列选主元高斯消去法，求解线性方程组zt＝(At)-1Yt，具体步骤如下：(3.1)对于k从0到n-2做以下运算：(3.1.1)按列选择主元素K＝min(k+2,n-1),表示矩阵At的第i行、第j列元素，通过行交换将绝对值最大的元素交换到主元素位置上；(3.1.2)判断是否等于0，若是，则退出；若否，则继续下一步；(3.1.3)系数矩阵归一化(3.1.4)常数向量归一化(3.1.5)系数矩阵消元(3.1.6)常数向量消元通过步骤(3.1.1)-步骤(3.1.6)后，Atzt＝Yt变成：(3.2)回代求解：判断是否等于0；若是，则退出；若否，则继续下一步解出回代逐个解出判断t是否达到预设迭代次数m或满足收敛条件：若否，则t＝t+1，并根据下式重新计算权重系数更新Wt，返回步骤(2)；其中，表示迭代时刻t时，Wt中第i行、第i列元素；xi表示原始光谱数据向量x中第i个元素，表示迭代时刻t-1时得到的拟合数据向量zt-1的第i个元素，|dt|表示原始光谱数据向量x与t-1时刻得到的拟合数据向量zt-1的差值为负的所有元素的绝对值之和；若是，则结束，输出拟合数据向量zt，zt即为所求的原始光谱数据x扣除荧光背景后的结果。2.根据权利要求1所述的基于压缩存储和列选主元高斯消去法的airPLS实现方法，其特征在于，所述步骤(3.2)中收敛条件为：|dt|<0.001×|x|，其中，|x|表示原始光谱数据向量x的所有元素的绝对值之和。