一种动力电池开路电压的估计方法与流程

本申请涉及电动汽车技术领域，具体涉及一种动力电池开路电压的估计方法。

背景技术：

电池荷电状态(stateofcharge,soc)估计是电池管理系统中最基础也是最重要的部分，准确的soc估计不仅可以准确的监控电池的状态、优化功率分配、在一定程度上延长单次充满电的续航里程，还可以防止电池出现过充、过放、起火甚至爆炸等情况。然而，动力电池的soc不能通过仪器直接测量，只能通过电流和电压数据间接获得，这给soc的准确估计带来了一定的难度。

在目前的研究中，估计动力电池soc的方法主要有以下几种。闭环的估计算法，例如卡尔曼滤波算法和非线性观测器。闭环估计算法在一定程度上能提高剩余电量估计的精度，但是该方法较为复杂，并且估计soc时计算量也会加大，这就对电池管理系统有限的计算能力提出了挑战。神经网络方法，然而该方法需要大量的数据来进行学习，估计结果的好坏往往依赖于所选取的数据，一般较少被使用。最后是开路电压结合安时法估计动力电池soc，该方法操作简单方便，计算量小。电池经过长时间(2小时)的静置之后，其内部的电化学反应达到了平衡状态，此时电池的端电压等效成开路电压，结合开路电压和soc之间的关系得到当前时刻的soc，最后使用安时积分法获取其他时刻的soc。在短时间安时积分法被认为是相对准确的，然而随着估计时间的增长，由于电流的采样误差，就会造成soc累计误差的增大，因此需要经常使用开路电压法来对soc的初始值进行校正。然而，电池需要经过长时间的静置才能对初始soc进行校正，在电动汽车的实际行驶过程中，该条件往往较难被满足，尤其是对于需要长期运行的车辆，使用开路电压校准初始soc更不容易被触发。

技术实现要素：

鉴于上述问题，本发明提出了一种动力电池开路电压的估计方法，以便解决或者至少部分解决上述问题。

为了达到技术目的，本发明的技术方案是这样实现的：

本发明提供一种动力电池开路电压的估计方法，所述方法包括：

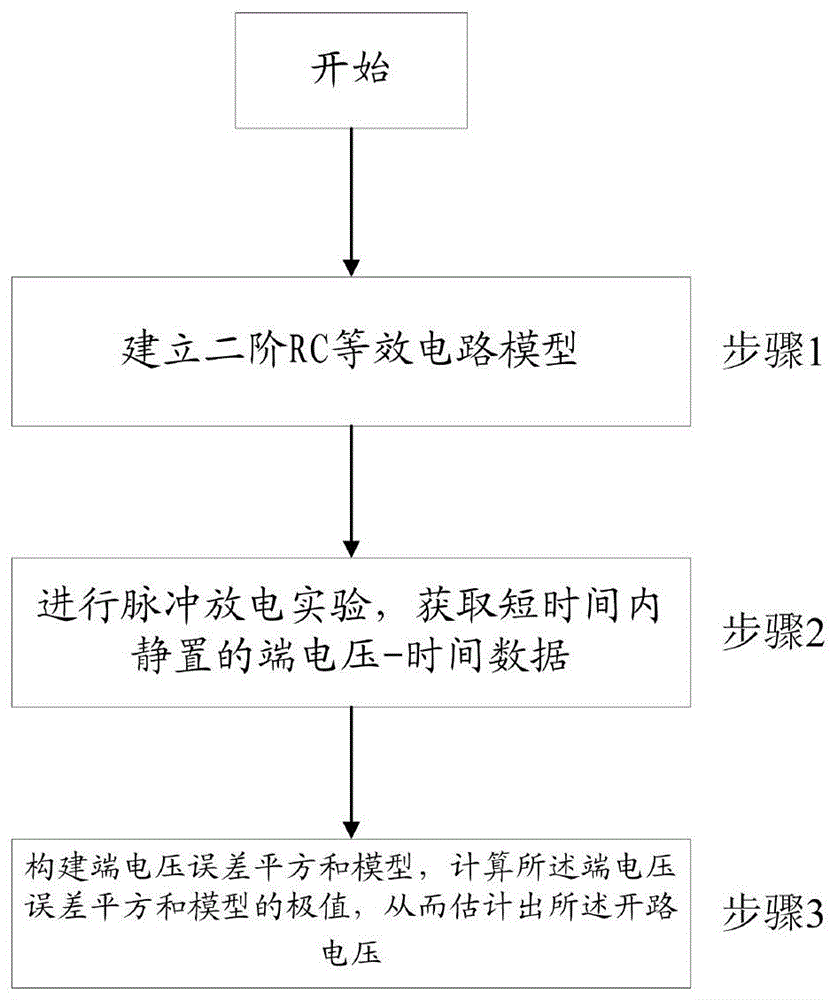
步骤1、建立二阶rc等效电路模型；

步骤2、进行脉冲放电实验，获取短时间内静置的端电压-时间数据；

步骤3、构建端电压误差平方和模型，计算所述端电压误差平方和模型的极值，从而估计出所述开路电压。

进一步的，所述建立二阶rc等效电路模型包括：

将电阻r0、r1、r2依次串联在电池包uoc的输出端，并将电容c1与电阻r1并联，电容c2与电阻r2并联；

状态方程：

输出方程：

ut＝uoc(soc)-r0it-u1-u2(2)

式(1)和式(2)中：qn是电池当前最大可用容量，uoc(soc)是关于soc的函数的当前开路电压，it是电池包的总电流，ut是电池的端电压，r0是电池的欧姆内阻，u1和u2分别是电容c1和c2两端的电压；

基于叠加原理，求得极化电压u1和u2：

式(3)和式(4)中：t是时间，u1(t)是t时刻电容c1两端的极化电压，u1(0)是初始时刻电容c1两端的极化电压，u2(t)是t时刻电容c2两端的极化电压，u2(0)是初始时刻电容c2两端的极化电压，it是电池包的总电流，τ1是电容c1与电阻r1的乘积，τ2是电容c2与电阻r2的乘积；

令从t＝0时起电流为0，则在t时刻的极化电压u1和u2可以表示为：

则电池的端电压ut(t)可表示为：

则式(7)可表示为：

f(a,b,c)＝ax+by+c(8)

其中，f(a,b,c)＝ut(t)，a＝u1(0)，b＝u2(0)，c＝uoc(soc)。

进一步的，通过上述脉冲测量的结果，可以获得上述x、y的值。

进一步的，所述利用离线最小二乘法估计所述开路电压包括：

步骤301、构建端电压误差平方和模型：

式(9)中：rss是端电压误差平方和，zi是在i时刻的测量得到的端电压值，xi是在i时刻x的取值，yi是在i时刻y的取值；

步骤302、求所述端电压误差平方和模型极值：

对所述端电压误差平方和模型中的a,b,c一阶偏导；

令上述一阶偏导数等于零，则有：

令则式(11)可简化为：

假设在(a0,b0,c0)点上，式(12)成立；

对所述端电压误差平方和模型中的a,b,c二阶偏导；

从式(13)可以看出各项二阶偏导数均大于零，又因所述rss在(a0,b0,c0)点对于a,b,c的一阶偏导数为0，则所述rss在(a0,b0,c0)点为最小值。

步骤303、估计所述开路电压：

在所述rss取最小值时的c0为所述开路电压，则有：

即得到所述开路电压的值。

本发明的有益效果是：

本发明基于二阶rc等效电路模型，利用一段较短静置时间的端电压-时间的数据，并结合最小二乘法，能够在较短的时间内估计得到准确的开路电压。

上述说明仅是本申请技术方案的概述，为了能够更清楚了解本申请的技术手段，而可依照说明书的内容予以实施，并且为了让本申请的上述和其它目的、特征和优点能够更明显易懂，以下特举本申请的具体实施方式。

附图说明

通过阅读下文优选实施方式的详细描述，各种其他的优点和益处对于本领域普通技术人员将变得清楚明了。附图仅用于示出优选实施方式的目的，而并不认为是对本申请的限制。在附图中：

图1示出了本发明提供开路电压估计方法的系统框图；

图2示出了本发明中二阶rc等效电路模型简图；

图3示出了本发明一个实施例中静置一段时间内的端电压-时间数据图；

图4示出了本发明一个实施例中使用该方法估计得到的开路电压和真实开路电压对比图；

图5示出了本发明一个实施例中使用该方法估计得到的开路电压的误差图；

图6示出了本发明一个实施例中使用该方法估计得到的开路电压误差的放大图。

具体实施方式

下面将参照附图更详细地描述本申请的示例性实施例。虽然附图中显示了本申请的示例性实施例，然而应当理解，可以以各种形式实现本申请而不应被这里阐述的实施例所限制。相反，提供这些实施例是为了能够更透彻地理解本申请，并且能够将本申请的范围完整的传达给本领域的技术人员。

本发明实施例公开一种动力电池开路电压的估计方法，该方法包括：

步骤1、建立二阶rc等效电路模型；

步骤2、进行脉冲放电实验，获取短时间内静置的端电压-时间数据；

步骤3、构建端电压误差平方和模型，计算所述端电压误差平方和模型的极值，从而估计出所述开路电压。

如图1所示，在本发明中，二阶rc等效电路模型可以很好的描述锂电池的动态特性，基于二阶rc等效电路模型，利用离线参数辨识方法对模型参数进行辨识，根据建立的模型得到端电压方程表达式；然后利用静置阶段后一段时间的端电压-时间数据来对开路电压进行拟合，进而能够在较短的时间内估计得到准确的开路电压。从图3可以看出，电池经过很长时间静置后，端电压才能趋于稳定，此时的端电压才能等效成开路电压。从图4、图5和图6可以看出，利用本发明来估计开路电压，在短时间内就实现估计，并且估计值和真实值基本一致。

在一个实施例中，建立二阶rc等效电路模型包括：

如图2所示，将电阻r0、r1、r2依次串联在电池包uoc的输出端，并将电容c1与电阻r1并联，电容c2与电阻r2并联；

状态方程：

输出方程：

ut＝uoc(soc)-r0it-u1-u2(2)

式(1)和式(2)中：qn是电池当前最大可用容量，uoc(soc)是关于soc的函数的当前开路电压，it是电池包的总电流，ut是电池的端电压，r0是电池的欧姆内阻，u1和u2分别是电容c1和c2两端的电压；

基于叠加原理，求得极化电压u1和u2：

式(3)和式(4)中：t是时间，u1(t)是t时刻电容c1两端的极化电压，u1(0)是初始时刻电容c1两端的极化电压，u2(t)是t时刻电容c2两端的极化电压，u2(0)是初始时刻电容c2两端的极化电压，it是电池包的总电流，τ1是电容c1与电阻r1的乘积，τ2是电容c2与电阻r2的乘积；

令从t＝0时起电流为0，则在t时刻的极化电压u1和u2可以表示为：

则电池的端电压ut(t)可表示为：

则式(7)可表示为：

f(a,b,c)＝ax+by+c(8)

其中，f(a,b,c)＝ut(t)，a＝u1(0)，b＝u2(0)，c＝uoc(soc)。

在一个实施例中，根据端电压-时间数据，计算各离散的xi、yi值。

在一个优选实施例中，利用短时间内静置的端电压-时间数据估计开路电压包括：

步骤301、构建端电压误差平方和模型：

式(9)中：rss是端电压误差平方和，zi是在i时刻的测量得到的端电压值，xi是在i时刻x的取值，yi是在i时刻y的取值；

步骤302、求端电压误差平方和模型极值：

对端电压误差平方和模型中的a,b,c一阶偏导；

令上述一阶偏导数等于零，则有：

令则式(11)可简化为：

假设在(a0,b0,c0)点上，式(12)成立；

对端电压误差平方和模型中的a,b,c二阶偏导；

从式(13)可以看出各项二阶偏导数均大于零，又因rss在(a0,b0,c0)点对于a,b,c的一阶偏导数为0，则rss在(a0,b0,c0)点为最小值。

步骤303、估计开路电压：

在rss取最小值时的c0为开路电压，则有：

代入短时间内静置的端电压-时间数据，计算出开路电压的值。

综上，本发明公开了一种开路电压的估计方法，该方法包括：首先、建立二阶rc等效电路模型；其次、进行脉冲放电实验，获取短时间内静置的端电压-时间数据；再次、构建端电压误差平方和模型，计算所述端电压误差平方和模型的极值，从而估计所述开路电压。本发明能够在较短时间内估计得到准确的开路电压，对安时积分法中soc的初始值校正更加频繁，弥补了安时积分法累积误差随时间增大的缺点，提高了soc估计算法的鲁棒性。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到变化、替换或改进，都应涵盖在本发明的保护范围之内。

在此处所提供的说明书中，说明了大量具体细节。然而，能够理解，本申请的实施例可以在没有这些具体细节的情况下实践。在一些实例中，并未详细示出公知的方法、结构和技术，以便不模糊对本说明书的理解。