基于改进3D-ESPRIT算法的散射中心模型参数估计方法与流程

本发明涉及基于几何绕射理论(gtd，geometrictheoryofdiffraction)散射中心模型参数估计提取技术，具体涉及利用一种改进的3d-esprit(three-dimensionalestimatingsignalparameterviarotationalinvariancetechniques)算法，即基于一种改进3d-esprit算法的散射中心模型参数估计方法。

背景技术：

一、散射中心发展简介

目前，基于几何绕射理论(gtd，geometrictheoryofdiffraction)的散射中心模型已成为雷达目标电磁散射数据的有效表述模型之一(potterlc，chiangdm，carrierer.agtd-basedparametricmodelforradarscattering[j].ieeetransactiononantennasandpropagation，1995，43(10)：1058-1066.)。gtd散射中心模型的核心机理为：雷达目标在高频区的电磁散射回波可近似等效为有限个强散射中心的相干叠加合成的。gtd散射中心模型作为描述目标电磁散射特性的经典模型，在雷达目标识别(1、dingby，wengj.aregionmatchingapproachbasedon3dscatteringcentermodelwithapplicationtosartargetrecognition[j].ieeesensorsjournal，2018，18(11)：4623-4632.2、litl，dul.sarautomatictargetrecognitionbasedonattributescatteringcentermodelanddiscriminativedictionarylearning[j].ieeesensorsjournal，2019，19(12)：4598-4611.3、zhoujx，shizg，chengx，etal.automatictargetrecognitionofsarimagesbasedonglobalscatteringcentermodel[j].ieeetransongeoscienceandremotesensing，2011，19(10)：3713-3729.)，rcs频率内插与外推(1、邱志强.基于空间谱估计的雷达目标散射中心提取研究[d].成都：电子科技大学，2016.2、钟金荣.目标三维电磁散射参数化模型反演方法研究[d].长沙：国防科学技术大学，2016.)，雷达目标三维重构等军事领域均有着十分广泛的应用前景(zhaoy，zhangl，jiub，etal.three-dimensionalreconstructionforspacetargetswithmultistaticinversesyntheticapertureradarsystems[j].eurasipjournalonadvancesinsignalprocessing，2019：2019(40).)。

而如何通过雷达目标的电磁散射回波数据准确估计出gtd散射中心模型参数，从而构建精准的散射中心模型，对雷达目标电磁散射特性的刻画显得尤为重要。针对此类模型参数估计问题，国内外研究者利用如music算法(1、王旭东，仲倩，闫贺，等.一种二维信号波达方向估计的改进多重信号分类算法[j].电子与信息学报，2019，41(9)：2137-2142.2、郑舒予，张小宽，宗彬锋.基于改进music算法的散射中心参数提取及rcs重构[j].系统工程与电子技术，2020，42(01)：76-82.3、tanj，niezp.polarizationsmoothinggeneralizedmusicalgorithmwithpolarizationsensitivearrayforlowangleestimation[j].sensors，2018，18(5)：1534-1549.)、esprit算法(1、leymens，konstantinu，pierrec.multidimensionalespritfordampedandundampedsignals：algorithm，computations，andperturbationanalysis[j].ieeetrans.onsignalprocessing，2017，65：5897-5910.2、zhangw，zhangxf，sunhp，etal.non-circulargeneralised-espritalgorithmfordirectionofarrivalestimation[j].ietradar，sonar&navigation，2017，11(5)：736-744.)等对参数进行估计提取。

gtd散射中心模型从维度的角度可分为一维、二维及三维模型。随着维度的增大，gtd散射中心模型对目标电磁散射特性刻画得愈加精准，但算法的运算复杂度也随之增加。目前多数研究者主要针对一维gtd散射中心模型、二维gtd散射中心模型进行参数估计提取，对三维gtd散射中心模型参数估计问题涉及甚少。对此本发明利用经典3d-esprit算法对三维gtd散射中心模型进行参数估计提取。

经典3d-esprit算法可较为准确地估计得到三维gtd散射中心模型参数，但当外界环境的噪声较高时，算法的参数估计性能会显著降低。为解决这一问题，本发明提出一种基于平方前后向平滑的3d-esprit(p-fb-3d-esprit)算法，该改进算法可有效提高算法的噪声鲁棒性与参数估计性能。

二、gtd散射中心模型简介(本发明依托的基本模型)

gtd散射中心模型作为一种经典的散射中心模型，可有效描述雷达目标在高频区的电磁后向散射特性，以步进频率雷达信号为例，目标的三维gtd散射中心模型可表示如下(温晓杨，石志广，赵宏钟，等.一种基于3d-esprit的散射中心参数估计算法[j].雷达科学与技术，2007，5(2)：119-123.)：

式中，表示目标的后向散射回波，分别表示变化的频率、方位角、俯仰角，分别表示目标的方位角和俯仰角。i代表散射中心个数，{ai，αi，xi，yi，zi}分别表示第i个散射中心的散射强度、散射类型、横向距离、纵向距离及垂直距离。fm＝f0+mδf，m＝0，1，...，m1，...，m，其中f0为起始频率，δf为步进频率，m代表频率下标，m为总频率步进数；θn＝θ0+nδθ，n＝0，1，...，n1，...，n，其中θ0为起始方位角，δθ为步进方位角，n为方位角下标，n为总方位角步进数；其中为起始俯仰角，为步进俯仰角，k为俯仰角下标，k为总俯仰角步进数；nδθ、分别为方位方向上的小转角、俯仰方向上的小转角。c＝3×10⁸m/s为电磁波传播速度，为复高斯白噪声。αi为0.5的整数倍，共有5种，不同散射体对应不同的αi值(王菁.光学区雷达目标散射中心提取及其应用研究[d].南京：南京航空航天大学，2010.)，见表1。

表1典型散射结构的αi取值

由于选择的雷达工作频率满足δf/f0＜＜1，因此可作如下近似：

将式(2)中的近似结果带入式(1)，将得到的公式变换到笛卡尔坐标并进行插值规范化处理、利用重采样技术(坐标变换、差值规范化处理、重采样技术是三种基本技术，为本领域技术人员所熟知，在此不再赘述)，则目标的电磁回波数据可用式(3)表示。

式中，m＝0，...，m-1，n＝0，...，n-1，k＝0，...，k-1

其中fx0、fy0、fz0分别为雷达坐标系的x、y、z方向上的雷达信号初始频率；

pyi＝exp(-4πjδfyyi/c)(6)

pzi＝exp(-4πjδfzzi/c)(7)

其中δfx、δfy、δfz分别代表雷达坐标系下x、y、z方向的步进频率，表达式如式(8)所示：

设fc为雷达的中心频率，b为雷达工作带宽，则：

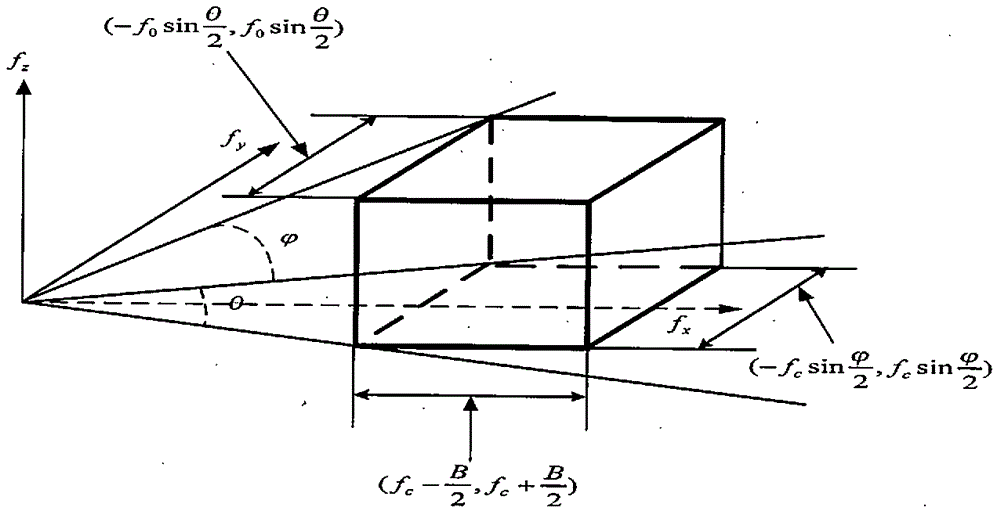
图1表示三维频域数据范围，图中立方体内包含了插值后的等间隔数据点。

式(5)-(7)包含散射中心的类型参数及三类位置参数，因此可由下式(12)-(14)求解：

αi＝(|pxi|-1)f0/δf(12)

其中δfx、δfy、δfz分别表示分别代表雷达坐标系的x、y、z方向上的步进频率；angle(.)表示matlab中求复数的相角函数。

技术实现要素：

为进一步提高对目标回波数据的利用，本发明提出一种基于改进3d-esprit(pq-fb-3d-esprit)算法的散射中心模型参数估计方法，包括下列步骤：

第一步：获取目标极化电磁散射数据

首先，在原始三维gtd散射中心模型的基础上，增加对目标极化信息的利用，将极化散射系数si，p加入三维gtd散射中心模型之中，得到全极化三维gtd散射中心模型如下：

式中，表示目标的后向散射回波，分别表示变化的频率、方位角、俯仰角：fm＝f0+mδf，m＝0，1，...，m，f0为起始频率，δf为步进频率，m代表频率下标，m为总频率步进数；θn＝θ0+nδθ，n＝0，1，...，n，其中θ0为起始方位角，δθ为步进方位角，n为方位角下标，n为总方位角步进数；其中为起始俯仰角，为步进俯仰角，k为俯仰角下标，k为总俯仰角步进数；nδθ、分别为方位方向上的小转角、俯仰方向上的小转角；i代表散射中心个数；si，p表示第i个散射中心在p极化方式下的散射系数，p∈{hh，hv，vh，vv}表示四种极化方式：hh表示水平发射，水平接收；hv表示水平发射，垂直接收；vh表示垂直发射，水平接收；vv表示垂直发射，垂直接收；bi表示第一过渡参数；pxi、pyi、pzi分别表示第二、三、四过渡参数，这四个参数仅用于对进行拆分，便于后续参数估计；{xi，yi，zi}分别表示第i个散射中心的横向距离、纵向距离及垂直距离；为复高斯白噪声；

下表1给出一些典型目标的散射矩阵；

表1典型目标的散射矩阵

第二步：建立汉克尔hankel矩阵

首先基于目标后向电磁数据构建hankel矩阵；

先沿雷达坐标系x方向进行平滑，构建一个[p×q×l]×[(m-p+1)×(n-q+1)×(k-l+1)]的增强矩阵x^x，如下式(17)所示；其中m、n、k定义同式(1)，m/2≤p≤2m/3、n/2≤q≤2n/3、k/2≤l≤2k/3，p、q、l均为在上述范围内取值的过程变量；

式中，

对含有极化信息的矩阵进行前后向空间平滑处理，可得到新的总协方差矩阵r，如式(20)：

式中，代表矩阵x^x的自相关协方差矩阵；代表矩阵x^x和矩阵y的互相关协方差矩阵；y＝jx^x；为一个维度为(p×q×l)×(p×q×l)的置换矩阵，其反对角线元素为1其余位置上元素为0；

第三步：平方处理

由式(20)可知，总协方差矩阵r为埃尔米特hermittan矩阵，因此其满足r＝r^h，即r1＝rr^h＝r²；则平方后得到的矩阵r1、总协方差矩阵r两者特征值与特征向量具有以下关系式：

式中，λ1、λ分别代表平方后得到的矩阵r1与总协方差r的特征值，λ1、λ分别代表平方后得到的矩阵r1与总协方差r的特征向量；

用平方后得到的r1代替总协方差矩阵r，能够增大信号特征值与噪声特征值之间的差距，并且不会改变原有的特征向量，因此在信噪比较低时，更容易区分信号特征值与噪声特征值；从数学关系上来看，各参数的方差表示如下：

式中，e{·}为方差，ω分别代表第i次蒙特卡洛实验估计得到的参数及原始参数；σ²、γi分别代表噪声对应的特征值和信号对应的特征值；i代表总散射中心数目；vi代表第i个特征值γi对应的特征矩阵；(vi)^h代表vi的转置矩阵；vi＝γie-x^x；e代表维度为[p×q×l]×[p×q×l]的单位矩阵；g^h是g的转置矩阵；

g＝[ai，...，ai](23)

式中，c＝3×10⁸m/s为电磁波传播速度，αi表示第i个散射中心的散射类型；

则由式(22)知，增大噪声特征值与信号特征值之间的差距，方差会减小，能够达到减小估计参数的方差的作用；因此，构建下式(26)的平方后得到的最终总协方差矩阵r1，用以代替总协方差矩阵r，能够等效为增大了信噪比，有效提高参数的估计精度；

r1＝rr^h＝r²(26)

第四步：奇异值分解

对增强矩阵x^x作奇异值分解，得到式(27)：

式中：uxs、vxs均代表雷达坐标系x方向的信号特征值向量，分别由x^x的前i个主左特征向量与前i个主右特征向量构成；其中uxn，vxn代表x^x的噪声子空间，分别由x^x的非主左特征向量与非主右特征向量构成；dxs为信号特征值构成的对角矩阵；dxn为噪声特征值构成的对角矩阵；

第五步：构造过程矩阵fx

构造过程矩阵fx如下：

式中，uxs，分别为矩阵uxs去除后q×l行、去除前q×l行得到的矩阵，代表uxs的广义逆矩阵；

第六步：利用前文中的置换矩阵j求得雷达坐标系y方向、z方向对应的信号子空间

三维条件下的置换矩阵exy，eyz，exz如下：

式中，表示克罗内克(kronecker)乘积，代表(q，l)位置上元素为1，其他位置上元素为0的q×l矩阵，代表(l，p)位置上元素为1，其他位置上元素为0的l×p矩阵，代表(p，q)位置上元素为1，其他位置上元素为0的p×q矩阵；

根据三个方向上增广矩阵exy、eyz、exz之间的关系，得到雷达坐标系不同方向上的信号子空间之间关系式如下：

uys＝exyuxs(32)

uzs＝eyzuys(33)

uxs＝exzuzs(34)

式中，uys代表雷达坐标系y方向的信号特征值向量；uzs代表雷达坐标系z方向的信号特征向量；

因此，根据式(27)求得的uxs及式(32)-(33)，可得到uys和uzs，进而可得到雷达坐标系y方向、z方向的过程矩阵fy、fz，两者的表达式如下：

式中，uys，分别为矩阵uys去除后q×l行、去除前q×l行得到的矩阵；uzs，分别为矩阵uzs去除后q×l行、去除前q×l行得到的矩阵；分别代表uys和uzs的广义逆矩阵；

第七步：计算主特征值向量及其对应元素

首先根据下式(37)-(39)计算过程矩阵fx、fy、fz前i个元素的主特征值向量ψx、ψy、ψz；

式中，tx、ty、tz均为非奇异矩阵，也就是说，tx、ty、tz只要是非奇异矩阵即可；

基于此求解pxi、pyi、pzi与类型参数αi及三类位置参数xi、yi、zi：由式(40)-(42)求得的矩阵ψx、ψy、ψz主对角线上的元素对应为pxi，pyi，pzi：

pxi＝diag(ψx)，i＝1，...，i(40)

pyi＝diag(ψy)，i＝1，...，i(41)

pzi＝diag(ψz)，i＝1，...，i(42)

根据式(40)-(42)求得的pxi，pyi，pzi，将其带回到式(12)-(15)

αi＝(|pxi|-1)f0/δf(12)

求解类型参数αi，横向距离参数xi、纵向距离参数yi与垂直距离参数zi；δfx、δfy，、δfz分别表示分别代表雷达坐标系的x、y、z方向上的步进频率；其中angle(.)表示matlab中求复数的相角函数；

第八步：散射强度参数求解

在估计得到类型参数与三类位置参数的基础上，利用最小二乘法对散射中心模型中的强度参数进行求解，如下所示：

式中，(g^hg)^-1代表矩阵g^hg的共轭转置；es为目标散射回波数据构成的过程矩阵，es的表达式如式(44)所示，

本发明的方法首先将目标的极化信息以极化散射矩阵的方式加到三维gtd散射中心模型中，其次对协方差矩阵进行前后向平滑处理，最后对总协方差矩阵取平方处理。该方法有效延长可利用目标电磁散射回波数据的长度，能够进一步提高算法的参数估计性能与噪声鲁棒性。

附图说明

图1示出三维频域数据范围示意图；

图2示出不同算法，gtd散射中心模型各参数平均均方差比较，其中图2(a)示出横向距离x的平均均方差比较，图2(b)示出纵向距离y的平均均方差比较，图2(c)示出垂直距离z的平均均方差比较，图2(d)示出散射类型α的平均均方差比较，图2(e)示出强度a的平均均方差比较；

图3示出snr＝0db，不同算法的定位精度比较；

图4示出snr＝10db，不同算法的定位精度比较。

具体实施方式

下面结合附图和实施例对本发明进一步说明，本发明包括但不仅限于下述实施例。

一.改进算法的原理

本发明提出一种改进的3d-esprit算法，有效地利用目标极化散射信息，从而提高了算法的参数估计性能，包括下列步骤：

第一步：获取目标极化电磁散射数据。

首先，在原始三维gtd散射中心模型的基础上，增加对目标极化信息的利用，将极化散射系数si，p加入三维gtd散射中心模型之中，可得全极化三维gtd散射中心模型如下：

式中，si，p表示第i个散射中心在p极化方式下的散射系数；p∈{hh，hv，vh，vv}表示四种极化方式：hh表示水平发射，水平接收；hv表示水平发射，垂直接收；vh表示垂直发射，水平接收；vv表示垂直发射，垂直接收。bi表示第一过渡参数；pxi、pyi、pzi分别表示第二、三、四过渡参数，这四个参数仅用于对进行拆分，便于后续参数估计。下表1给出一些典型目标的散射矩阵。

第二步：建立汉克尔(hankel)矩阵。

为更为准确地估计散射中心模型参数，首先要对目标的后向电磁散射数据进行空间平滑处理以去相关，而hankel矩阵可替代空间平滑起到去相关的作用。因此，首先基于目标后向电磁数据构建hankel矩阵。

先沿图1中雷达坐标系x方向进行平滑，构建一个[p×q×l]×[(m-p+1)×(n-q+1)×(k-l+1)]的增强矩阵x^x，如下式(17)所示。其中m、n、k定义同式(1)，m/2≤p≤2m/3、n/2≤q≤2n/3、k/2≤l≤2k/3，p、q、l均为在上述范围内取值的过程变量。

表1典型目标的散射矩阵

式中，

对含有极化信息的矩阵进行前后向空间平滑处理，可得到新的总协方差矩阵r，如式(20)：

式中，代表矩阵x^x的自相关协方差矩阵；代表矩阵x^x和矩阵y的互相关协方差矩阵；y＝jx^x；为一个维度为(p×q×l)×(p×q×l)的置换矩阵，其反对角线元素为1其余位置上元素为0；x^x、p、q、l定义均同前文。

第三步：平方处理。

由式(20)可知，总协方差矩阵r为埃尔米特(hermittan)矩阵，因此其满足r＝r^h，即r1＝rr^h＝r²。则平方后得到的矩阵r1、总协方差矩阵r两者特征值与特征向量具有以下关系式：

式中，λ1、λ分别代表平方后得到的矩阵r1与总协方差r的特征值，λ1、λ分别代表平方后得到的矩阵r1与总协方差r的特征向量。

用平方后得到的r1代替总协方差矩阵r，可增大信号特征值与噪声特征值之间的差距，并且不会改变原有的特征向量，因此在信噪比较低时，可更容易区分信号特征值与噪声特征值。从数学关系上来看，各参数的方差可表示如下：

式中，e{·}为方差，分别代表第i次蒙特卡洛实验本发明估计得到的参数及原始参数；σ²、γi分别代表噪声对应的特征值和信号对应的特征值；m、n、k定义同式(1)；i代表总散射中心数目；vi代表第i个特征值γi对应的特征矩阵；(vi)^h代表vi的转置矩阵；vi＝γie-x^x；e代表维度为[p×q×l]×[p×q×l]的单位矩阵；p、q、l定义均同前文，g^h是g的转置矩阵。

g＝[a1，...，ai](23)

式中，c＝3×10⁸m/s为电磁波传播速度，αi表示第i个散射中心的散射类型。

则由式(22)可知，增大噪声特征值与信号特征值之间的差距，方差会减小，即可达到减小估计参数的方差的作用。因此，构建下式(26)的平方后得到的最终总协方差矩阵r1，用以代替总协方差矩阵r，可等效为增大了信噪比，有效提高参数的估计精度。

r1＝rr^h＝r²(26)

第四步：奇异值分解。

对增强矩阵x^x作奇异值分解，得到式(27)：

式中：uxs、vxs均代表雷达坐标系x方向的信号特征值向量，分别由x^x的前i个主左特征向量与前i个主右特征向量构成；其中uxn，vxn代表x^x的噪声子空间，分别由x^x的非主左特征向量与非主右特征向量构成；dxs为信号特征值构成的对角矩阵；dxn为噪声特征值构成的对角矩阵；i为总散射中心数目。

第五步：构造过程矩阵fx。

构造过程矩阵fx如下：

式中，uxs，分别为矩阵uxs去除后q×l行、去除前q×l行得到的矩阵，代表uxs的广义逆矩阵。

第六步：利用前文中的置换矩阵j求得雷达坐标系y方向、z方向对应的信号子空间。

由文献(王菁.光学区雷达目标散射中心提取及其应用研究[d].南京：南京航空航天大学，2010.)可推导出三维条件下的置换矩阵exy，eyz，exz如下：

式中，表示克罗内克(kronecker)乘积，代表(q，l)位置上元素为1，其他位置上元素为0的q×l矩阵，代表(l，p)位置上元素为1，其他位置上元素为0的l×p矩阵，代表(p，q)位置上元素为1，其他位置上元素为0的p×q矩阵。

根据三个方向上增广矩阵exy、eyz、exz之间的关系，可得到雷达坐标系不同方向上的信号子空间之间关系式如下：

uys＝exyuxs(32)

uzs＝eyzuys(33)

uxs＝exzuzs(34)

式中，uys代表雷达坐标系y方向的信号特征值向量；uzs代表雷达坐标系z方向的信号特征向量。

因此，根据式(27)求得的uxs及式(32)-(33)，可得到uys和uzs，进而可得到雷达坐标系y方向、z方向的过程矩阵fy、fz，两者的表达式如下：

式中，uys，分别为矩阵uys去除后q×l行、去除前q×l行得到的矩阵；uzs，分别为矩阵uzs去除后q×l行、去除前q×l行得到的矩阵；分别代表uys和uzs的广义逆矩阵；q、l定义均同前文。

第七步：计算主特征值向量及其对应元素。

首先根据下式(37)-(39)计算过程矩阵fx、fy、fz前i个元素的主特征值向量ψx、ψy、ψz。

式中，tx、ty、tz均为非奇异矩阵，也就是说，tx、ty、tz只要是非奇异矩阵即可。

基于此求解pxi、pyi、pzi与类型参数αi及三类位置参数xi、yi、zi：由式(40)-(42)求得的矩阵ψx、ψy、ψz主对角线上的元素对应为pxi，pyi，pzi，即：

pxi＝diag(ψx)，i＝1，...，i(40)

pyi＝diag(ψy)，i＝1，...，i(41)

pzi＝diag(ψz)，i＝1，...，i(42)

根据式(40)-(42)求得的pxi，pyi，pzi，并将其带回到式(12)-(15)，可求解类型参数，横向距离参数、纵向距离参数与垂直距离参数。

第八步：散射强度参数求解。

在估计得到类型参数与三类位置参数的基础上，利用最小二乘法(张贤达.现代信号处理[m].北京：清华大学出版社，2002.)，可对散射中心模型中的强度参数进行求解，如下所示：

式中，g定义同式(23)；g^h代表g的转置，(g^hg)^-1代表矩阵g^hg的共轭转置；es为目标散射回波数据构成的过程矩阵，下标s代表英文scattering的首字母，es的表达式如式(44)所示，

式中，p、q、l定义均同前文。

二.仿真实验分析

仿真实验1：平均均方差比较。由于文章篇幅限制，分别在信噪比为-10db～20db，每个信噪比下进行200次蒙特卡洛实验并比较不同算法估计得到各参数，并比较其平均均方差(mean-root-mean-errors，mrmse)，使得本发明内容更加精炼。仿真结果如图2所示。其中，定义平均均方差mrmse如下：

式中，表示第i次仿真实验估计得到的散射中心参数，ω表示真实设定的散射中心参数，d表示每个信噪比对应的蒙特卡洛实验次数，i为总散射中心个数。

由图2中的(a)-(e)可知，相比与经典3d-esprit算法，q-fb-3d-esprit算法的均方差要略低，参数估计精度较高，而改进算法的各散射中心模型参数的平均均方差均小于经典3d-esprit算法及q-fb-3d-esprit算法，且在低信噪比-10db-0db的仿真条件下优势更为明显；且随着信噪比的增大，三种算法的参数估计精度随之提高并趋于一致。仿真实验验证了本发明改进算法的有效性与先进性，即通过对目标极化信息的利用可延长电磁散射数据的长度，并有效提高了算法的噪声鲁棒性与参数估计性能。

仿真实验2：为进一步验证本发明算法的有效性与先进性，在信噪比为0db及10db仿真条件下，每个信噪比对应200次蒙特卡洛实验，分别利用经典3d-esprit算法、改进q-fb-3d-esprit算法和本发明改进的pq-fb-3d-esprit算法对四个散射中心位置进行定位并加以比较。

由图3可知，在信噪比为0db条件下，经典3d-esprit算法对四个散射中心均无法准确定位；q-fb-3d-esprit算法可准确定位其中三个散射中心，而对另一个散射中心的定位则稍有偏差；而本发明提出的改进pq-fb-3d-esprit算法对四个散射中心的位置均能准确定位。由图4可知，在信噪比为10db条件下，经典3d-esprit算法亦无法准确定位四个散射中心的位置；而q-fb-3d-esprit算法与本发明改进算法均可准确定位四个散射中心的位置。从上述两个仿真实验可得，经典3d-esprit算法的参数估计性能与在噪声鲁棒性最差，而提出的改进算法的参数估计性能与噪声鲁棒性最好，进而验证了提出改进算法的有效性与优越性。本发明提出一种改进的3d-esprit算法，有效提高了gtd散射中心模型参数估计精度，本发明中改进算法的优越性主要表现在以下两个方面：

1.提出的改进算法增加了对目标极化散射信息的利用，有效地延长了可利用数据的长度信息，从而大大提高了目标电磁散射数据的利用率；

2.提出的改进算法通过对协方差矩阵作取平方、双向平滑处理，削弱了噪声对算法参数估计性能的影响，有效地改善了算法的噪声鲁棒性。