一种多频率点雷达测速方法与流程

[0001]
本发明涉及雷达测速技术领域，尤其涉及一种多频率点雷达多普勒高精度测速方法。


背景技术：

[0002]
雷达测速主要是利用多普勒效应(doppler effect)原理：当目标向着雷达天线靠近时，反射信号频率将高于发射机频率；反之，当目标远离雷达天线而去时，反射信号频率将低于发射机频率。因此可以由频率改变的数值计算出目标与雷达的相对速度。当目标面向雷达天线运动时，多普勒频率为正，当目标背向雷达天线运动时，多普勒频率为负。
[0003]
常用的测速雷达为多普勒雷达(pulse doppler radar，简称pd雷达)，多普勒雷达根据发射信号的不同分为脉冲式(pulse wave，简称pw)多普勒雷达和连续波(continuous wave，简称cw)多普勒雷达两种。脉冲式多普勒雷达测速通过反射回来的信号中获得速度和距离等信息，一般用于军事领域。对于只需要速度信息的应用，可以使用成本低、结构简单的连续波多普勒雷达，其信号处理也十分简单，只需要考虑提取信号的频率，信号的幅度和相位等其他信息则不需要考虑。
[0004]
采用多普勒雷达测速方法可以提高测速精度，但目前技术中仍无法消除速度的多普勒测量误差。


技术实现要素：

[0005]
本发明提出了一种多频率点雷达测速方法，雷达发射不同载频频率的信号对目标进行照射，由目标反射形成回波信号，通过联合多个载频频率的回波信号可以有效消除多普勒测量误差，从而获得较高精度的速度测量值。
[0006]
为了达到上述目的，本发明提出了一种多频率点雷达测速方法，具体包含以下步骤：
[0007]
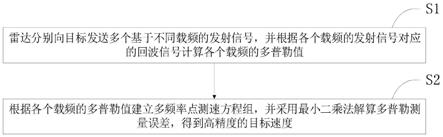
雷达分别向目标发送多个基于不同载频的发射信号，并根据各个载频的发射信号对应的回波信号计算各个载频多普勒值；
[0008]
根据各个载频的多普勒值建立多频率点测速方程组，并采用最小二乘法解算多普勒测量误差，得到高精度的目标速度。
[0009]
优选地，所述雷达的发射信号的载频的频率点数目不小于两个，且所述多个载频的频率间具有一定的差异性。
[0010]
优选地，每个载频的发射信号包括多个子信号，每个载频的发射信号对应有多个与子信号数量相同的回波信号；每个载频中，分别计算各个回波信号的傅里叶变换结果，并将其中数值最大的傅里叶变换结果所对应的频率作为该载频的多普勒值。
[0011]
优选地，根据各个载频的多普勒值建立多频率点测速方程组，包括：根据各个载频的多普勒值建立各个载频的多普勒测速方程，并联合各个载频的多普勒测速方程形成多频率点测速方程组，所述多频率点测速方程组为：
[0012][0013]
式中，f
i
为雷达发射信号的载频频率，i＝1，2，3，
…
，n，v为雷达以载频f1发射信号时所测量的速度值，δv
i1
为雷达以载频f
i
发射信号时所测量的速度值与雷达以载频f1发射信号时所测量的速度值的偏差，f
di
为雷达以载频f
i
发射信号时的多普勒值，δf
di
为雷达以载频f
i
发射信号时的多普勒误差；
[0014]
通过解算上述多频率点测速方程组可得到消除多普勒误差后的目标速度v，及多普勒误差δf
d
。
[0015]
优选地，所述多频率点测速方程组满足边界条件，所述边界条件为：各个载频的频率间具有一定的差异；不同载频的多普勒误差变化不明显，即：
[0016]
δf
d1
≈δf
d2
≈
…
≈δf
di
≈
…
≈δf
dn
＝δf
d
。
[0017]
优选地，根据所述边界条件近似变化所述多频率点测速方程组，将近似变换后的多频率点测速方程组转化为矩阵形式，并采用最小二乘法解算得到目标速度及多普勒误差；
[0018]
所述近似变换后的多频率点测速方程组的矩阵形式为：
[0019]
ax＝y
[0020]
其中，矩阵a、矩阵x和矩阵y分别表示如下：
[0021][0022]
解算得到的目标速度为：
[0023][0024]
多普勒误差为：
[0025][0026]
本发明具有以下优势：
[0027]
本发明通过发送多个频率点的发射信号对目标速度进行测量，并联合多个频率点的多普勒测速方程进行计算，不仅可以得到消除多普勒误差的高精度目标速度，还可以得到雷达测速系统的多普勒误差，用来评估雷达测速系统的性能。同时，本发明采用多频率点测速，还具有很好的抗干扰和杂波抑制的效果。
附图说明
[0028]
图1为本发明实施例提供的一种多频率点雷达测速方法的流程图；
[0029]
图2为本发明实施例提供的雷达多频率点测速的模型示意图；
[0030]
图3为本发明实施例提供的回波信号的傅里叶变换结果示意图；
[0031]
图4为本发明实施例提供的多频率点雷达测速仿真得到的目标速度与采用常规方法雷达测速的目标速度的对比示意图；
[0032]
图5为本发明实施例提供的多频率点雷达测速仿真得到的多普勒测量误差示意图。
具体实施方式
[0033]
以下结合附图和具体实施例对本发明提出的一种多频率点雷达测速方法作进一步详细说明。根据下面说明和权利要求书，本发明的优点和特征将更清楚。需说明的是，附图均采用非常简化的形式且均使用非精准的比率，仅用以方便、明晰地辅助说明本发明实施例的目的。
[0034]
如图1所示，本发明提出了一种多频率点雷达测速方法，具体包括以下步骤：
[0035]
s1、雷达分别向目标发送多个基于不同载频的发射信号，并根据各个载频的发射信号对应的回波信号计算各个载频的多普勒值；
[0036]
具体地，雷达向目标发送多个基于不同载频的发射信号，载频的频率点数目不小于2。本实施例中，雷达向目标发送n个载频的发射信号，n≥2，各个载频频率分别为f
i
，i＝
1，2，3，
……
，n，其中，f1为第一载频，f2为第二载频，依此类推，f
n
为第n载频。各个载频之间具有一定的差异性，即发射信号的载频频率不能一样或近似一样。雷达的频率点数目以及各个频率点的数值需根据雷达系统的参数和其使用的环境设定。
[0037]
每一载频的发射信号内包括m组子信号，子信号的周期设置为prt，使得子信号的无模糊速度能够满足测速需求，所述测速需求为：v≤c/4
·
f
i
·
prt，式中，v为目标速度，c为电磁波传播速度。同一载频的发射信号的频率不变，即同一载频的发射信号内的子信号具有相同的载频频率。因此，相邻两个载频的发射信号间的时间间隔为m
×
prt。
[0038]
如图2所示为雷达多频率点测速的模型示意图，雷达向目标以周期prt发射基于第一载频f1的子信号，同时接收目标反射的回波信号，持续发送m个子信号后，完成基于第一载频f1的发射信号的发送；然后发送基于第二载频f2的发射信号，并接收第二载频f2对应的回波信号；依此类推，直至发射信号的频率点数目等于n。雷达发射n个基于不同载频的发射信号，每一载频的发射信号对应有m个回波信号，因此，雷达共接收有m
×
n个回波信号。
[0039]
雷达再根据各个载频的发射信号对应的回波信号计算各个载频对应的多普勒值。具体地，雷达分别对各个载频的m个回波信号进行下变频处理及傅里叶变换，得到每个载频的m个回波信号的傅里叶变换结果；在每个载频中，将各个回波信号的傅里叶变换结果中数值最大的傅里叶变换结果所对应的频率作为本载频的多普勒值。
[0040]
进一步地，所述回波信号的公式为：
[0041]
s
j
(t)＝a(t-τ)
·
cos[f
i
·
(t-τ)]
[0042]
式中，s
j
(t)为载频的第j个回波信号，j＝1,2,...,m，a(t)＝1，|t|≤t
p
/2；t为时域变量，t
p
为发射信号宽度，τ为回波延时。
[0043]
对回波信号进行下变频处理，得到基带信号i(t)，所述基带信号i(t)为：
[0044]
i
j
(t)＝s
j
(t)
·
cos(f
i
·
t)
[0045]
其中，cos(f
i
·
t)为与发射信号频率一致的本振信号；
[0046]
对基带信号进行傅里叶变换，得到回波信号的傅里叶变换结果：
[0047]
i
j
(f)＝fft[i
j
(t)]
[0048]
频率点的多普勒值为f
di
：
[0049]
f
di
＝argmax[i(f
j
)]。
[0050]
s2、根据各个载频的多普勒值建立多频率点测速方程组，并采用最小二乘法解算多普勒测量误差，得到高精度的目标速度。
[0051]
根据各个载频的多普勒值建立各个载频的多普勒测速方程，所述多普勒测速方程为：
[0052][0053]
式中，f
i
为雷达发射信号的载频频率，v为雷达以载频f1发射信号时所测量的速度值，δv
i1
为雷达以载频f
i
发射信号时所测量的速度值与雷达以载频f1发射信号时所测量的速度值的偏差，f
di
为雷达以载频f
i
发射信号时的多普勒值，δf
di
为雷达以载频f
i
发射信号时的多普勒误差。公式1所测得的速度v为消除多普勒误差后的高精度的目标速度v。
[0054]
联立各个载频的多普勒测速方程，形成多频率点测速方程组，所述多频率点测速方程为：
[0055][0056]
上述方程组中只有两个待求变量，分别为多普勒误差δf
d
和目标速度值v，为了保证上述方程组具有高精度其唯一的解，上述方程组需满足以下边界条件：方程组1中的每个方程相互独立，多个频率点间具有一定的差异；雷达测速时间内，不同载频测量得到的多普勒误差变化不明显，即：
[0057]
δf
d1
≈δf
d2
≈
…
≈δf
di
≈
…
≈δf
dn
＝δf
d
。
[0058]
根据上述边界条件，公式2可近似得到：
[0059][0060]
将公式3等价变换为矩阵形成：
[0061]
ax＝y
ꢀꢀꢀ
(4)
[0062]
其中，矩阵a、矩阵x和矩阵y分别表示如下：
[0063][0064]
通过数值方式解算公式4，可计算得到目标速度v及多普勒误差δf
d
。具体地，采用最小二乘法对公式4进行求解，得到：
[0065]
x＝(a
t
a)-1
a
t
y
ꢀꢀꢀ
(5)
[0066]
对公式5进行逐步求解，可解算得到x的解：
[0067]
首先计算矩阵a的转置矩阵a
t
：
[0068][0069]
计算转置矩阵a
t
与矩阵a的乘积a
t
a：
[0070][0071]
计算矩阵a
t
a的逆矩阵(a
t
a)-1
：
[0072][0073]
则，公式5中逆矩阵(a
t
a)-1
与转置矩阵a
t
的乘积为：
[0074]
[0075][0076]
最后，可求解得到矩阵x：
[0077][0078]
将公式6的结果表达成非矩阵相乘的形式，则可得到消除多普勒误差后的目标速度及多普勒误差：
[0079][0080][0081]
所述多普勒误差反映了雷达测速系统的测量精度，可用于评估雷达测速系统性能的好坏。
[0082]
仿真模拟本发明的多频率点测速方法计算目标的速度，并与传统的测速方法进行比较。仿真模拟中，雷达共发送n个频率点的发射信号，载频频率分别为f1，f2，
……
，f
n
，每个载频的发射信号内包括有m个子信号，并分别对每个载频的回波信号进行傅里叶变换处理得到对应的多普勒值。如图3所示，为其中一个载频的回波信号的傅里叶变换结果。为模拟实际情况，对各个载频的多普勒值添加随机高斯白噪声，仿真计算得到目标速度及多普勒误差。如图4所示，为采用本发明的计算方法仿真得到的目标的速度与采用常规的速测方法计算得到的目标的速度的比较图，图5为采用本发明的计算方法仿真得到的多普勒测量误差。通过仿真结果可以看出，采用常规的计算方法计算得到的目标速度与本发明测得的目
标速度存在偏差，并在本发明测得的目标速度附近随机波动，而本发明够更好的抑制多普勒误差，从而得到更高的测速精度。
[0083]
尽管本发明的内容已经通过上述优选实施例作了详细介绍，但应当认识到上述的描述不应被认为是对本发明的限制。在本领域技术人员阅读了上述内容后，对于本发明的多种修改和替代都将是显而易见的。因此，本发明的保护范围应由所附的权利要求来限定。