基于信号分辨率增强的机械智能故障诊断方法与流程

[0001]
本发明涉及机械故障诊断领域，具体涉及一种基于信号分辨率增强的机械智能故障诊断方法。


背景技术：

[0002]
在现代工业中，传统机械工业正迅速向自动化、智能化转变。为了保证机器的正常运行，各种智能故障诊断方法层出不穷。雷亚国等设计了多层堆叠dae，并对频域信号加噪，从而实现了了齿轮箱的智能故障诊断。樊薇等设计了一种基于小波基稀疏信号特征提取的轴承故障诊断系统，实现强背景噪声下轴承弱特征振动信号的有效提取。王金瑞等为了提高模型训练效率，同时解决深层神经网络在训练过程中出现的梯度消失问题，引入批标准化算法，实现了轴承振动信号的快速故障诊断。
[0003]
机械故障诊断的发展离不开大数据的支持。因此，利用生成对抗网络(gan)等深度学习算法来提高训练样本的数量成为研究热点。邵思羽等将不同标号类型的故障时域数据输入到gan中，生成一维仿真信号样本，然后将其与原始信号输入到卷积神经网络中，实现训练样本的数据增强和故障识别；wang等利用gan学习故障信号的仿真频谱，实现数据增强，并选择堆叠式自编码器(sae)进行准确的故障分类；mao等还利用gan对小样本故障类型数据进行增强，实现异步电机的故障诊断，并通过对比研究验证了该方法的有效性。
[0004]
因此，数据采集的过程变得尤为重要。采样频率越高，单位时间采集的数据点越多，越有利于我们研究和分析被测对象的内部特征，从而实现对机器的准确诊断。
[0005]
因此，高分辨率样本常被用于故障诊断研究。但是，上述方法不能提高单个样本的分辨率。


技术实现要素：

[0006]
本发明的目的是针对上述不足，提出了一种简单有效的高效亚像素全连接神经网络算法，该算法使样本的分辨率得到增强，生成更多仿真的样本特征。
[0007]
本发明具体采用如下技术方案：
[0008]
基于信号分辨率增强的机械智能故障诊断方法，包括以下步骤：
[0009]
步骤1，对原始输入样本进行全连接操作，经过隐层特征映射输出四通道的低分辨率特征，全连接神经网络层采用式(8)-(10)所示：
[0010]
f1(x
lr
；w1)＝φ(w1*x
lr
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(8)
[0011]
f2(x
lr
；w2)＝φ(w2*f1(x
lr
))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(9)
[0012]
f3(x
lr
；w3)＝φ(w3*f2(x
lr
))
ꢀꢀꢀꢀꢀꢀꢀꢀ
(10)
[0013]
其中，x
lr
为低分辨率样本，w
i
，i∈(1,2，3)为第i层网络的权重，激活函数φ为relu，第一、二和第三层全连接层分别为64、32和4通道，为了实现分辨率增强操作，将低分辨率数据x
lr
通过全连接神经层输出到亚像素全连接层；
[0014]
步骤2，通过亚像素全连接层，将四通道的低分辨率特征进行周期性的排列，最终
得到一组高分辨率特征，进而实现了样本分辨率的增强，亚像素全连接层由全连接层和元素排列构成，根据公式(11)得到全连接层输出r2(r＝2)通道与输入数据维数相同的数据，
[0015]
x
sr
＝f4(x
lr
)＝ps(w3*f2(x
lr
))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(11)
[0016]
其中，x
sr
是espfcn网络生成的高分辨率样本，ps算子能够将张量的形状由h
×
w
×
c
·
r2重新排列成rh
×
rw
×
c，ps算子的数学描述如式(12)所示：
[0017]
ps(t)
p,q
＝t
|p/r|
·
|q/r|
·
r
·
mod(q/r)+mod(p/r)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(12)
[0018]
其实质是对四通道的低分辨率特征进行周期性的排列，最终得到一组高分辨率特征；
[0019]
步骤3，使用均方误差(mse)度量真实低分辨率样本与生成的低分辨率特征的差异程度，其计算公式如下：
[0020][0021]
优选地，原始输入样本中包含的点数通过式(13)计算得到：
[0022][0023]
优选地，
[0024]
利用皮尔逊相关系数pcc评估生成样本与原始高分辨率样本之间的相似性，pcc的值越大，表示两者之间的相关性越强，pcc的计算公式如(15)所示：
[0025][0026]
其中，x表示espfcn生成的样本，y表示原始高分辨率样本，cov(
·
,
·
)是协方差，σ
x
和σ
y
分别是x和y的标准差，μ
x
和μ
y
分别是x和y的均值，e是期望，espfcn与原始高分辨率样本的pcc为0.81，说明这两类样本之间的相似性较强。
[0027]
本发明具有如下有益效果：
[0028]
本方案提出了一个有效的算法
---
高效亚像素全连接神经网络(espfcn)算法。使用sae分类网络对样本进行了故障分类的准确性测试，结果验证了espfcn在增强数据分辨率方面的有效性。
附图说明
[0029]
图1为高效亚像素全连接神经网络espcn结构；
[0030]
图2为ae的架构示意图；
[0031]
图3为sae结构示意图；
[0032]
图4为espfcn结构示意图；
[0033]
图5为三种电机轴承数据类型频谱的比较示意图；
[0034]
图6为测试准确率对比曲线图
[0035]
图7为三组电机轴承数据集的可视化结果示意图
[0036]
图8为三种数据类型的频谱的比较示意图。
具体实施方式
[0037]
下面结合附图和具体实施例对本发明的具体实施方式做进一步说明：
[0038]
espcn的网络结构如图1所示。espcn主要由卷积神经网络和亚像素卷积层组成,利用l通道卷积神经网络生成低分辨率图像，然后利用亚像素卷积层对低分辨率图像进行采样，生成高分辨率图像。卷积神经网络的第一个l-1通道描述如下:
[0039][0040]
自编码器(ae)是sae的基本组成单元，主要用于数据的特征提取和降维。如图2所示，ae的结构是一个三层前馈神经网络，包括数据输入层、隐含层和输出层。ae分为两部分，即编码器部分和解码器部分。利用编码器将输入信号映射到隐层表达式中，实现数据高维特征提取的过程。利用解码器从隐层中恢复原始输入数据，完成数据重建过程。
[0041]
假设有一个未标记的训练数据集x
n
∈r
m
×1，其中x
n
∈r
m
×1只有一个样本x
n
，编码器的过程为：
[0042][0043]
其中：w
l
,b
l
,l∈(1，l-1)为可学习权值和偏移量,w
l
是一个大小为n
l-1
×
n
l
×
k
l
×
k
l
的二维卷积张量，其中n
l
是l层的特征数,k
l
是l层的卷积核数，偏移b
l
是长度为n
l
的向量，激活函数被逐个应用并固定。经过卷积神经网络层，得到与输入图像形状相同的特征图像，并将特征图像发送到亚像素卷积层进行采样。
[0044]
亚像素卷积层由卷积层和亚像素卷积层两部分组成。卷积层部分输出与输入图像形状相同的r2个低分辨率卷积特征图，输入图像作为输出，其中r为图像的放大倍数，然后根据公式计算特征图：
[0045]
i
sr
＝f
l
(i
lr
)＝ps(w
l
*f
l-1
(i
lr
)+b
l
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0046]
其中ps是一个将元素按形状重新排列的操作符。重排ps的数学描述如下：
[0047]
ps(t)
x,y
＝t
|x/r|
·
|y/r|
·
r
·
mod(y/r)+mod(x/r)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0048]
其实质是将低分辨率的特征周期性地插入到高分辨率图像中。
[0049]
h
n
＝s
f
(wx
n
+b)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0050]
其中，h
n
表示由x
n
计算出的隐藏编码器向量，s
f
为编码器激活函数，b为偏置向量，w为权值矩阵。
[0051]
g
θ
′
是解码函数，它将h
n
从低维特征映射回高维特征，产生重构。
[0052][0053]
其中s
g
为解码器激活函数，d为偏置向量，w
t
为权值矩阵。
[0054]
对aes的参数集进行优化，使重建误差最小：
[0055][0056]
其中，aes的参数集为θ＝{w，b}和θ'＝{w
t
,d},其中b、d为偏置向量，w、w
t
为权值矩阵。
[0057]
我们选择sae作为分类模型。sae是一个三层网络的前馈神经网络，如图3所示，包括数据输入层、隐含层和输出层。输入层神经元数目与输入样本相同。隐层神经元的数目与输入样本的维数有关。输入维数为300时，隐含层神经元数为200-150-100。当输入维度为1200时，隐含层神经元数为600-200-100。输出层神经元数目与健康轴承相同。网络的激活函数为sigmoid，迭代训练次数为20次，学习率为1e-3，批量大小为5。最后一层使用softmax
分类器，采用bp算法对sae网络进行微调。需要注意的是，为了提高网络训练速度，避免梯度消失的问题，在sae的每一个激活层之前都使用了批标准化(bn)算法。
[0058]
如图4所示，基于信号分辨率增强的机械智能故障诊断方法，包括以下步骤：
[0059]
步骤1，对原始输入样本进行全连接操作，经过隐层特征映射输出四通道的低分辨率特征，全连接神经网络层采用式(8)-(10)所示：
[0060]
f1(x
lr
；w1)＝φ(w1*x
lr
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(8)
[0061]
f2(x
lr
；w2)＝φ(w2*f1(x
lr
))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(9)
[0062]
f3(x
lr
；w3)＝φ(w3*f2(x
lr
))
ꢀꢀꢀꢀꢀꢀꢀꢀ
(10)
[0063]
其中，x
lr
为低分辨率样本，w
i
，i∈(1,2，3)为第i层网络的权重，激活函数φ为relu，第一、二和第三层全连接层分别为64、32和4通道，为了实现分辨率增强操作，将低分辨率数据x
lr
通过全连接神经层输出到亚像素全连接层；
[0064]
步骤2，通过亚像素全连接层，将四通道的低分辨率特征进行周期性的排列，最终得到一组高分辨率特征，进而实现了样本分辨率的增强，亚像素全连接层由全连接层和元素排列构成，根据公式(11)得到全连接层输出r2(r＝2)通道与输入数据维数相同的数据，
[0065]
x
sr
＝f4(x
lr
)＝ps(w3*f2(x
lr
))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(11)
[0066]
其中，x
sr
是espfcn网络生成的高分辨率样本，ps算子能够将张量的形状由h
×
w
×
c
·
r2重新排列成rh
×
rw
×
c，ps算子的数学描述如式(12)所示：
[0067]
ps(t)
p,q
＝t
|p/r|
·
|q/r|
·
r
·
mod(q/r)+mod(p/r)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(12)
[0068]
其实质是对四通道的低分辨率特征进行周期性的排列，最终得到一组高分辨率特征；
[0069]
步骤3，使用均方误差(mse)度量真实低分辨率样本与生成的低分辨率特征的差异程度，其计算公式如下：
[0070][0071]
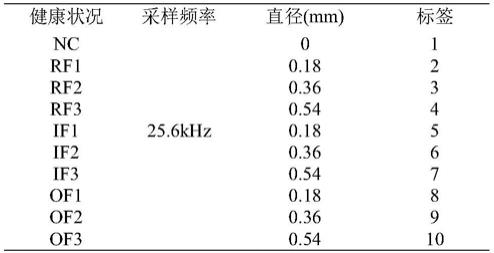
为了验证espfcn对样本分辨率增强的效果，我们设计了一个模拟轴承失效的实验平台，如图5所示。该平台主要由电动机、联轴器、轴承座、齿轮箱和制动器组成。轴承底座的振动信号由带振动传感器的lms数据采集仪采集，传感器置于轴承座侧。采样频率为25.6khz。发动机转速3000r/min，图6所示的三种轴承类型均为n205eu圆柱滚子轴承。如表1所示，轴承类型有四种健康状态:正常状态(nc)、内圈故障(if)、外圈故障(of)和滚珠故障(rf)。每种故障类型有三种不同程度的损害:0.18mm、0.36mm和0.54mm。轴承健康状况分为十种，每种状态包含200个样本。
[0072]
表1
[0073]
[0074]
原始输入样本中包含的点数通过式(13)计算得到：
[0075][0076]
可以看出，在采样频率为25.6khz，电机转速为3000r/min的情况下，电机每转一圈采样设备将采集512个数据点。因此，将每600个数据点设为一个低分辨率的样本，每个样本经过傅里叶变换后得到300个傅里叶系数。设置2400个数据点为一个高分辨率样本，每个样本经过傅里叶变换后得到1200个傅里叶系数。此外,所有实验样本数据在相同负载下采集espfcn的参数设置如下：迭代次数为40次，学习率为10-3
，激活函数为relu。使用sae测试espfcn生成数据的有效性。使用低分辨率样本作为espfcn的输入样本，并将生成的数据集作为sae的训练样本，将原始的高分辨率数据集作为测试样本。另外两种方法从不同故障类型的样本中随机抽取50％作为训练集，剩余50％作为测试集。
[0077]
图5显示了三种数据类型的频域图(低分辨率频谱图、espfcn生成的频谱图和高分辨率的频谱图)。可以看出，从频谱图中很难直观的区分不同的故障类型，因此有必要使用基于深度学习的分类网络来提取样本特征，以更好的区分故障类型。当采样设备的采样频率越高，采集的数据点越多，数据包含的特征越多，判别网络的训练效果越好。由于低分辨率样本只含有一圈的轴承数据，所以特征较少。生成的高分辨率样本的分布规律符合高分辨率样本的分布规律，特征较为相似。但由于低分辨率样本的局限性，生成数的高分辨率样本和高分辨率样本存在一定的差异性。
[0078]
为了验证该方法的有效性，将espfcn生成的数据集和两个比较数据(低维数据集和高维数据集)分别作为sae的输入数据集。实验结果如图6所示，同时采用表2展示了实验结果的具体数据。实验重复15次以减少随机性的影响。可以看出，低分辨率数据集的结果并不理想，平均准确率为95.78％，这是因为低分辨率样本包含的特征相对较少，从而导致判别网络欠拟合；espfcn的平均准确率为98.25％,这是因为espfcn使低分辨率的数据增强为原来的四倍,增强后的样本包含更多的特征信息，从而能够更好的训练判别网络；高分辨率数据的平均准确率最高，达到了99.94％。不同运行状况下的其他样本被很好地分离。
[0079]
利用皮尔逊相关系数pcc评估生成样本与原始高分辨率样本之间的相似性，pcc的值越大，表示两者之间的相关性越强，pcc的计算公式如(15)所示：
[0080][0081]
其中，x表示espfcn生成的样本，y表示原始高分辨率样本，cov(
·
,
·
)是协方差，σ
x
和σ
y
分别是x和y的标准差，μ
x
和μ
y
分别是x和y的均值，e是期望，espfcn与原始高分辨率样本的pcc为0.81，说明这两类样本之间的相似性较强。
[0082]
表2
[0083]
[0084][0085]
为了直观地展示这三种数据集的分类效果，我们采用t-sne(t-distributed random neighbor)方法将sae隐含层特征映射到三维特征中。从图7(a)可以看出，低分辨率数据的聚类效果并不理想，部分样本相互混合，不同样本之间存在不同程度的误分类；在图7(b)所示,espfcn的聚类效果优于低分辨率样本的聚类效果,除了少数of3和if1样本发生了误分类的情况,其他不同的健康状况的样本很好分离,分类结果接近图7(c)高分辨率样本的分类结果。
[0086]
此外，为了了解espfcn如何提高样本的分辨率，我们研究了该方法的特征学习过程。，在同一全连接层中，不同通道的特征是不同的,除了少数通道的特征区分度较大，其余通道的特征较为相似。随着全连接层数的增加，隐层的通道数从64通道减少到4通道，通道数量的缩减导致不同通道之间特征的分化程度更加明显，增大了特征的多样性。由于espfcn能够同时增强十种健康状况的低分辨率样本，因此图11随机展示了样本为正常工况(nc)时的三种数据类型的频谱图。由图8(a)可知，低分辨率样本的样本点只有300，因此其特征明显少于其他两种数据类型的特征。由图8(b)所示，相比于低分辨率样本，espfcn生成的高分辨率样本含有更多的数据点，特征也更加的明显，而且其频谱与图8(c)的高分辨率频谱具有一致的特征趋势，即由espfcn生成的高分辨率样本在一定程度上还原了真实的高分辨率样本的频谱。
[0087]
为了提高低分辨率样本的分辨率，提出了一种有效的深度学习框架
--
espfcn。低分辨率样本经全连接层输出四通道特征，然后通过亚像素全连接层将四通道的特征合成高分辨率特征，实现样本由低分辨率到高分辨率的转变，样本的特征进而增多，有利于对机械的健康状况进行准确的分析和诊断。在轴承实验的基础上，提出了一种测试策略来评估espfcn的可行性。生成的数据集和原始数据集分别作为sae分类器模型的训练集和测试集。分类结果表明，本文所提出的espfcn模型在恒转速下的数据扩充是可行的，可以产生可靠的仿真样本。本文试图为机械故障诊断任务建立一个预测框架，生成数据的分析验证和提出框架的隐层可视化展示，有利于后续的故障诊断。
[0088]
当然，上述说明并非是对本发明的限制，本发明也并不仅限于上述举例，本技术领域的技术人员在本发明的实质范围内所做出的变化、改型、添加或替换，也应属于本发明的保护范围。