页岩油储层渗透率的预测方法及装置与流程
1.本发明涉及油储层勘测技术领域,尤其涉及页岩油储层渗透率的预测方法及装置。
背景技术:
2.本部分旨在为权利要求书中陈述的本发明实施例提供背景或上下文。此处的描述不因为包括在本部分中就承认是现有技术。
3.随着常规油气资源发现的难度逐年增大,非常规油气在油气勘探领域的比重越来越大。高丰度、大面积分布的页岩油气资源成为非常规领域热点目标,尤其在美国巴肯等大型盆地页岩油的成功开发,极大地提升了页岩油的战略地位,促进了我国油气勘探工作者加强国内各大含油气盆地页岩油的勘探和研究。虽然我国在页岩油领域的起步较晚,但通过多年的攻关研究,近年在我国四川、松辽、鄂尔多斯、准噶尔、柴达木等盆地页岩油勘探取得较大地突破,相继发现了储量可观的页岩油资源。
4.而渗透率是刻画页岩油储集层特征和地下流体流动性的重要参数,对开发方案设计、地下流体特征研究均具有重要作用,因此对地下油储集层的渗透率参数进行预测具有重要意义。目前,石油工业界储集层渗透率预测仍主要以测井数据和岩心分析为主,主要方法包括压汞实验分析、核磁共振分析等,但是这些实验手段相对昂贵且观测数据所覆盖储集层范围有限,难以实现对储集层渗透率大尺度横向分布规律的研究。
5.因此,以地震数据进行储集层渗透率预测成为热门趋势。地震数据可提供丰富的地层横向展布信息,若可利用地震数据进行储集层渗透率预测,可为储集层预测提供有效的渗流场信息,对储集层评价和油气藏开发具有重要意义。但,利用地震数据进行储集层渗透率预测一直是储集层预测的前沿和难点问题,众多学者对此进行了诸多研究,主要技术方法有经验法、地震属性分析法和地质统计学模拟法等。经验法即通过井中实测孔隙度和渗透率散点交汇图进行拟合,将拟合公式应用于实际地震数据中。在岩石孔隙较为复杂时,往往很难得到孔隙度与渗透率的线性回归关系,导致该二元线性回归方法存在较大误差。地震属性分析法即采用神经网络等方法将地震属性与渗透率建立非线性神经网络关系,然后将空间分布的地震属性体转换为渗透率体,该技术可能存在因渗透率样本较少导致神经网络过拟合现象。地质统计学模拟方法即采用协克里金插值方法,以井点渗透率为主变量,通过次变量地震属性趋势约束对渗透率曲线进行插值,该方法要求井资料丰富,而且要求井在平面上分布较均匀。
6.由于页岩油储层的岩石孔隙较为复杂,使得在页岩油储层空间分布上渗透率与孔隙度并非总是一一对应。因此在使用上述技术方法对页岩油储层渗透率进行预测时,会使预测结果存在较大误差,造成页岩油储层渗透率预测精度较低的问题;同时,还会造成页岩油储层渗透率预测结果产生多解性的问题。
技术实现要素:
7.本发明实施例提供一种页岩油储层渗透率的预测方法,用以提高渗透率预测精度,降低预测结果多解性,该方法包括:
8.根据页岩油储层的取心资料,计算页岩油储层的井位处流动单元指数;
9.根据页岩油储层的井位处流动单元指数,对页岩油储层的流动单元进行分类;
10.根据流动单元的分类结果,通过多元回归分析建立页岩油储层流动单元的渗透率计算模型;所述渗透率计算模型用于表征页岩油储层的井位处有效孔隙度与渗透率之间的关联关系;
11.根据页岩油储层的地震数据,预测页岩油储层的井位处有效孔隙度,以及反演页岩油储层的流动单元指数数据体;
12.根据页岩油储层流动单元的渗透率计算模型,页岩油储层的井位处有效孔隙度和流动单元指数数据体,预测页岩油储层的渗透率。
13.本发明实施例还提供一种页岩油储层渗透率的预测装置,用以提高渗透率预测精度,降低预测结果多解性,该装置包括:
14.计算模块,用于根据页岩油储层的取心资料,计算页岩油储层的井位处流动单元指数;
15.分类模块,用于根据页岩油储层的井位处流动单元指数,对页岩油储层的流动单元进行分类;
16.建模模块,用于根据流动单元的分类结果,通过多元回归分析建立页岩油储层流动单元的渗透率计算模型;所述渗透率计算模型用于表征页岩油储层的井位处有效孔隙度与渗透率之间的关联关系;
17.预测模块,用于根据页岩油储层的地震数据,预测页岩油储层的井位处有效孔隙度,以及反演页岩油储层的流动单元指数数据体;
18.渗透率预测模块,用于根据页岩油储层流动单元的渗透率计算模型,页岩油储层的井位处有效孔隙度和流动单元指数数据体,预测页岩油储层的渗透率。
19.本发明实施例还提供一种计算机设备,包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序,所述处理器执行所述计算机程序时实现上述页岩油储层渗透率的预测方法。
20.本发明实施例还提供一种计算机可读存储介质,所述计算机可读存储介质存储有执行上述页岩油储层渗透率的预测方法的计算机程序。
21.本发明实施例中,根据页岩油储层的取心资料,计算页岩油储层的井位处流动单元指数;根据页岩油储层的井位处流动单元指数,对页岩油储层的流动单元进行分类;根据流动单元的分类结果,通过多元回归分析;所述渗透率计算模型用于表征页岩油储层的井位处有效孔隙度与渗透率之间的关联关系;根据页岩油储层的地震数据,预测页岩油储层的井位处有效孔隙度,以及反演页岩油储层的流动单元指数数据体;根据页岩油储层流动单元的渗透率计算模型,页岩油储层的井位处有效孔隙度和流动单元指数数据体,预测页岩油储层的渗透率,与现有技术对比,通过对页岩油储层流动单元进行分类,通过多元回归分析建立页岩油储层流动单元的渗透率计算模型,解决了储层空间分布对渗透率预测精度产生影响的问题,同时通过建立渗透率计算模型,提高了页岩油储层渗透率的预测精度,同
时,降低了预测结果的多解性。
附图说明
22.为了更清楚地说明本发明实施例或现有技术中的技术方案,下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍,显而易见地,下面描述中的附图仅仅是本发明的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动的前提下,还可以根据这些附图获得其他的附图。在附图中:
23.图1为本发明实施例中一种页岩油储层渗透率的预测方法的流程示意图;
24.图2为本发明实施例中一种页岩油储层渗透率的预测方法的具体示例图;
25.图3为本发明实施例中一种页岩油储层渗透率的预测方法的具体示例图;
26.图4为本发明实施例中一种页岩油储层渗透率的预测方法的具体示例图;
27.图5为本发明实施例中一种页岩油储层渗透率的预测方法的具体示例图;
28.图6为本发明实施例中一种页岩油储层渗透率的预测装置的结构示意图。
具体实施方式
29.为使本发明实施例的目的、技术方案和优点更加清楚明白,下面结合附图对本发明实施例做进一步详细说明。在此,本发明的示意性实施例及其说明用于解释本发明,但并不作为对本发明的限定。
30.图1为本发明实施例中一种页岩油储层渗透率的预测方法的流程示意图,如图1所示,本发明实施例提供的页岩油储层渗透率的预测方法,可以包括:
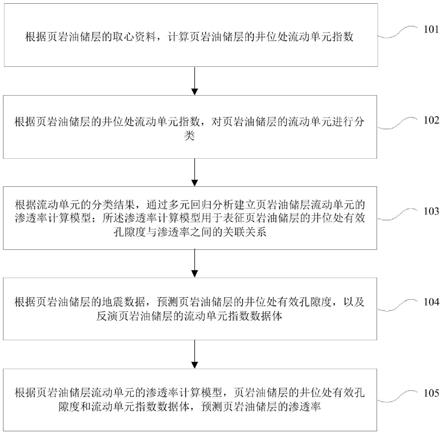
31.步骤101:根据页岩油储层的取心资料,计算页岩油储层的井位处流动单元指数;
32.步骤102:根据页岩油储层的井位处流动单元指数,对页岩油储层的流动单元进行分类;
33.步骤103:根据流动单元的分类结果,通过多元回归分析建立页岩油储层流动单元的渗透率计算模型;所述渗透率计算模型用于表征页岩油储层的井位处有效孔隙度与渗透率之间的关联关系;
34.步骤104:根据页岩油储层的地震数据,预测页岩油储层的井位处有效孔隙度,以及反演页岩油储层的流动单元指数数据体;
35.步骤105:根据页岩油储层流动单元的渗透率计算模型,页岩油储层的井位处有效孔隙度和流动单元指数数据体,预测页岩油储层的渗透率。
36.本发明实施例中,根据页岩油储层的取心资料,计算页岩油储层的井位处流动单元指数;根据页岩油储层的井位处流动单元指数,对页岩油储层的流动单元进行分类;根据流动单元的分类结果,通过多元回归分析;所述渗透率计算模型用于表征页岩油储层的井位处有效孔隙度与渗透率之间的关联关系;根据页岩油储层的地震数据,预测页岩油储层的井位处有效孔隙度,以及反演页岩油储层的流动单元指数数据体;根据页岩油储层流动单元的渗透率计算模型,页岩油储层的井位处有效孔隙度和流动单元指数数据体,预测页岩油储层的渗透率,与现有技术对比,通过对页岩油储层流动单元进行分类,通过多元回归分析建立页岩油储层流动单元的渗透率计算模型,解决了储层空间分布对渗透率预测精度产生影响的问题,同时通过建立渗透率计算模型,提高了页岩油储层渗透率的预测精度,同
时,降低了预测结果的多解性。
37.具体实施时,首先根据页岩油储层的取心资料,计算页岩油储层的井位处流动单元指数。
38.实施例中,按如下公式根据页岩油储层的取心资料,计算页岩油储层的井位处流动单元指数:
[0039][0040]
其中,fziw为页岩油储层的井位处流动单元指数,单位为μm;fs为孔隙形状因子,无量纲;τ为弯曲度,无量纲;s
gv
为颗粒比表面积,单位为μm-1
。
[0041]
在上述实施例中,可利用研究区页岩油储层的取心资料,根据上述公式计算储层的流动单元指数(fzi,flowzone indicator)。fzi与岩石的孔隙结构特征密切相关,如果fzi值接近,则岩石的孔隙结构特征相似,使得孔隙度与渗透率之间表现出良好的相关性。因此,根据fzi的大小划分出流动单元之后,即可利用孔隙度对渗透率进行准确的分类评价。
[0042]
结合实际工区已钻井的测井资料和岩石物理实验数据,可以建立fzi指数与孔隙结构参数之间的拟合关系。
[0043]
实施例中,可根据如下步骤确定计算页岩油储层的井位处流动单元指数的公式:
[0044]
1、结合poisseuille定律与darcy定律,并假设多孔介质由许多直的毛细管组成,kozeny提出了渗透率k、有效孔隙度与毛细管半径三者之间的关系公式,即:
[0045][0046]
其中,k表示渗透率,r表示毛细管半径;φ表示有效孔隙度;
[0047]
2、引入弯曲度、形状因子与颗粒比表面积参数,改进了kozeny公式,提出了广义的kozeny-carman公式,即:
[0048][0049]
3、将kozeny-carman公式等号两边同时除以孔隙度并开方,再把渗透率单位由d转化为md,得到式(3):
[0050][0051]
其中,fziw为页岩油储层的井位处流动单元指数,单位为μm;fs为孔隙形状因子,无量纲;τ为弯曲度,无量纲;s
gv
为颗粒比表面积,单位为μm-1
。
[0052]
发明人发现页岩油储层的渗透率还受到孔隙结构的影响。不同孔隙结构的岩石,孔隙度与渗透率对应关系存在明显差异,只有结合储集层孔隙结构进行渗透率预测才能降低多解性,提高预测精度。经检索,目前没有针对页岩油储层利用地震资料预测储层渗透率的空间分布的相关技术。本发明实施例通过根据页岩油储层的取心资料,计算页岩油储层的标准孔隙度和储层品质指数,降低了孔隙结构对预测页岩油储层的渗透率的影响。
[0053]
具体实施时,在根据页岩油储层的取心资料,计算页岩油储层的井位处流动单元
指数后,根据页岩油储层的井位处流动单元指数,对页岩油储层的流动单元进行分类;根据流动单元的分类结果,通过多元回归分析建立页岩油储层流动单元的渗透率计算模型;所述渗透率计算模型用于表征页岩油储层的井位处有效孔隙度与渗透率之间的关联关系。
[0054]
实施例中,本发明实施例提供的页岩油储层渗透率的预测方法,还可以包括:根据页岩油储层的取心资料,计算页岩油储层的标准孔隙度和储层品质指数;根据页岩油储层的井位处流动单元指数,对页岩油储层的流动单元进行分类,可以包括:根据页岩油储层的井位处流动单元指数,标准孔隙度和储层品质指数,应用数理统计法对页岩油储层的流动单元进行分类;根据流动单元的分类结果,通过多元回归分析建立页岩油储层流动单元的渗透率计算模型,可以包括:根据流动单元的分类结果,结合页岩油储层的标准孔隙度和储层品质指数,通过多元回归分析建立页岩油储层流动单元的渗透率计算模型。
[0055]
在上述实施例中,可通过应用数理统计法对页岩油储层的流动单元进行分类,根据流动单元分类的结果,可将页岩油储层的流动单元按照物性的好坏划分成多个种类。
[0056]
举一实例,如图2所示,图2中展示了根据页岩油储层的井位处流动单元指数,对页岩油储层的流动单元进行分类的结果。
[0057]
发明人在对研究区内岩石物理实验标准柱塞样的孔隙度与渗透率交会图进行研究后发现,页岩油储层孔隙度与渗透率相关性差,单一的孔隙度与渗透率回归模型已经难以准确计算渗透率的问题。本发明实施例可解决上述问题。
[0058]
具体实施时,可按如下公式计算页岩油储层的标准孔隙度:
[0059][0060]
其中,φz为页岩油储层的标准孔隙度,无量纲;φ为井位处有效孔隙度,无量纲。
[0061]
按如下公式计算页岩油储层的储层品质指数:
[0062][0063]
其中,rqi为页岩油储层的储层品质指数,单位为μm;k为页岩油储层的井位处渗透率,单位为md;φz为页岩油储层的标准孔隙度,无量纲。
[0064]
在上述实施例中,根据页岩油储层的井位处流动单元指数,标准孔隙度和储层品质指数,应用数理统计法可实现对页岩油储层的流动单元进行分类的目的,有助于提升页岩油储层的流动单元分类的准确性。
[0065]
进一步地,在对页岩油储层的标准孔隙度和储层品质指数进行计算后,可将页岩油储层的标准孔隙度和储层品质指数进行组合分析,根据图中标准孔隙度和储层品质指数的交会关系,结合fzi,可以将页岩油储层的流动单元进行分类。
[0066]
举一例,如图3所示,图3展示了将页岩油储层的标准孔隙度和储层品质指数进行组合分析的效果图。
[0067]
具体实施时,可按如下公式建立页岩油储层流动单元的渗透率计算模型:
[0068][0069]
其中,perm为页岩油储层的渗透率,单位为md;φ为井位处有效孔隙度,无量纲;fzi为页岩油储层的流动单元指数,单位为μm。
[0070]
在上述实施例中,通过建立页岩油储层流动单元的渗透率计算模型,建立了不同工区页岩油储层的井位处有效孔隙度与页岩油储层的渗透率之间的关联关系,有助于在后续步骤中预测页岩油储层的渗透率。
[0071]
举一例,如图4所示,图4展示了不同fzi分类条件下,井位处有效孔隙度与渗透率的交会图。将页岩油储层的流动单元划分出5类流动单元,且5类流动单元的趋势线相互平行,斜率都为1;再根据储层的划分结果,经回归分析,建立这5类流动单元的渗透率计算模型。
[0072]
具体实施时,在根据流动单元的分类结果,通过多元回归分析建立页岩油储层流动单元的渗透率计算模型后,根据页岩油储层的地震数据,预测页岩油储层的井位处有效孔隙度,以及反演页岩油储层的流动单元指数数据体。
[0073]
实施例中,根据页岩油储层的地震数据,预测页岩油储层的井位处有效孔隙度,可以包括:根据页岩油储层的地震数据,计算页岩油储层的纵波速度,横波速度和密度;通过叠前弹性参数反演,根据页岩油储层的纵波速度,横波速度和密度,预测页岩油储层的井位处有效孔隙度。
[0074]
在上述实施例中,可利用页岩油储层的叠前地震数据的反演结果,计算出地震纵波和横波的速度和密度,再利用叠前反演结果开展页岩油储层的井位处有效孔隙度预测,可实际计算出任一工区页岩油储层的井位处有效孔隙度。
[0075]
具体实施时,本发明实施例提供的页岩油储层渗透率的预测方法,还可以包括:对取心资料进行多元统计分析,得到流动单元指数与测井曲线的拟合关系;根据流动单元指数与测井曲线的拟合关系,计算页岩油储层的流动单元指数曲线;根据页岩油储层的地震数据,反演页岩油储层的流动单元指数数据体,可以包括:结合页岩油储层的流动单元指数曲线,对页岩油储层的地震数据进行多属性反演,得到页岩油储层的流动单元指数数据体。
[0076]
实施例中,流动单元指数数据体(fzi数据体)的反演时可使用页岩油储层的流动单元指数曲线,并结合“相控随机模拟”思想,参照样本空间分布距离和曲线分布特征建立初始模型,代替变差函数分析空间变异结构,对高频成分进行无偏最优估计而得出。在贝叶斯框架下联合似然函数分布和先验分布得到后验概率密度分布,并将其作为目标函数。不断扰动模型参数,使后验概率密度函数值最大时的解作为可行随机实现,取多次可行实现的均值作为期望值输出,即可反演得到fzi数据体。
[0077]
在上述实施例中,发明人经分析发现fzi与岩石的孔隙结构特征密切相关。如果fzi接近,则岩石的孔隙结构特征相似,使得孔隙度与渗透率之间表现出良好的相关性。因此,根据fzi的大小划分出流动单元之后,即可利用孔隙度对渗透率进行准确的分类评价。
页岩油储层中储层孔隙结构复杂主要由黏土矿物含量及有机质演化程度决定,而在常规测井曲线中,自然伽马(gr)、中子(cnl)和密度(den)曲线对黏土矿物含量及有机质演化程度有一定的响应,为此首先在取心资料中通过多元统计分析得到fzi与常规测井曲线的拟合关系。然后利用这个关系在页岩油储层段计算得到一条fzi曲线。
[0078]
具体实施时,在根据页岩油储层的地震数据,预测页岩油储层的井位处有效孔隙度,以及反演页岩油储层的流动单元指数数据体后,根据页岩油储层流动单元的渗透率计算模型,页岩油储层的井位处有效孔隙度和流动单元指数数据体,预测页岩油储层的渗透率。
[0079]
实施例中,在fzi数据体预测的基础上,按照fzi分类标准对研究区fzi指数体中不同类型的地区,根据井位处有效孔隙度与渗透率之间的关系,利用页岩油储层流动单元的渗透率计算模型,即可将井位处有效孔隙度的预测结果转换为研究区的渗透率结果,最终预测出页岩油储层的渗透率。
[0080]
举一例,如图5所示,图5对利用常规方法与本发明实施例提供方法(即fzi曲线分类后渗透率反演方法)得到的渗透率剖面进行了对比,图5中利用本发明实施例中页岩油储层渗透率的预测方法计算的得到的渗透率剖面图的纵向分辨率明显要高于现有技术下常规方法的渗透率计算结果。图5中,南充2井所在位置渗透率较好的层段厚度为10m,而常规方法计算的渗透率较好的层段厚约15m,经本发明实施例提供的方法计算的层段厚度为11m,在误差容许范围内。另外在西充2和南充2之间,常规方法计算的得到的渗透率较好的厚度也要大于经本发明实施例例提供的方法计算的渗透率计算结果。
[0081]
本发明实施例中,根据页岩油储层的取心资料,计算页岩油储层的井位处流动单元指数;根据页岩油储层的井位处流动单元指数,对页岩油储层的流动单元进行分类;根据流动单元的分类结果,通过多元回归分析;所述渗透率计算模型用于表征页岩油储层的井位处有效孔隙度与渗透率之间的关联关系;根据页岩油储层的地震数据,预测页岩油储层的井位处有效孔隙度,以及反演页岩油储层的流动单元指数数据体;根据页岩油储层流动单元的渗透率计算模型,页岩油储层的井位处有效孔隙度和流动单元指数数据体,预测页岩油储层的渗透率,与现有技术对比,通过对页岩油储层流动单元进行分类,通过多元回归分析建立页岩油储层流动单元的渗透率计算模型,解决了储层空间分布对渗透率预测精度产生影响的问题,同时通过建立渗透率计算模型,提高了页岩油储层渗透率的预测精度,同时,降低了预测结果的多解性。
[0082]
如上所述,为了提高页岩油储层渗透率预测的精度,降低利用地震资料预测页岩油储层渗透率的多解性,提高纵向渗透率预测的分辨率,本发明实施例采用储集的标准孔隙度、弹性参数及流动单元指数进行页岩油储层的分类,在每类流动单元中采用孔隙度、纵横波速度及流动单元指数进行多元回归得到预测渗透率,实际应用验证了该方法的有效性,为页岩油储层的渗透性参数空间分布预测提供了可行思路。举一实例,如在四川盆地川中某地区开展的某实验,从实际的预测结果来看,本发明实施例预测的页岩油储层的渗透率的效果较现有技术要更优越,通过与实际测试资料的对比,本发明实施例的预测结果在纵向上的分辨率更高,精度更高。
[0083]
本发明实施例中还提供了一种页岩油储层渗透率的预测装置,如下面的实施例所述。由于该装置解决问题的原理与页岩油储层渗透率的预测方法相似,因此该装置的实施
可以参见页岩油储层渗透率的预测方法的实施,重复之处不再赘述。
[0084]
图6为本发明实施例中一种页岩油储层渗透率的预测装置的结构示意图,如图6所示,本发明实施例提供的一种页岩油储层渗透率的预测装置,可以包括:
[0085]
计算模块01,用于根据页岩油储层的取心资料,计算页岩油储层的井位处流动单元指数;
[0086]
分类模块02,用于根据页岩油储层的井位处流动单元指数,对页岩油储层的流动单元进行分类;
[0087]
建模模块03,用于根据流动单元的分类结果,通过多元回归分析建立页岩油储层流动单元的渗透率计算模型;所述渗透率计算模型用于表征页岩油储层的井位处有效孔隙度与渗透率之间的关联关系;
[0088]
预测模块04,用于根据页岩油储层的地震数据,预测页岩油储层的井位处有效孔隙度,以及反演页岩油储层的流动单元指数数据体;
[0089]
渗透率预测模块05,用于根据页岩油储层流动单元的渗透率计算模型,页岩油储层的井位处有效孔隙度和流动单元指数数据体,预测页岩油储层的渗透率。
[0090]
在一个实施例中,计算模块,具体用于:按如下公式根据页岩油储层的取心资料,计算页岩油储层的井位处流动单元指数:
[0091][0092]
其中,fziw为页岩油储层的井位处流动单元指数,单位为μm;fs为孔隙形状因子,无量纲;τ为弯曲度,无量纲;s
gv
为颗粒比表面积,单位为μm-1
。
[0093]
在一个实施例中,还包括:页岩油储层参数计算模块,用于:根据页岩油储层的取心资料,计算页岩油储层的标准孔隙度和储层品质指数;
[0094]
分类模块,具体用于:根据页岩油储层的井位处流动单元指数,标准孔隙度和储层品质指数,应用数理统计法对页岩油储层的流动单元进行分类;
[0095]
建模模块,具体用于:根据流动单元的分类结果,结合页岩油储层的标准孔隙度和储层品质指数,通过多元回归分析建立页岩油储层流动单元的渗透率计算模型。
[0096]
在一个实施例中,页岩油储层参数计算模块,具体用于:按如下公式计算页岩油储层的标准孔隙度:
[0097][0098]
其中,φz为页岩油储层的标准孔隙度,无量纲;φ为井位处有效孔隙度,无量纲。在一个实施例中,页岩油储层参数计算模块,具体用于:按如下公式计算页岩油储层的储层品质指数:
[0099][0100]
其中,rqi为页岩油储层的储层品质指数,单位为μm;k为页岩油储层的井位处渗透率,单位为md;φz为页岩油储层的标准孔隙度,无量纲。
[0101]
在一个实施例中,建模模块,具体用于:按如下公式建立页岩油储层流动单元的渗
透率计算模型:
[0102][0103]
其中,perm为页岩油储层的渗透率,单位为md;φ为井位处有效孔隙度,无量纲;fzi为页岩油储层的流动单元指数,单位为μm。
[0104]
在一个实施例中,预测模块,具体用于:
[0105]
根据页岩油储层的地震数据,计算页岩油储层的纵波速度,横波速度和密度;
[0106]
通过叠前弹性参数反演,根据页岩油储层的纵波速度,横波速度和密度,预测页岩油储层的井位处有效孔隙度。
[0107]
在一个实施例中,还包括:拟合关系确定模块,用于:对取心资料进行多元统计分析,得到流动单元指数与测井曲线的拟合关系;
[0108]
根据流动单元指数与测井曲线的拟合关系,计算页岩油储层的流动单元指数曲线;
[0109]
预测模块,具体用于:结合页岩油储层的流动单元指数曲线,对页岩油储层的地震数据进行多属性反演,得到页岩油储层的流动单元指数数据体。
[0110]
本发明实施例还提供一种计算机设备,包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序,所述处理器执行所述计算机程序时实现上述页岩油储层渗透率的预测方法。
[0111]
本发明实施例还提供一种计算机可读存储介质,所述计算机可读存储介质存储有执行上述页岩油储层渗透率的预测方法的计算机程序。
[0112]
本发明实施例中,根据页岩油储层的取心资料,计算页岩油储层的井位处流动单元指数;根据页岩油储层的井位处流动单元指数,对页岩油储层的流动单元进行分类;根据流动单元的分类结果,通过多元回归分析;所述渗透率计算模型用于表征页岩油储层的井位处有效孔隙度与渗透率之间的关联关系;根据页岩油储层的地震数据,预测页岩油储层的井位处有效孔隙度,以及反演页岩油储层的流动单元指数数据体;根据页岩油储层流动单元的渗透率计算模型,页岩油储层的井位处有效孔隙度和流动单元指数数据体,预测页岩油储层的渗透率,与现有技术对比,通过对页岩油储层流动单元进行分类,通过多元回归分析建立页岩油储层流动单元的渗透率计算模型,解决了储层空间分布对渗透率预测精度产生影响的问题,同时通过建立渗透率计算模型,提高了页岩油储层渗透率的预测精度,同时,降低了预测结果的多解性。
[0113]
本领域内的技术人员应明白,本发明的实施例可提供为方法、系统、或计算机程序产品。因此,本发明可采用完全硬件实施例、完全软件实施例、或结合软件和硬件方面的实施例的形式。而且,本发明可采用在一个或多个其中包含有计算机可用程序代码的计算机可用存储介质(包括但不限于磁盘存储器、cd-rom、光学存储器等)上实施的计算机程序产品的形式。
[0114]
本发明是参照根据本发明实施例的方法、设备(系统)、和计算机程序产品的流程图和/或方框图来描述的。应理解可由计算机程序指令实现流程图和/或方框图中的每一流程和/或方框、以及流程图和/或方框图中的流程和/或方框的结合。可提供这些计算机程序指令到通用计算机、专用计算机、嵌入式处理机或其他可编程数据处理设备的处理器以产生一个机器,使得通过计算机或其他可编程数据处理设备的处理器执行的指令产生用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的装置。
[0115]
这些计算机程序指令也可存储在能引导计算机或其他可编程数据处理设备以特定方式工作的计算机可读存储器中,使得存储在该计算机可读存储器中的指令产生包括指令装置的制造品,该指令装置实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能。
[0116]
这些计算机程序指令也可装载到计算机或其他可编程数据处理设备上,使得在计算机或其他可编程设备上执行一系列操作步骤以产生计算机实现的处理,从而在计算机或其他可编程设备上执行的指令提供用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的步骤。
[0117]
以上所述的具体实施例,对本发明的目的、技术方案和有益效果进行了进一步详细说明,所应理解的是,以上所述仅为本发明的具体实施例而已,并不用于限定本发明的保护范围,凡在本发明的精神和原则之内,所做的任何修改、等同替换、改进等,均应包含在本发明的保护范围之内。
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1