一种基于解析四维集合变分的提高海洋预报精度的方法

1.本发明涉及一种提高海洋预报精度的方法。特别是涉及一种基于解析四维集合变分的提高海洋预报精度的方法。


背景技术：

2.数据同化算法作为数据同化系统的重要组成部分在过去的几十年间取得了极大的研究进展，然而，在高维空间、多尺度、非线性、非高斯、复杂不确定性以及状态量空间相关性等多种因素的综合作用下，现有的数据同化算法的不足日益突出。
3.要得到一个准确的预报结果必须满足两个条件：一是数值预报模式能足够准确地模拟海洋系统的演变过程，即控制海水运动的物理规律有较好地描述；二是模拟初值能足够精确地反映初始时刻的状态。所以好的初始场越来越被认为是整个数值预报领域的一个重要方面，初始场的精确性直接影响着海洋数值预报的成败。变分同化的作用就在于：通过一次循环，可以提高一点初始场的优化程度，以减小模式输出值与模式“真值”及观测值的差距。模式对初值高度敏感，如果初猜值的误差大到一定程度，则会导致目标函数下降很慢，经过多次循环迭代后都难以达到收敛，造成同化失败。
4.背景误差协方差矩阵的精确定义是构建高水平数据同化系统的先决条件。传统四维变分方法通常是从物理、统计和计算效率等方面考虑构造简化和近似的背景误差协方差模型，忽略了背景误差协方差的非均匀、各向异性和时变等特性，效果不理想。此外，传统四维变分方法需要通过编写伴随模式求取目标函数的梯度，要保证相应的伴随模式严格成立，通常的作法是先根据切线性模式程序一一对应地写出伴随程序，工作量巨大。四维集合变分方法利用集合同化的样本实时估计背景误差方差，能够精确估计流依赖背景误差协方差，而且四维集合变分方法不需要编写伴随模式。但是现有的四维集合变分方法应用于非线性较强的系统时效果会不如传统四维变分方法。


技术实现要素：

5.本发明所要解决的技术问题是，针对存在的问题，提供一种可以在在非线性较强的情况下较好地进行初始场优化的基于解析四维集合变分的提高海洋预报精度的方法。
6.本发明所采用的技术方案是：一种基于解析四维集合变分的提高海洋预报精度的方法，包括如下步骤：
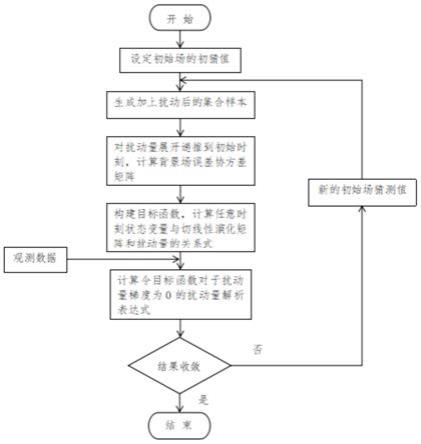
7.1)将初始场猜测值和外界强迫场分别加上扰动值形成集合样本，根据所述的集合样本改写解析四维集合变分的演化方程，并展开扰动量直至递推到初始时刻；
8.2)当初始场猜测值与外界强迫场统计无关时，得到两个分别包含切线性演化矩阵和对应的伴随矩阵信息的特殊的背景场误差协方差矩阵；
9.3)在传统四维集合变分的基础上，对初始场猜测值附近进行扰动展开，得到未来任意时刻状态变量与切线性演化矩阵和扰动量的关系，并构建扰动后的目标函数；
10.4)求出扰动后的目标函数对于扰动量的梯度；
11.5)在相空间按扰动量解析解的方向以设定步长进行线性搜索，更新初始场猜测值，返回步骤1)，直至扰动后的目标函数对于扰动量的梯度无限趋近于零，得到的初始场猜测值为最优的初始场猜测值。
12.本发明的一种基于解析四维集合变分的提高海洋预报精度的方法，通过直接求取模式初始场的最优扰动量解析解进行初始场优化，保留了已有四维集合变分方法背景误差协方差矩阵更加精确且不需要编写伴随模式的优点，同时解决了已有四维集合变分方法不能应用于非线性较强的海域的问题，可以在在非线性较强的情况下较好地进行初始场优化。本发明的方法与传统四维变分方法相比，最优增量的解析解中不再包含切线性演化矩阵和伴随矩阵，大大增强了算法的可移植性，可以应用在非线性较强的情况上，极大提高了四维集合变分方法的适用性，有效减小了预报误差，具有较大的研究意义和广泛的应用前景。
附图说明
13.图1是本发明一种基于解析四维集合变分的提高海洋预报精度的方法的流程图；
14.图2是对lorenz-63模型进行初始场优化后的真值、背景值和数据同化结果解的对比图；
15.图3是使用优化初始场a-4denvar和4dvar两种方案数据同化的平均均方根误差对比图；
16.图4是迭代函数的三个变量的均方根误差。
具体实施方式
17.下面结合实施例和附图对本发明的一种基于解析四维集合变分的提高海洋预报精度的方法做出详细说明。
18.如图1所示，本发明的一种基于解析四维集合变分的提高海洋预报精度的方法，包括如下步骤：
19.1)将初始场猜测值和外界强迫场分别加上扰动值形成集合样本，根据所述的集合样本改写解析四维集合变分的演化方程，并展开扰动量直至递推到初始时刻；包括：
20.设定动力系统在第0时刻以初始场猜测值x0为初始场开始演化，演化方程为：
21.i大于1(1)
22.式中，x
i-1
为第(i-1)时刻的状态变量，xi为第i时刻的状态变量，m
(i-1)
→i为从时刻(i-1)到时刻i的演化算符；按照演化方程递推得到如下方程
[0023][0024]
式中，m0→1为从第0时刻演化算符；f0→1为第0时刻的外界强迫场。
[0025]
在初始场猜测值x0上叠加一个猜测值扰动得到一个新的初始场猜测值在每个时刻的外界强迫场f
(i-1)
→i上叠加一个强迫场扰动得到一个新的外界强迫场形成新的集合样本，于是演化方程为：
[0026][0027]
将各个时刻状态变量xi表示为原状态变量xi与状态变量扰动量相加的形式，于是演化方程变为：
[0028][0029]
式中，为(i-1)时刻的状态变量扰动量；
[0030]
取单个积分步长为0.01，当积分时间小于72个积分步长时，公式(4)对状态变量扰动量～xi展开，并忽略高阶项，得到：
[0031][0032][0033]
将公式(6)一直递推到初始时刻得到：
[0034][0035]
式中，为(i-1)时刻新的状态变量从时刻(i-1)到时刻i的演化算符；为初始时刻的猜测值从时刻0到时刻1的演化算符；为1时刻新的状态变量从时刻1到时刻2的演化算符；为2时刻新的状态变量从时刻2到时刻3的演化算符；为时刻0到时刻1的强迫场扰动；为时刻1到时刻2的强迫场扰动；为时刻(i-2)到时刻(i-1)的强迫场扰动。
[0036]
2)当初始场猜测值与外界强迫场统计无关时，得到两个分别包含切线性演化矩阵和对应的伴随矩阵信息的特殊的背景场误差协方差矩阵；包括：
[0037]
的矩阵元素的数值虽然取决于x
i-1
的数值，根据递推关系，的矩阵元素的数值都取决于以初始场猜测值x0积分得到的状态变量值，因此，当n＜m时，定义从第n时刻到第m时刻的切线性演化矩阵为：
[0038][0039]
递推公式(7)则改写为：
[0040][0041]
式中，为新的初始场猜测值从时刻0到i时刻的演化算符；为新的初始场猜测值从时刻1到i时刻的演化算符；为新的初始场猜测值从时刻2到i时刻的演化算符。
[0042]
依据扰动量满足的公式(9)，构造第i时刻状态变量与第0时刻初始场猜测值之间的背景场误差协方差矩阵b
i0
，以及第0时刻初始场猜测值与第j时刻状态变量之间的背景场
误差协方差矩阵b
0j
；设定初始场猜测值与外界强迫场统计无关，得到
[0043][0044]
式中，b
00
为第0时刻的背景场误差协方差矩阵。
[0045]
公式(10)给出的两个特殊的背景场误差协方差矩阵，分别包含了切线性演化矩阵和对应的伴随矩阵的信息。
[0046]
3)在传统四维集合变分的基础上，对初始场猜测值附近进行扰动展开，得到未来任意时刻状态变量与切线性演化矩阵和扰动量的关系，并构建扰动后的目标函数；包括：
[0047]
在使用传统四维变分方法对初始场猜测值进行优化的时候，是使用目标函数对初始场猜测值x0求梯度，并将目标函数值和梯度值代入到最优算法中，通过线性搜索和逐步迭代得到最优的初始场。仿照传统四维变分方法对初始场猜测值进行优化的过程，在初始场猜测值x0附近进行扰动展开，得到使目标函数取极小值的最优扰动量，设扰动量为δx，对在初始场猜测值x0附近进行展开，由于扰动量是小量，忽略高阶项后得到：
[0048][0049]
则扰动后的目标函数为：
[0050][0051]
式中，xb为背景场矢量；hi为i时刻从模式网格到观测点的双线性插值投影算符；yi为i时刻观测矢量；ri为i时刻观测场误差协方差矩阵。
[0052]
4)求出扰动后的目标函数对于扰动量的梯度，具体如下：
[0053][0054]
5)在相空间按扰动量解析解的方向以设定步长进行线性搜索，更新初始场猜测值，返回步骤1)，直至扰动后的目标函数对于扰动量的梯度无限趋近于零，得到的初始场猜测值为最优的初始场猜测值；包括：
[0055]
这里利用了初始时刻与未来任意时刻之间的背景场误差协方差矩阵与这两个时刻之间的切线性演化矩阵和伴随矩阵之间的对应关系，需要指出的是，这一最优增量是在x0为初猜场的情况下得到的，对于非线性动力系统，只要稍微有一点改动，上述最优增量值就必然会发生变化，因此需要仿照传统四维变分的做法，引入线性搜索过程，即在相空间的
δx方向上，以设定的步长线性搜索使得扰动后的目标函数取极小的最优值作为δx的最优取值，从而更新初始场猜测值x0，循环步骤1)至步骤4)的过程，从而获得最优的初始场猜测值x0；将得到的最优初始场猜测值x0代入lorenz-63模型中进行预报，提高预报精度。相对传统四维变分预报精度提高效果如图2，图3和图4所示。