高精度三维轮廓控制方法及装置与流程

本发明涉及三维轮廓控制方法，尤其涉及高精度三维轮廓控制方法和装置。

背景技术：

高速高精度加工技术在现代制造业中起着关键的作用，例如数控机床CNC金属切割、激光加工等。随着三维加工需求的增加，越来越多的设备将用于三维加工，比如三轴数控机床的金属切割、串联机器人的三维焊接和激光切割等。轮廓误差指系统当前实际反馈位置与理想轮廓轨迹的最短距离，在三维轮廓控制中，轮廓误差控制的好坏是衡量产品加工质量的核心指标。

现有的轮廓控制方法可以分为两大类：间接法和直接法。

在间接法中没有一个直接和轮廓误差对应的控制量，往往是通过降低伺服系统每个单轴的跟踪误差或者提高多轴伺服系统的同步性来间接的减小轮廓误差。

在直接法中，应用最多的是交叉耦合控制和基于坐标系变换的轮廓控制。

交叉耦合控制在原有的多个单轴控制回路基础上增加了一个轮廓误差控制回路，通过对单轴跟踪误差进行交叉耦合计算得到估计的轮廓误差，然后设计轮廓误差控制器并将控制量通过交叉耦合增益分配给原有的单轴控制回路。

中国发明专利《一种复杂轨迹的轮廓控制方法》(专利号：200710030228.5)和《基于预测控制和交叉耦合的直驱XY平台轮廓控制方法》(专利号：201210359218.7)针对两轴伺服系统，使用的是交叉耦合控制的方法，在单轴控制的基础上，直接补偿系统的轮廓误差，提高加工精度。

基于坐标系变换的方法，通过将加工中的轨迹进给运动(沿着参考轮廓轨迹进行运动)和轮廓跟踪运动(与轨迹跟踪运动方向垂直的运动)进行解耦，当做两个独立的控制量来分别进行控制。

中国发明专利《基于任务极坐标系的伺服系统轮廓控制方法》(申请号：201310749851.1)，对于二维轮廓加工，通过在期望轨迹处的密切圆建立一个任务极坐标系，通过密切圆估算出当前实际位置到密切圆的最短位置，将密切圆的径向作为轮廓性能指标，将密切圆的跟踪角度作为进给性能指标，从而将轮廓性能和进给性能进行解耦控制。

以上专利中所用的方法都是针对XY两轴伺服系统进行二维轮廓控制。对于二维轮廓控制，由于轮廓误差和跟踪误差都在密切平面内，可以很方便的实现轮廓性能和进给性能的解耦。但是对于三维轮廓控制，轮廓误差往往不在密切平面内，所以对于三维轮廓控制，要实现轮廓性能和进给性能的解耦就需要在三维坐标系的每一个坐标方向进行控制，也就是需要对三组参数进行调节，参数调节繁琐，增加了三维轮廓控制方法的应用难度。

技术实现要素：

为了解决现有三维在三维轮廓控制应用中参数调节繁琐的问题，本发明提出了一种新的基于任务坐标系的方法，在新的任务坐标系下，只需要调节两组控制参数即可实现三维加工的轮廓性能和进给性能的解耦控制。

根据本发明的第一方面，提供了高精度三维轮廓控制方法，包括以下步骤：

S1、在世界坐标系F_w下建立三轴运动平台的系统动力学方程，所述三轴运动平台的三个轴互为正交轴；

S2、在期望三维轮廓w_d的当前给定点建立任务坐标系F_f，并计算世界坐标系F_w到任务坐标系F_f的坐标变换关系；

S3、通过刚体变换将任务坐标系F_f进行二次坐标变换，得到新的任务坐标系F_p，并计算任务坐标系F_f到新的任务坐标系F_p的坐标变换关系；

S4、将世界坐标系F_w下的系统动力学方程转换为新的任务坐标系F_p下的系统动力学方程；

S5、根据新的任务坐标系F_p下的系统动力学方程，设计基于反馈补偿的PD控制器，实现对误差动力学的解耦控制。

作为本发明上述方法的进一步改进，步骤S1中的所述世界坐标系用笛卡尔坐标系表示。

作为本发明上述方法的进一步改进，步骤S1中的所述系统动力学方程用惯量J、阻尼B、驱动器增益K、系统实际反馈位置w和系统的轮廓控制器输出电压u表示，为：

其中，J，B，K∈R^3×3，是常数对角矩阵，w和u是三维向量。

作为本发明上述方法的进一步改进，可对上述系统动力学方程进行拉普拉斯变换，得到从系统的轮廓控制器输出电压u到系统各轴输出速度之间的传递函数，所述传递函数为一阶惯性模型，并对系统各轴进行单独辨识，从而得到所述一阶惯性模型的参数。

作为本发明上述方法的进一步改进，在步骤S2中，根据所述期望三维轮廓w_d的曲率、挠率信息来建立当前给定点的任务坐标系F_f，所述任务坐标系F_f的三个正交基表示如下：

其中t，n和b分别代表任务坐标系F_f的单位切向量，单位法向量和单位副法向量，和分别代表世界坐标系下期望三维轮廓w_d的一阶和二阶导数。

作为本发明上述方法的进一步改进，在步骤S3中，所述新的任务坐标系F_p的法向量方向即为轮廓误差向量方向，并且所述新的任务坐标系F_p的密切平面经过轮廓误差向量和期望三维轮廓w_d的当前给定点。

作为本发明上述方法的进一步改进，所述步骤S4包括以下步骤：

S41、将世界坐标系F_w下的系统动力学方程转换为任务坐标系F_f下的系统动力学方程；

S42、将任务坐标系F_f下的系统动力学方程转换为新的任务坐标系F_p下的系统动力学方程。

作为本发明上述方法的进一步改进，所述步骤S5包括以下步骤：

S51、设计耦合非线性部分对所述系统进行补偿；

S52、通过系统进给方向上的误差和轮廓方向上的误差，设计PD控制器来实现系统的渐进稳定；

S53、得到新的任务坐标系F_p下系统的轮廓控制器输出电压u_p；

S54、将新的任务坐标系F_p下系统的轮廓控制器输出电压u_p转换到世界坐标系F_w下，得到世界坐标系F_w下系统各轴所需的轮廓控制器输出电压u，从而实现基于反馈补偿的PD控制器来对误差动力学的解耦控制。

根据本发明的第二方面，提供高精度三维轮廓控制装置，包括计算机、实时控制器、伺服驱动器和三轴运动平台，其中：

所述三轴运动平台能沿三个正交轴方向进行运动；

所述实时控制器配置为使用输出电压来实时控制三轴运动平台沿各个轴的运动；

所述伺服驱动器配置为将三轴运动平台在进给方向上的误差和轮廓方向上的误差反馈给实时控制器，从而反馈调节三轴运动平台沿各个轴的运动；

所述计算机配置为计算上述任一项权利要求中的计算式，以及发送和接收来自实时控制器的指令。

本发明的有益效果是：在三维轮廓控制中，基于本发明提出的任务坐标系，能够实现三维轮廓的进给性能和轮廓性能的解耦控制；在本发明中，只需要调节两组参数就可以分别控制三维的轮廓性能和进给性能，能够大大简化三维轮廓控制器的设计难度和控制器参数调节的复杂度，并有效提高三维轮廓的控制精度。

附图说明

图1为根据本发明高精度三维轮廓控制方法的一个实施例的总体流程图；

图2为根据本发明高精度三维轮廓控制方法的一个实施例的系统结构图；

图3为本发明高精度三维轮廓控制方法中新的任务坐标系示意图；

图4为根据本发明高精度三维轮廓控制方法的一个实施例中步骤S4的流程图；

图5为根据本发明高精度三维轮廓控制方法的一个实施例中步骤S5的流程图；

图6为根据本发明高精度三维轮廓控制方法的一个实施例中三维轮廓控制器的结构图；

图7为本发明高精度三维轮廓控制装置的一个实施例中的结构组成示意图。

具体实施方式

以下结合附图说明及具体实施方式对本发明作进一步说明。

根据本发明的一个实施例，提供了高精度三维轮廓控制方法，如图1所示所述方法包括以下步骤：

S1、在世界坐标系F_w下建立三轴运动平台的系统动力学方程，所述三轴运动平台的三个轴互为正交轴；

S2、在期望三维轮廓w_d的当前给定点建立任务坐标系F_f，并计算世界坐标系F_w到任务坐标系F_f的坐标变换关系；

S3、通过刚体变换将任务坐标系F_f进行二次坐标变换，得到新的任务坐标系F_p，并计算任务坐标系F_f到新的任务坐标系F_p的坐标变换关系；

S4、将世界坐标系F_w下的系统动力学方程转换为新的任务坐标系F_p下的系统动力学方程；

S5、根据新的任务坐标系F_p下的系统动力学方程，设计基于反馈补偿的PD控制器，实现对误差动力学的解耦控制。

上述实施例中的世界坐标系可以用笛卡尔坐标系、球坐标系或极坐标系等任一种坐标系表示，但作为上述实施例的优选实施例，步骤S1中的所述世界坐标系用笛卡尔坐标系表示。

作为上述实施例的进一步改进，步骤S1中的所述系统动力学方程可用惯量J、阻尼B、驱动器增益K、系统实际反馈位置w和系统的轮廓控制器输出电压u表示，为：

其中，J，B，K∈R^3×3，是常数对角矩阵，w和u是三维向量。

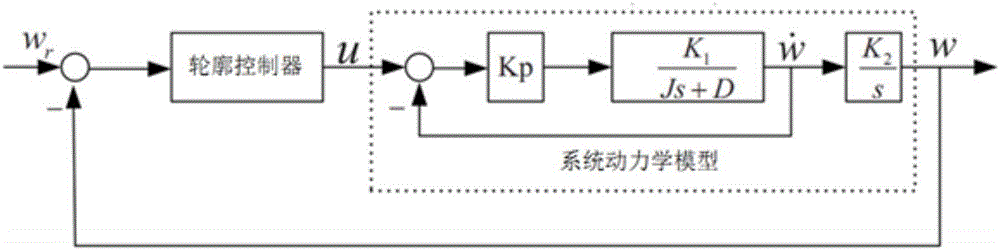
作为上述实施例的进一步改进，可对上述系统动力学方程进行拉普拉斯变换，得到从系统的轮廓控制器输出电压u到系统各轴输出速度之间的传递函数，即系统动力学模型，所述传递函数为一阶惯性模型，如图2中虚线框所示。图2中，K_p代表速度环比例控制器增益值，J代表机械被控对象的转动惯量，s代表拉普拉斯算子，D代表机械被控对象的粘滞摩擦系数，K₁代表机械被控对象的放大增益，K₂代表机械被控对象由转动到平移运动的积分增益，代表机械被控对象的实际角速度，w代表机械被控对象的实际反馈位置。然后可以通过笛卡尔坐标系下期望指令的给定值w_r，对系统动力学方程的各个参数J、B、K进行辨识，优选地，采用扫频的方法，对系统各轴进行单独辨识，由系统的轮廓控制器产生频率连续可变的模拟量速度输入信号，分别输入到三轴运动平台的各个轴，如机床的X轴、Y轴和Z轴，在得到三个轴的速度输出后，可通过Matlab的系统辨识工具箱对进行拟合从而得到所述一阶惯性模型的参数。

作为上述实施例的进一步改进，在步骤S2中，根据所述期望三维轮廓w_d的曲率、挠率信息来建立当前给定点的任务坐标系F_f，所述任务坐标系F_f的三个正交基表示如下：

其中t，n和b分别代表任务坐标系F_f的单位切向量，单位法向量和单位副法向量，和分别代表世界坐标系下期望三维轮廓上点的坐标值w_d的一阶和二阶导数。若定义任务坐标系F_f到世界坐标系F_w之间的坐标变换为T_fw，其逆变换T_fw，则其间的坐标变换公式可表示如下：

T_fw：w＝Rf_F+w_d (3)

T_wf：f_F＝R^-1(w-w_d) (4)

其中，f_F代表任务坐标系下期望轨迹上点的坐标值，R＝[t，n，b]代表坐标变换矩阵，并且R^-1＝R^T。

作为上述实施例的进一步改进，在步骤S3中，建立如图3所示的新的任务坐标系，所述新的任务坐标系F_p的法向量方向即为轮廓误差向量方向，并且所述新的任务坐标系F_p的密切平面经过轮廓误差向量和期望三维轮廓w_d的当前给定点。若定义新的任务坐标系F_p到任务坐标系F_f和之间的坐标变换为T_pf，其逆变换为T_fp，则其间的坐标变换公式可表示如下：

T_pf：f_F＝F_fp+f_{F_E} (5)

T_fp：f_p＝F^-1(f_F-f_{F_E}) (6)

其中，J_F代表任务坐标系下期望三维轮廓上点的坐标值，J_{F_E}代表任务坐标系下期望三维轮廓上距离当前实际反馈位置最近点的坐标，J_p代表新的任务坐标系下期望三维轮廓上点的坐标值。F代表两个坐标系之间坐标变换矩阵，并且F^-1＝F^T。

作为上述实施例的进一步改进，如图4所示所述步骤S4可包括以下步骤：

S41、将世界坐标系F_w下的系统动力学方程转换为任务坐标系F_f下的系统动力学方程。世界坐标系F_w下的系统动力学方程如(1)式所示，将(3)式代入(1)式，可将在世界坐标系F_w下的系统动力学方程转换到任务坐标系F_f下，得到：

其中M_F＝JR，和

S42、将任务坐标系F_f下的系统动力学方程转换为新的任务坐标系F_p下的系统动力学方程。通过将(5)式代入(7)式，将在任务坐标系F_f下的系统动力学方程转换到新的任务坐标系F_p下，得到：

其中M_P＝M_FF，

作为上述实施例的进一步改进，如图5所示所述步骤S5可包括以下步骤：

S51、设计耦合非线性部分对所述系统进行补偿。根据新的任务坐标系下期望三维轮廓上点的坐标值J_p，所述耦合非线性部分可设计为

S52、通过系统进给方向上的误差和轮廓方向上的误差，设计PD控制器来实现系统的渐进稳定。根据在新的任务坐标系F_p下的系统动力学方程，可选取状态变量如下：

其中表示进给方向上的误差，表示轮廓方向上的误差，z₃＝0。则PD控制器可表示为V(Z₁，Z₂)：

V(Z₁，Z₂)＝-K_pZ₁-K_dZ₂ (11)

其中K_p为速度环比例控制器增益值，K_d为微分系数。且由(8)式可得到新的任务坐标系F_p下的系统实际反馈位置的二阶导数为：

S53、得到新的任务坐标系F_p下系统的轮廓控制器输出电压u_p，根据耦合非线性部分的设计以及以上各式，可取u_p为：

将(13)式代入到(12)式，可得：

由(10)得到Z₂的一阶导数为：

将(14)式代入(15)式得：

将(11)式代入(16)式得：

其中

由(18)式和(19)式可以看出，在新的任务坐标系F_p下，通过调节(18)和(19)中的参数和即可解耦控制系统的进给性能和轮廓性能。图6显示了这一实施例中系统的控制器框图。

S54、将新的任务坐标系F_p下系统的轮廓控制器输出电压u_p转换到世界坐标系F_w下，得到世界坐标系F_w下系统各轴所需的轮廓控制器输出电压u：

从而实现基于反馈补偿的PD控制器来对误差动力学的解耦控制。其中，进一步实现只需要调节两个参数即可调节系统实际反馈位置w。

根据本发明另一实施例，提供高精度三维轮廓控制装置，包括计算机、实时控制器、伺服驱动器和三轴运动平台，其中：

所述三轴运动平台能沿三个正交轴方向进行运动；

所述实时控制器配置为使用输出电压来实时控制三轴运动平台沿各个轴的运动；

所述伺服驱动器配置为将三轴运动平台在进给方向上的误差和轮廓方向上的误差反馈给实时控制器，从而反馈调节三轴运动平台沿各个轴的运动；

所述计算机配置为计算上述任一项权利要求中的计算式，以及发送和接收来自实时控制器的指令。

图7显示本发明高精度三维轮廓控制装置的一个实施例，其由PC机1、实时控制器2、伺服驱动器3和三轴数控机床本体4。

本发明的系统动力学方程也可以在时域上建立，这时添加时域的系统动力学方程为：

其中，F是三维的库伦摩擦力向量，和速度方向相反，当速度为正时，库伦摩擦力为负的常数，当速度为负时，库伦摩擦力为正的常数。其它参数的含义参照上述。根据上述(1)式到(20)式同样的方法，可以实现只需要调节两个参数即可实时调节系统实际反馈位置w(t)。

本发明通过在期望三维轮廓的轮廓误差位置处建立一个新的任务坐标系，该新的任务坐标系的法向量方向即为轮廓误差向量方向，并且该新的任务坐标系的密切平面经过轮廓误差向量和期望三维轮廓在当前时刻的给定点。通过坐标变换将三维在世界坐标系下的系统动力学方程变换到新的任务坐标系下，并设计基于前馈补偿的反馈比例-微分(PD)控制器，实现对三维误差动力学的解耦控制。在三维的轮廓控制中，基于新的任务坐标系，能够实现三维的轮廓性能和进给性能的解耦，并且只需要调节两组参数就可以分别控制三维的轮廓性能和进给性能，能够大大简化三维轮廓控制器的设计难度和控制器参数调节的复杂度，有效提高三维轮廓的控制精度。

以上所述，只是本发明的较佳实施例而已，本发明并不局限于上述实施方式，只要其以相同的手段达到本发明的技术效果，都应属于本发明的保护范围。在本发明的保护范围内其技术方案和/或实施方式可以有各种不同的修改和变化。即使个别的技术特征在不同的权利要求中引用，本发明还可包含共有这些特征的实施例。

上述虽然结合附图对本发明的具体实施方式进行了描述，但并非对本发明保护范围的限制，所属领域技术人员应该明白，在本发明的技术方案的基础上，本领域技术人员不需要付出创造性劳动即可做出的各种修改或变形仍在本发明的保护范围以内。