滑模观测器的分布式控制系统执行器故障重构方法、观测器和设备与流程

本技术涉及控制系统故障重构，尤其涉及基于二阶非奇异快速终端滑模观测器的分布式控制系统执行器故障重构。

背景技术：

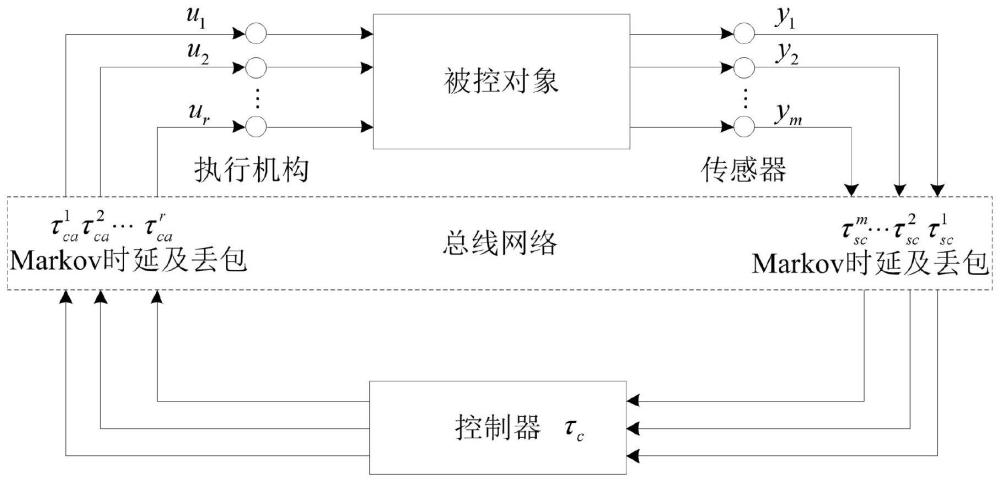
1、分布式控制系统是未来航空发动机控制系统的主要发展方向，与目前航空发动机集中式控制系统的“点对点”连接方式(图1)不同，在分布式控制系统(图2)中，中央控制器与分布式智能节点间的信息传输是通过数据总线来完成的，中央控制器主要实现高级处理功能，例如，系统的控制计划、系统状态监测、高级控制算法计算以及数据总线仲裁方案选取等，而低级功能如信号采集、软硬件自测试、数据信号的解调/解码以及冗余管理等都下放到智能传感器与智能执行器中。采用分布式的通讯网络方式、智能传感器以及智能执行器，可以大幅减轻控制系统的重量，大幅提高控制系统性能与可靠性，同时减少了系统的研发费用与周期。分布式架构和网络总线的引入为分布式控制系统带来上述优点的同时，也带来了新的困难与挑战。一方面，系统结构随着总线的引入发生彻底改变，总线传输过程中的网络不确定性因素严重影响了控制系统性能；另一方面，系统中的各种不确定外部干扰因素对带有网络因素的系统动静态性能影响更为严重。例如，在航空发动机分布式控制系统中，随着发动机性能与功能要求的提高，整个系统闭环回路处理的信息数据量也越来越多，导致总线网络承载能力、带宽以及服务能力有限，不可避免的会产生网络因素以及外部扰动不确定性等问题，对发动机的运行产生一定的影响。

2、对于分布式控制系统中存在的网络不确定性问题主要有：网络诱导时延、数据包丢失、多包传输以及网络节点驱动方式等。除了这些由于网络总线引入产生的共性问题外，在航空发动机分布式控制系统中同样面临着传感器与执行器故障的问题，由于系统中的智能传感器与执行器功能的增加，相应的智能微处理器、总线接口以及数据收发器等部件随之增多，另外某些智能节点工作于高温、高压以及高频振动等环境中，这使得智能节点极易出现故障情况。这些故障的发生将会影响系统中数据的传输，从而严重影响了整个系统的动静态性能，给发动机正常运转和飞机飞行带来重大安全隐患。因此，有必要针对航空发动机分布式控制系统，设计合理的故障诊断方法对系统中的故障进行估计并准确定位。

3、考虑滑模变结构控制具有优良的鲁棒特性，滑模观测器的应用不仅能够提高故障重构信号的效果，同时滑模运动对控制系统的未建模动态特性、输入、输出扰动和参数摄动等问题具有不变性，所以滑模控制理论用于分布式控制系统故障诊断和重构等问题的解决，具有十分重要的理论意义和应用价值。基于滑模观测器解决分布式控制系统故障重构问题时，滑模观测器的高频切换控制输入项ν一定程度上增加了仿真计算的负担，通常利用经过平滑处理后的输入项对ν(t)进行调整，但实际上这是一种伪滑模控制。如果直接采用连续的切换信号，这时滑模的高频抖振会给故障重构的精度以及误差系统收敛性能带来影响，对于某些幅值很小的故障重构结果影响更为明显。解决高频抖振问题最好的办法是采用高阶滑模控制策略，该方法是在滑模控制变量的高阶次导数中设计高频控制输入项，再引入连续的输出注入信号，从而达到降低系统中高频抖振影响的目的。有关终端滑模与高阶滑模设计方法的结合，目前已取得了一系列研究成果，另外，在二者结合的基础上，考虑非奇异快速性问题，对滑模控制器的收敛速率问题国内外也有相关的研究。但是，这些方法在解决故障重构问题方面却鲜有报道，而在分布式控制系统中，网络诱导时延也是影响重构效果的一个重要因素，所以将高阶终端滑模与非奇异快速终端滑模观测器综合应用于分布式控制系统的故障重构问题中，需要考虑时延不确定性因素对故障重构结果的影响。

技术实现思路

1、本发明目的是为了解决因网络诱导时延等网络不确定性的影响，导致滑模观测器的分布式控制系统执行器故障重构效率和准确度低的问题，提供了滑模观测器的分布式控制系统执行器故障重构方法、观测器和设备。

2、本发明是通过以下技术方案实现的，本发明一方面，提供一种滑模观测器的分布式控制系统执行器故障重构方法，所述方法包括：

3、步骤1、建立分布式控制系统模型：

4、

5、其中，z1，z2为系统两个状态变量，y为控制输出，a∈rn×n,b∈rn×m,c∈rp×n,e∈rn×q,d∈rn×l分别为适维矩阵，且满足条件n＞p≥q和l，f(t)为控制系统的执行器故障向量，矩阵为状态反馈控制器的控制增益，li为满足条件li＝[li1|0]的适维矩阵，时延τ为时变有界的markov随机变量，t为当前时刻，ξ(t)为未知扰动等不确定向量，

6、步骤2、建立含自适应律的高阶快速非奇异终端滑模观测器，具体包括：

7、建立二阶快速非奇异终端观测器：

8、

9、其中，和为系统状态量估计值，ν(t)为二阶的滑模控制输入项，通过满足(a22-a21li)-k是hurwitz矩阵的条件，可以求出矩阵k数值；

10、定义误差得控制系统的误差方程为：

11、

12、令e2＝ζ，ω(t)＝-ν(t)，

13、π(e1,e2,t)＝a21e1(t)+(a22-a21li-k)e2(t)+aτ21e1(t-τ)+(aτ22-aτ21li)e2(t-τ)+e2f(t)+d2ξ(t)

14、

15、

16、非奇异快速终端滑模控制的滑模面为：

17、

18、其中，α、β、λ、σ为待设计的滑模面系数，λ和σ是正奇数且有1＜λ/σ＜2，β＞0；

19、步骤3、当误差系统到达所设计的非奇异快速终端滑模面上时，结合控制输入项对故障信号进行估计，得出故障信号重构值。

20、进一步地，步骤1之前还包括前提假设：

21、假设1、分布式控制系统中的控制器为事件驱动方式，智能传感器节点与执行器节点为时钟驱动方式；

22、假设2、时延和均有上界，数据带有时间戳，传输过程为单包传输，且不存在时序错乱的现象；其中，为第i个传感器到控制器时延，即第i个控制时延，第i个控制器到执行器时延，即第i个输出时延，r为传感器到控制器时延总个数，m为控制器到执行器时延总个数；

23、假设3、当存在数据丢包时，沿用上一采样时刻数据；

24、假设4、每个传感器到控制器的时延τsc大小都相同，控制器到所有执行器的时延τca大小同样假设相同；定义系统总时延为τ(t)，总控制时延为τca(t)，总输出时延τsc(t)，结合假设1、假设2，得出τ(t)为τca(t)与τsc(t)之和，即τ(t)＝τca(t)+τsc(t)，其中，t为当前时刻；考虑系统在某一时段的时延情况与此时的总线负载情况有关，将时延序列{τ(t)0＜τ(t)≤τm(t),t＝0,1,…}等效为有限状态的markov过程；假设τ(t)＝3，τ(t)的状态空间为ω＝{1,2,3}，其转移概率矩阵π＝πij,(i,j∈ω)由下式确定：

25、

26、其中δt＞0，πij≥0(i,j∈ω,i≠j)是系统在t时刻处于时延i，而在时刻t+δt取时延j的转移率；对任意时延有

27、假设5、定义f＝[d e]，(a，c，f)中不变零点均在左半开复平面内，即当条件rankf＝q+l满足时，有成立；

28、其中，矩阵a∈rn×n,c∈rp×n,e∈rn×q,d∈rn×l为状态空间矩阵，f矩阵由矩阵d，e组成，即f＝[d e]，式中，n,p,q,l为对应矩阵的行数和列数，s为常数；

29、假设6、系统满足匹配条件，即rank(cf)＝rank(f)；

30、假设7、执行器故障f(t)有界且δ为执行器故障倒数的上界值，是一个未知的常数；ξ(t)有界且μ为未知扰动等不确定向量导数的上界值，是一个已知常数，f(t)为控制系统的执行器故障向量，ξ(t)为未知扰动等不确定向量。

31、进一步地，采用步骤2中的非奇异快速终端滑模控制的滑模面，所述自适应快速终端滑模观测器的控制输入为：

32、ω(t)＝ω1(t)+ω2(t)+ω3(t)+ω4(t)

33、ω1(t)＝-k0ζ-(aτ22-aτ21li)e2(t-τ)

34、

35、

36、

37、其中，sgn为符号函数，k0、k10、k2为待设计参数，k10(t)为设计的自适应律，ρ＞0为自适应增益项。

38、进一步地，步骤3中，所述故障信号重构值的获取方法，具体包括：

39、满足有如下等式成立：

40、a21e1(t)+aτ21e1(t-τ)+e2f(t)+d2ξ(t)-ν(t)＝0

41、当ιm(e2)∩ιm(d2)＝{0}时，存在矩阵w使得h1，h2为适维矩阵，由于|e1|有界稳定，则有：

42、

43、选取矩阵w1为矩阵w的前q行，得到：

44、

45、其中，为控制系统的执行器故障信号重构值。

46、进一步地，步骤3中，所述故障信号重构值的获取方法，具体包括：

47、当ιm(e2)∩ιm(f2)≠{0}时，其中，式中，(e2)+为e2的伪逆矩阵。

48、进一步地，故障重构误差为：

49、

50、其中，||ef(t)||≤||(e2)+||(a21e1(t)+aτ21e1(t-τ)+||d2||ξ(t))；

51、假设误差e1(t)导数上界为θ，即有：

52、||ef(t)||≤||(e2)+||[θ(||a21||+||aτ21||)+||d2||ξ(t)]。

53、第二方面，本发明提供一种高阶快速非奇异终端滑模观测器，所述观测器为针对如上文所述的分布式控制系统模型所设计，所述观测器具体为：

54、

55、式中，和为系统状态量估计值，ν(t)为二阶的滑模控制输入项，通过满足(a22-a21li)-k是hurwitz矩阵的条件，可以求出矩阵k数值；

56、误差控制系统的误差方程为：

57、

58、e2＝ζ，ω(t)＝-ν(t)，

59、π(e1,e2,t)＝a21e1(t)+(a22-a21li-k)e2(t)+aτ21e1(t-τ)+(aτ22-aτ21li)e2(t-τ)+e2f(t)+d2ξ(t)

60、

61、

62、非奇异快速终端滑模控制的滑模面为：

63、

64、式中，α、β、λ、σ为待设计的滑模面系数，λ和σ是正奇数且有1＜λ/σ＜2，β＞0，

65、二阶快速非奇异终端观测器的控制输入为：

66、ω(t)＝ω1(t)+ω2(t)+ω3(t)+ω4(t)

67、ω1(t)＝-k0ζ-(aτ22-aτ21li)e2(t-τ)

68、

69、

70、

71、式中，sgn为符号函数，k0、k10、k2为待设计参数，k10(t)为设计的自适应律，如下式所示：

72、

73、其中，ρ＞0为自适应增益项。

74、第三方面，本发明提供一种计算机设备，包括存储器和处理器，所述存储器中存储有计算机程序，当所述处理器运行所述存储器存储的计算机程序时执行如上文所述的一种滑模观测器的分布式控制系统执行器故障重构方法的步骤。

75、第四方面，本发明提供一种计算机可读存储介质，所述计算机可读存储介质中存储有多条计算机指令，所述多条计算机指令用于使计算机执行如上文所述的一种滑模观测器的分布式控制系统执行器故障重构方法。

76、第五方面，本发明提供一种电子设备，包括：

77、至少一个处理器；以及，

78、与所述至少一个处理器通信连接的存储器；其中，

79、所述存储器存储有可被所述至少一个处理器执行的指令，所述指令被所述至少一个处理器执行，以使所述至少一个处理器能够执行如上文所述的一种滑模观测器的分布式控制系统执行器故障重构方法。

80、本发明的有益效果：

81、为有效解决带有网络诱导时延分布式控制系统执行器故障重构的问题，本发明提供了一种基于二阶非奇异快速终端滑模观测器的故障重构算法。可以有效降低高频抖振对执行器故障重构的影响，能够克服网络诱导时延等网络不确定性的影响，实现对变化率上界未知执行器故障信号的快速准确重构，相比于采用非奇异终端滑模面的观测器，状态估计误差收敛速度更快，与一阶滑模观测器相比，可以降低切换项中的抖振影响，实现高性能、无抖振的状态跟踪。

82、总体而言，本发明具有如下优点：

83、1.设计了一种二阶非奇异快速终端滑模面，与一阶滑模观测器相比，可以降低切换项中的抖振影响，实现高性能、无抖振的状态跟踪，有效降低了高频抖振对执行器故障重构的影响。

84、2.本发明能够有效克服网络诱导时延对分布式控制系统故障重构的影响，实现对变化率上界未知执行器故障信号的快速准确重构。

85、3.所构建的观测器相比于非奇异终端滑模面的观测器，状态估计误差收敛速度更快。在一定程度上提高了分布式控制系统工作效率，降低了成本，同时也提高了系统的稳定性和安全性。

86、本发明提出的基于二阶非奇异快速终端滑模观测器的执行器故障重构算法，可有效实现航空发动机分布式控制系统执行器故障重构，效率高，成本低，对于硬件要求不算苛刻，具有一定的应用意义，可广泛应用于一类带有网络诱导时延的分布式控制系统的故障重构问题。