基于输入受限的自适应滑模有限时间船舶轨迹跟踪控制方法

本发明涉及船舶运动控制，尤其涉及一种基于输入受限的自适应滑模有限时间船舶轨迹跟踪控制方法。

背景技术：

1、随着社会的发展，货物来往愈加频繁，而海运作为国际贸易中最主要的运输方式，更是发挥着重要作用，所以，船舶的地位和作用也变得越来越重要。船舶，它不仅是海洋运输的重要工具，还承载着国际贸易和经济发展的重要使命，是世界经济发展的重要支柱。船舶轨迹跟踪控制是指通过控制器的设计使得船舶按照期望轨迹进行航行，其目的在于促进船舶走向智能化，保障航行安全，为航海人员减轻负担。船舶自身有着非线性、强耦合性、大惯性等特点，导致往往难以获取精确的数学模型，且船舶所处海况较为复杂，易受外界未知干扰的影响。因此，如何有效抵抗未知干扰影响，提高船舶的轨迹跟踪速率和安全则成为了当前船舶运动控制领域的研究热点。

2、目前船舶航行在海上，将会面临着各种内外部的干扰，外部干扰表现为风浪流作用于船舶所导致的偏移、变速以及摇晃等情况。内部扰动则是由于货物装卸、燃油和食物等各种消耗所导致的船舶参数发生变化所引起的模型不确定性。因此，在设计控制器时应考虑内外部扰动。同时，使船舶在跟踪至期望轨迹的过程中拥有更快的收敛速率也一直是船舶运动控制领域的研究热点。控制输入的增大必然使得控制输入变大，但由于船舶执行机构的固有特性，控制输入会存在着一定的界限。而过大的输入量可能会导致执行器故障，系统震荡，甚至引起系统失衡，因此，在考虑加快收敛速率的同时考虑输入饱和是非常有必要的。

技术实现思路

1、本发明提供一种基于输入受限的自适应滑模有限时间船舶轨迹跟踪控制方法，以克服上述技术问题。

2、为了实现上述目的，本发明的技术方案是：

3、一种基于输入受限的自适应滑模有限时间船舶轨迹跟踪控制方法，包括以下步骤：

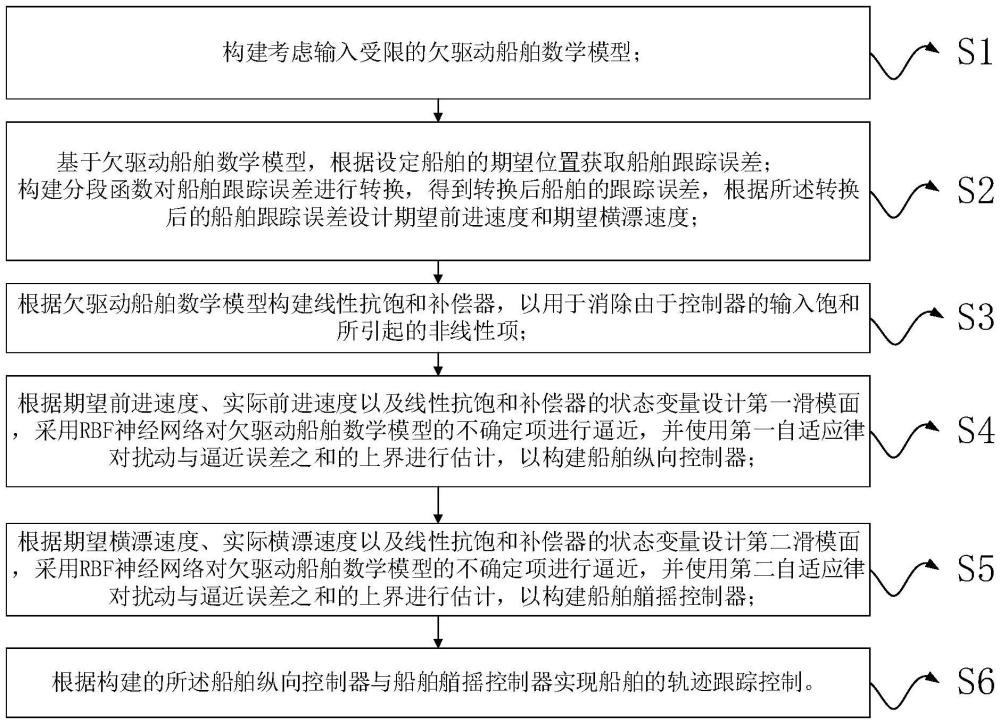
4、s1：构建考虑输入受限的欠驱动船舶数学模型；

5、s2：基于欠驱动船舶数学模型，根据设定船舶的期望位置获取船舶跟踪误差；

6、构建分段函数对船舶跟踪误差进行转换，得到转换后船舶的跟踪误差，根据所述转换后的船舶跟踪误差设计期望前进速度和期望横漂速度。

7、s3：根据欠驱动船舶数学模型构建线性抗饱和补偿器，以用于消除由于控制器的输入饱和所引起的非线性项；

8、s4：根据期望前进速度、实际前进速度以及线性抗饱和补偿器的状态变量设计第一滑模面，采用rbf神经网络对欠驱动船舶数学模型的不确定项δfu进行逼近，并使用第一自适应律对扰动与逼近误差之和的上界进行估计，以构建船舶纵向控制器；

9、s5：根据期望横漂速度、实际横漂速度以及线性抗饱和补偿器的状态变量设计第二滑模面，采用rbf神经网络对欠驱动船舶数学模型的不确定项δfr进行逼近，并使用第二自适应律对扰动与逼近误差之和的上界进行估计，以构建船舶艏摇控制器；

10、s6：根据构建的所述船舶纵向控制器与船舶艏摇控制器实现船舶的轨迹跟踪控制。

11、进一步的，s1中构建的考虑输入受限的欠驱动船舶数学模型的表达式为

12、

13、δτu＝τu-τu1

14、δτr＝τr-τr1

15、式中：x,y,ψ分别表示船舶的前进位移、横漂位移以及艏向角；表示x的一阶导；表示y的一阶导；u,v,r分别表示船舶在附体坐标系下的纵向速度、横向速度、艏摇角速度；τu1表示考虑限制后的船舶控制器的实际纵向控制力；τr1表示考虑限制后的船舶控制器的实际艏摇控制力矩；m11,m22,m33表示惯性参数；d11,d22,d33表示水动力参数；δfu,δfv,δfr表示船舶模型的不确定项；τwu,τwv,τwr表示外界未知扰动；τim表示控制输入的上界；τuc表示期望船舶纵向控制力；τrc表示期望艏摇控制力矩；δτu与δτr表示期望输入与实际输入之差。

16、进一步的，所述s2具体包括以下步骤：

17、s21：基于欠驱动船舶数学模型，根据设定船舶的期望位置获取船舶跟踪误差，其表达式为

18、

19、式中：xe,ye分别表示船舶前进位移的跟踪误差与船舶横漂位移的跟踪误差；xd,yd分别表示船舶期望前进位移与船舶期望横漂位移；

20、s22：构建分段函数，其表达式为

21、

22、

23、式中：kz表示分段函数；z(t)表示中间变量函数；α1,p,β1均表示正的设计参数；t表示时间参数；t表示时间的阈值参数；

24、s23：使用分段函数对所述船舶跟踪误差进行误差转化，获取船舶跟踪转换误差，其表达式为

25、

26、式中：zx,zy分别表示船舶前进位移的跟踪误差xe与船舶横漂位移的跟踪误差ye误差转换后的船舶跟踪转换误差；

27、s24：根据所述船舶跟踪转换误差设计船舶的期望前进速度与期望横漂速度，其表达式为

28、

29、式中：ud表示期望前进速度；vd表示期望横漂速度；c1,c2,c3,c4,ε1,ε2表示正的设计参数；ψ表示船舶的艏向角；表示kz的一阶导。

30、进一步的，s3中构建的所述线性抗饱和补偿器，其表达式为

31、

32、式中：k1,k2表示正的设计参数；δτ表示δτu与δτr的统称；ξ表示补偿器的状态变量，且ξ＝ξ1,ξ2；表示ξ的一阶导。

33、进一步的，所述s4具体包括以下步骤：

34、s41：根据期望前进速度、实际前进速度以及线性抗饱和补偿器的状态变量设计第一滑模面，其表达式为

35、

36、ue＝u-ud-ξ1

37、式中：s1表示第一滑模面；λ1表示正的设计参数；ue表示中间参数变量；

38、s42：对所述第一滑模面求导，并结合欠驱动船舶数学模型能够得到

39、

40、且令

41、

42、式中：wu表示rbf神经网络的权重向量；wut表示wu的转置；hu(x)表示高斯函数；o1表示逼近误差；

43、s43：根据步骤s41至s42，使用第一自适应律对未知参数wu与μ1进行估计，且所述第一自适应律的表达式为

44、

45、式中：η1,η2,σ1,σ2为正的设计参数；μ1表示中间参数变量，且μ1＝d1+o1*；表示μ1的估计值；o1*逼近误差o1的上界

46、s44：令以构建船舶纵向控制器，其表达式为

47、

48、式中：c5,c6,ε3表示正的设计参数；表示wu的估计值。

49、进一步的，所述s5具体包括以下步骤；

50、s51：根据期望横漂速度、实际横漂速度以及线性抗饱和补偿器的状态变量设计第二滑模面，其表达式为

51、

52、式中：s2表示第二滑模面；λ2表示正的设计参数；ve表示中间参数变量；

53、s52：对所述第二滑模面求导，并结合欠驱动船舶数学模型能够得到

54、

55、且令

56、δfr＝wrthr(x)+o2

57、

58、式中：wr表示rbf神经网络的权重向量；wrt表示wr的转置；hr(x)表示高斯函数；o2表示逼近误差；f表示中间参数变量；

59、且

60、其中，为了避免直接对f进行求导出现微分爆炸现象，利用动态面技术，使用一阶滤波器的输出能够避免对f直接进行求导，即引入新的变量fr并作为f的一阶低通滤波器的输出，其表达式如下

61、

62、式中：tr表示设计参数，且tr＞0；fr(0),f(0)均表示初始值；

63、s53：根据步骤s51至s52，使用第二自适应律对未知参数wr与μ2进行估计，且所述第二自适应律的表达式为

64、

65、式中：η3,η4,σ3,σ4,ε5表示正的设计参数；μ2表示中间参数变量，且μ2＝d2+o2*；表示μ2的估计值；表示wr的估计值；o2*逼近误差o2的上界

66、s54：定义中间变量

67、且令以构建船舶艏摇控制器，其表达式为

68、

69、式中：c7,c8,ε4表示为正的设计参数。

70、有益效果：本发明提供了一种基于输入受限的自适应滑模有限时间船舶轨迹跟踪控制方法，根据欠驱动船舶数学模型构建线性抗饱和补偿器，以用于消除控制器的输入饱和，即使用线性抗饱和补偿器来消除由输入饱和所引起的非线性项；同时针对考虑输入受限的欠驱动船舶数学模型内外部的干扰问题，采用rbf神经网络去逼近船舶模型的不确定项，再用自适应技术去估计逼近误差以及外界未知干扰的上界；采用自适应滑模技术并在反步法的框架下，根据设计的期望前进速度与期望横漂速度构建船舶纵向控制器与船舶艏摇控制器，以实现船舶的轨迹跟踪控制，且对于收敛速度慢的问题，将结合有限时间收敛理论进行控制器的设计，以使得误差实现有限时间收敛。