地面出入式盾构法隧道施工引起的土体垂直变形计算方法与流程

本发明属于地下工程技术领域，涉及一种地面出入式盾构法隧道施工引起的土体垂直变形计算方法。

背景技术：

地面出入式盾构法工法与传统的盾构法具有较大区别。常规盾构法施工时一般要求隧道顶部覆土深度不小于盾构机直径(地铁一般为6.2m)，但地面出入式盾构法施工存在超浅埋工况，顶部覆土深度≤5m，对浅层土体的扰动较大，故其有可能引发邻近地下管线及建筑物的破坏，存在严重的安全隐患。

林存刚^[1]结合杭州市庆春路过江盾构隧道工程，基于Mindlin解提出了盾构以一定坡度掘进时掘削面正面附加推力q和盾壳摩擦力f的竖向分力与水平分力共同引起的地面土体垂直变形计算公式。但其计算公式的坐标设定仅考虑q与f的方向与水平面的夹角β，并没有考虑盾构轴线与水平面的夹角(见图1a)，即假设盾构推进方向为水平、忽略盾构埋深变化，由此得出的计算结果与实际不符，给工程带来安全隐患。且未推导由盾尾附加注浆压力及土体损失引起的土体垂直变形计算公式。

技术实现要素：

本发明的目的是克服现有技术中不足，提供一种地面出入式盾构法隧道施工引起的土体垂直变形计算方法。

为解决该种特殊工况引起的土体垂直沉降变形计算，并为今后现场施工及其研究提供理论支持，本专利考虑了盾构轴线与水平面夹角β(即隧道埋深变化)，推导了掘削面正面附加推力、盾壳摩擦力、盾尾附加注浆压力、土体损失因素引起的地面出入式盾构法隧道施工引起的土体垂直变形计算方法。

为了达到上述目的，本发明是通过以下技术方案实现的：

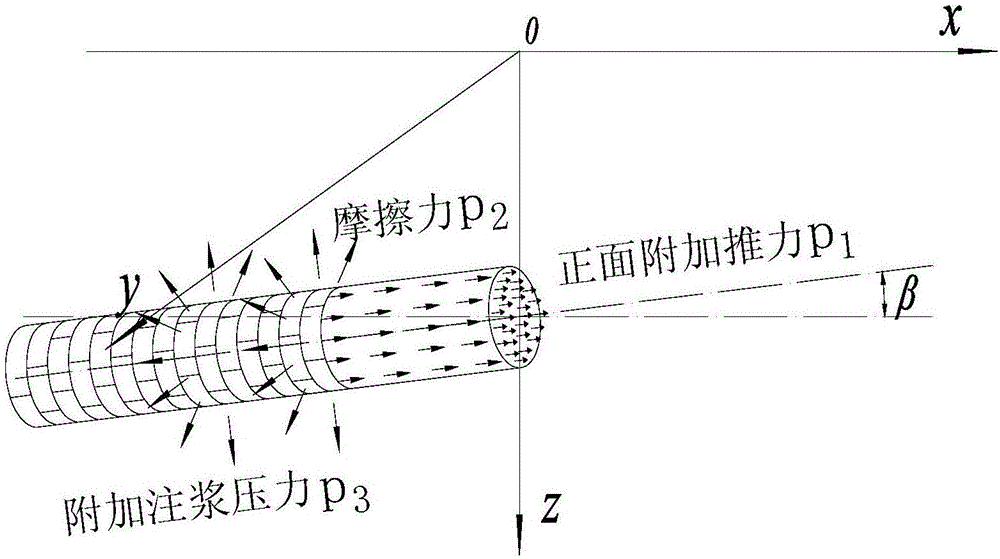
本发明提供一种地面出入式盾构法隧道施工引起的土体垂直变形计算方法，由于本发明真实考虑到盾构推进方向和各力均与水平面有一定夹角β(见图1b，以向上为正，向下为负)。分别提出掘削面正面附加推力、盾壳摩擦力、盾尾附加注浆压力以及土体损失各因素引起的土体垂直变形计算公式。

本发明力学计算模型见图2。

图中x为离开挖面的水平距离，单位符号为mm，以掘进方向为正；

y为离盾构轴线的横向水平距离，单位符号为mm；

z为盾构轴线离地面的竖向距离，单位符号为mm，以向下为正。

本专利方法具体包括如下步骤：

步骤1)、正面附加推力引起的土体垂直变形计算：

取盾构开挖面内任一微单元dA＝rdrdθ，其所受的集中力为：

dp₁＝p₁rdrdθ，

式中：

A、r、θ分别为微单元面积、半径、角度，符号单位分别为mm²、mm、°；

p₁为掘削面单位面积上的正面附加推力，单位符号为Pa；

开挖面内任一微单元坐标为：

(-rsinθsinβ，-rcosθ，h-rsinθcosβ)，

式中：

h为开挖面处盾构轴线埋深，单位符号为mm；

经过坐标变换，得到用于代入Mindlin位移解的等效坐标：x₁＝x+rsinθsinβ；y₁＝y+rcosθ；h₁＝h-rsinθcosβ；

设盾构开挖面任一微单元荷载作用点、及其关于地面的对称点，到土体沉降计算点之间的距离分别为：

$M_1=\sqrt{{x_1}^2+{y_1}^2+{(z-h_1)}^2},$

$N_1=\sqrt{{x_1}^2+{y_1}^2+{(z+h_1)}^2},$

将dp₁分解为水平力dp_1h＝p₁cosβrdrdθ和竖向力dp_1v＝p₁sinβrdrdθ，分别代入Mindlin水平和竖向位移解进行积分计算；

得到在掘削面正面附加推力的水平分力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

$w_{1h}=\frac{p_{1}cos\mathrm{\β}}{16\mathrm{\π}G(1-\mathrm{\μ})}{\∫}_0^{2\mathrm{\π}}{\∫}_0^{D/2}{x}_1\[\frac{z-h_1}{M_1^3}+\frac{(3-4\mathrm{\μ})(z-h_1)}{N_1^3}-\frac{6{\mathrm{zh}}_1(z+h_1)}{N_1^5}+\frac{4(1-\mathrm{\μ})(1-2\mathrm{\μ})}{N_1(N_1+z+h_1)}\]rdrd\mathrm{\θ},$

式中：

D为盾构机外直径，单位符号为mm；

μ为土的泊松比；

G为上的剪切弹性模量，单位符号为Pa，

E_s为土的压缩模量，单位符号为Pa；

K₀为静止土压力系数；

π为圆周率，一般取3.14；

同时，在盾构掘削面正面附加推力的竖向分力作用下，土体中任一点(x，y，z)处产生的土体垂直变形为：

$w_{1v}=\frac{p_1\sin \mathrm{\β}}{16\mathrm{\π}G(1-\mathrm{\μ})}{\∫}_0^{2\mathrm{\π}}{\∫}_0^{D/2}\[\frac{(3-4\mathrm{\μ})}{M_1}+\frac{8{(1-\mathrm{\μ})}^2-(3-4\mathrm{\μ})}{N_1}+\frac{{(z-h_1)}^2}{M_1^3}+\frac{(3-4\mathrm{\μ}){(z+h_1)}^2-2h_{1}z}{N_1^3}+\frac{6h_{1}z{(z+h_1)}^2}{N_1^5}\]rdrd\mathrm{\θ}$

因此，在盾构掘削面正面附加推力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

w₁＝w_1h+w_1v

步骤2)、盾壳摩擦力引起的土体垂直变形计算：

由于盾构机为一圆柱体，取盾壳表面任一微单元dA＝Rdldθ，其所受的摩擦力为：

dp₂＝p₂Rdldθ

式中：

R为盾构半径，单位符号为mm；

l为微单元长度，单位符号位mm；

p₂为盾壳单位面积上的摩擦力，单位符号为Pa；

盾壳表面任一微单元的坐标为：

(-lcosβ-Rsinθsinβ，-Rcosθ，h+lsinβ-Rsinθcosβ)

经过坐标变换，得到用于代入Mindlin位移解的等效坐标：x₂＝x+lcosβ+Rsinθsinβ；y₂＝y+Rcosθ；h₂＝h+lsinβ-Rsinθcosβ；

则盾壳表面任一微单元荷载作用点、及其关于地面的对称点，到土体沉降计算点之间的距离分别为：

$M_2=\sqrt{{x_2}^2+{y_2}^2+{(z-h_2)}^2}$

$N_2=\sqrt{{x_2}^2+{y_2}^2+{(z+h_2)}^2}$

将dp₂分解为水平分力dp_2h＝p₂cosβRdldθ和竖向分力dp_2v＝p₂sinβRdldθ，分别代入Mindlin水平和竖向位移解，分别进行积分计算；

得到在盾壳摩擦力的水平分力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

$w_{2h}=\frac{p_{2}Rcos\mathrm{\β}}{16\mathrm{\π}G(1-\mathrm{\μ})}{\∫}_0^{2\mathrm{\π}}{\∫}_0^L{x}_2\[\frac{z-h_2}{M_2^3}+\frac{(3-4\mathrm{\μ})(z-h_2)}{N_2^3}-\frac{6{\mathrm{zh}}_2(z+h_2)}{N_2^5}+\frac{4(1-\mathrm{\μ})(1-2\mathrm{\μ})}{N_2(N_2+z+h_2)}\]dld\mathrm{\θ}$

式中：

L为盾构长度，单位符号为mm；

同时，盾构机盾壳摩擦力的竖向分力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

$w_{2v}=\frac{p_{2}R\sin \mathrm{\β}}{16\mathrm{\π}G(1-\mathrm{\μ})}{\∫}_0^{2\mathrm{\π}}{\∫}_0^L\[\frac{(3-4\mathrm{\μ})}{M_2}+\frac{8{(1-\mathrm{\μ})}^2-(3-4\mathrm{\μ})}{N_2}+\frac{{(z-h_2)}^2}{M_2^3}+\frac{(3-4\mathrm{\μ}){(z+h_2)}^2-2h_{2}z}{N_2^3}+\frac{6h_{2}z{(z+h_2)}^2}{N_2^5}\]dld\mathrm{\θ}$

在盾构机盾壳摩擦力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

w₂＝w_2h+w_2v

步骤3)、附加注浆压力引起的土体垂直变形计算：

将盾尾注浆力看作一种环向力反作用于周围的土体；取盾构的盾尾单元dA＝Rdldθ，其所受的集中力为：

dp₃＝p₃Rdldθ

式中：

p₃为盾尾附加注浆压力，单位符号为Pa；

该盾尾单元的坐标表示为：

(-Lcosβ-lcosβ-Rsinθsinβ，-Rcosθ，h+Lsinβ+lsinβ-Rsinθcosβ)；

经过坐标变换，得到用于代入Mindlin位移解的等效坐标：x₃＝x+Lcosβ+lcosβ+Rsinθsinβ；y₃＝y+Rcosθ；h₃＝h+Lsinβ+lsinβ-Rsinθcosβ；

则盾尾任一微单元荷载作用点、及其关于地面的对称点，到土体沉降计算点之间的距离分别为：

$M_3=\sqrt{{x_3}^2+{y_3}^2+{(z-h_3)}^2}$

$N_3=\sqrt{{x_3}^2+{y_3}^2+{(z+h_3)}^2}$

将dp₃分解为分别与x、y、z轴平行的力dp_3x＝-p₃sinθsinβRdθdl、dp_3y＝-p₃cosθRdθd、dp_3z＝-p₃sinθcosβRdθdl，再分别代入Mindlin水平和竖向位移解，分别进行积分计算；

得到在盾尾附加注浆压力的x方向分力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

$w_{3x}=\frac{-p_{3}R\sin \mathrm{\β}}{16\mathrm{\π}G(1-\mathrm{\μ})}{\∫}_0^b{\∫}_0^{2\mathrm{\π}}{\mathrm{sin\θx}}_3\[\frac{z-h_3}{M_3^3}+\frac{(3-4\mathrm{\μ})(z-h_3)}{N_3^3}-\frac{6{\mathrm{zh}}_3(z+h_3)}{N_3^5}+\frac{4(1-\mathrm{\μ})(1-2\mathrm{\μ})}{N_3(N_3+z+h_3)}\]d\mathrm{\θ}dl$

式中：

b为盾尾注浆长度，单位符号为mm；

在盾尾附加注浆压力的y方向分力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

$w_{3y}=\frac{-p_{3}R}{16\mathrm{\π}G(1-\mathrm{\μ})}{\∫}_0^b{\∫}_0^{2\mathrm{\π}}{\mathrm{cos\θy}}_3\[\frac{z-h_3}{M_3^3}+\frac{(3-4\mathrm{\μ})(z-h_3)}{N_3^3}-\frac{6{\mathrm{zh}}_3(z+h_3)}{N_3^5}+\frac{4(1-\mathrm{\μ})(1-2\mathrm{\μ})}{N_3(N_3+z+h_3)}\]d\mathrm{\θ}dl$

在盾尾附加注浆压力的z方向分力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

$w_{3z}=\frac{-p_{3}Rcos\mathrm{\β}}{16\mathrm{\π}G(1-\mathrm{\μ})}{\∫}_0^b{\∫}_0^{2\mathrm{\π}}\sin \mathrm{\θ}\[\frac{(3-4\mathrm{\μ})}{M_3}+\frac{8{(1-\mathrm{\μ})}^2-(3-4\mathrm{\μ})}{N_3}+\frac{{(z-h_3)}^2}{M_3^3}+\frac{(3-4\mathrm{\μ}){(z+h_3)}^2-2h_{3}z}{N_3^3}+\frac{6h_{3}z{(z+h_3)}^2}{N_3^5}\]d\mathrm{\θ}dl$

在盾尾附加注浆压力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

w₃＝w_3x+w_3y+w_3z

步骤4)、土体损失引起的土体垂直变形计算：

将地面出入式盾构隧道，简化成沿隧道掘进方向埋深线性变化的隧道，盾构轴线埋深公式：

h(x)＝h-xtanβ

将上述公式作为隧道轴线埋深，代入统一土体移动模型三维解，得到土体损失引起的土体垂直变形计算公式：

$w_4=\frac{{\mathrm{B\ηR}}^2}{4}\{\frac{h\left(x\right)-z}{y^2+{\left(h\right(x)-z)}^2}+\frac{h\left(x\right)+z}{y^2+{\left(h\right(x)+z)}^2}-\frac{2z\[y^2-{\left(h\right(x)+z)}^2\]}{{\[y^2+{\left(h\right(x)+z)}^2\]}^2}\}\[1-\frac{x}{\sqrt{x^2+h{\left(x\right)}^2}}\]\exp \[\frac{y^2\ln \mathrm{\λ}}{{\left(h\right(x)+R)}^2}+\frac{z^2(\ln \mathrm{\λ}-\ln \mathrm{\δ})}{{\left(h\right(x)+d)}^2}\]$

式中：

η为最大土体损失率；

沿盾构掘进方向x距离处的土体损失率η(x)为：

$\mathrm{\η}\left(x\right)=\frac{\mathrm{\η}}{2}\[1-\frac{x}{\sqrt{x^2+h{\left(x\right)}^2}}\];$

另外式中：

$B=\frac{4h\left(x\right)\[h\left(x\right)+d-\sqrt{{\left(h\right(x)+d)}^2-\mathrm{\η}\left(x\right){(R+d)}^2}\]}{R\mathrm{\η}\left(x\right)(R+d)};$

$\mathrm{\λ}=\frac{1}{4}-\frac{g\left(x\right)}{\mathrm{\π}R\mathrm{\η}\left(x\right)}\[\arcsin \left(\frac{d}{R-g\left(x\right)/2}\right)+\sqrt{1-{\left(\frac{d}{R-g\left(x\right)/2}\right)}^2}-1\];$

$\mathrm{\δ}=\frac{1}{2}-\frac{g\left(x\right)}{{\mathrm{\πR}}^2\mathrm{\η}\left(x\right)}(R-\frac{g\left(x\right)}{4})\arcsin \left(\frac{d}{R-g\left(x\right)/4}\right);$

d为土体移动焦点到盾构中心的距离，单位符号为mm；

隧道沿掘进方向x距离处的等效土体损失参数g(x)为：

在施工前根据具体的现场施工参数，如掘削面单位面积上的正面附加推力p₁、开挖面处盾构轴线埋深h、盾构机外直径D、土的泊松比μ、土的剪切弹性模量G、土的压缩模量E_s、静止土压力系数K₀、盾构半径R、盾壳单位面积上的摩擦力p₂、盾构长度L、盾尾附加注浆压力p₃、盾尾注浆长度b、最大土体损失率η，模拟不同参数的施工条件下，所能够产生的土体中任一位置土体垂直变形大小；若地表沉降超过相应允许值，则需调整上述相关施工参数并进行试算，直至土体垂直变形低于或者等于相应允许值，从而使得施工达到安全标准。

本发明的有益效果如下：

本专利深入研究了地面出入式盾构施工中，掘削面正面附加推力、盾壳摩擦力、盾尾附加注浆压力以及土体沉降引起的土体垂直位移规律，通过推导出的公式可计算实际工程中，地面出入式盾构引起的土体垂直位移大小。

施工前可根据具体的现场施工参数，如掘削面单位面积上的正面附加推力p₁、开挖面处盾构轴线埋深h、盾构机外直径D、土的泊松比μ、土的剪切弹性模量G、土的压缩模量E_s、静止土压力系数K₀、盾构半径R、盾壳单位面积上的摩擦力p₂、盾构长度L、盾尾附加注浆压力p₃、盾尾注浆长度b、最大土体损失率η，模拟不同参数的施工条件下，可能产生的地表沉降值大小。

在实际情况中，工程施工对地表沉降大小有严格控制，若地表沉降超过相应允许值，则存在工程安全隐患，甚至造成地表塌陷、周边建筑物倾斜、地下管线破坏等严重后果。

因此施工前可通过本专利的公式对具体工程的施工进行模拟，计算出指定工况下的地表沉降大小，若地表沉降超过相应允许值，可调整相关施工参数进行试算，直至达到安全标准。

本专利通过理论公式，对实际地面出入式盾构施工中的地表沉降大小进行预测，对工程具有预防、指导作用，并且为今后有关地面出入式盾构施工对周围环境影响方面的研究提供了理论基础。

附图说明

图1为本发明所采用方法与林存刚^[1]方法的对比示意图。

图2为本发明所采用方法的计算模型示意图。

图3为本发明中诸多因素引起的纵向地面垂直变形曲线示意图。

图4为本发明中不同β时的纵向地面垂直变形曲线示意图。

具体实施方式

下面结合说明书附图对本发明的技术方案作进一步说明：

如图1～4所示，本发明提供一种地面出入式盾构法隧道施工引起的土体垂直变形计算方法，由于本发明真实考虑到盾构推进方向和掘削面正面附加推力、盾壳摩擦力、盾尾附加注浆压力均与水平面有一定夹角β(见图1b，以向上为正，向下为负)。分别提出掘削面正面附加推力、盾壳摩擦力、盾尾附加注浆压力以及土体损失各因素引起的土体垂直变形计算公式。

本发明所采用方法的力学计算模型见图2。

图中x为离开挖面的水平距离，单位符号为mm，以掘进方向为正；

y为离盾构轴线的横向水平距离，单位符号为mm；

z为盾构轴线离地面的竖向距离，单位符号为mm，以向下为正。

本专利方法具体包括如下步骤：

步骤1)、正面附加推力引起的土体垂直变形计算：

取盾构开挖面内任一微单元dA＝rdrdθ，其所受的集中力为：

dp₁＝p₁rdrdθ，

式中：

A、r、θ分别为微单元面积、半径、角度，符号单位分别为mm²、mm、°；

p₁为掘削面单位面积上的正面附加推力，单位符号为Pa；

开挖面内任一微单元坐标为：

(-rsinθsinβ，-rcosθ，h-rsinθcosβ)，

式中：

h为开挖面处盾构轴线埋深，单位符号为mm；

经过坐标变换，得到用于代入Mindlin位移解的等效坐标：x₁＝x+rsinθsinβ；y₁＝y+rcosθ；h₁＝h-rsinθcosβ；

设盾构开挖面任一微单元荷载作用点、及其关于地面的对称点，到土体沉降计算点之间的距离分别为：

$M_1=\sqrt{{x_1}^2+{y_1}^2+{(z-h_1)}^2},$

$N_1=\sqrt{{x_1}^2+{y_1}^2+{(z+h_1)}^2},$

将dp₁分解为水平力dp_1h＝p₁cosβrdrdθ和竖向力dp_1v＝p₁sinβrdrdθ，分别代入Mindlin水平和竖向位移解进行积分计算；

得到在掘削面正面附加推力的水平分力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

$w_{1h}=\frac{p_{1}cos\mathrm{\β}}{16\mathrm{\π}G(1-\mathrm{\μ})}{\∫}_0^{2\mathrm{\π}}{\∫}_0^{D/2}{x}_1\[\frac{z-h_1}{M_1^3}+\frac{(3-4\mathrm{\μ})(z-h_1)}{N_1^3}-\frac{6{\mathrm{zh}}_1(z+h_1)}{N_1^5}+\frac{4(1-\mathrm{\μ})(1-2\mathrm{\μ})}{N_1(N_1+z+h_1)}\]rdrd\mathrm{\θ},$

式中：

D为盾构机外直径，单位符号为mm；

μ为土的泊松比；

G为土的剪切弹性模量，单位符号为Pa，

E_s为土的压缩模量，单位符号为Pa；

K₀为静止土压力系数；

π为圆周率，一般取3.14；

同时，在盾构掘削面正面附加推力的竖向分力作用下，土体中任一点(x，y，z)处产生的土体垂直变形为：

$w_{1v}=\frac{p_1\sin \mathrm{\β}}{16\mathrm{\π}G(1-\mathrm{\μ})}{\∫}_0^{2\mathrm{\π}}{\∫}_0^{D/2}\[\frac{(3-4\mathrm{\μ})}{M_1}+\frac{8{(1-\mathrm{\μ})}^2-(3-4\mathrm{\μ})}{N_1}+\frac{{(z-h_1)}^2}{M_1^3}+\frac{(3-4\mathrm{\μ}){(z+h_1)}^2-2h_{1}z}{N_1^3}+\frac{6h_{1}z{(z+h_1)}^2}{N_1^5}\]rdrd\mathrm{\θ}$

因此，在盾构掘削面正面附加推力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

w₁＝w_1h+w_1v

步骤2)、盾壳摩擦力引起的土体垂直变形计算：

由于盾构机为一圆柱体，取盾壳表面任一微单元dA＝Rdldθ，其所受的摩擦力为：

dp₂＝p₂Rdldθ

式中：

R为盾构半径，单位符号为mm；

l为微单元长度，单位符号位mm；

p₂为盾壳单位面积上的摩擦力，单位符号为Pa；

盾壳表面任一微单元的坐标为：

(-lcosβ-Rsinθsinβ，-Rcosθ，h+lsinβ-Rsinθcosβ)

经过坐标变换，得到用于代入Mindlin位移解的等效坐标：x₂＝x+lcosβ+Rsinθsinβ；y₂＝y+Rcosθ；h₂＝h+lsinβ-Rsinθcosβ；

则盾壳表面任一微单元荷载作用点、及其关于地面的对称点，到土体沉降计算点之间的距离分别为：

$M_2=\sqrt{{x_2}^2+{y_2}^2+{(z-h_2)}^2}$

$N_2=\sqrt{{x_2}^2+{y_2}^2+{(z+h_2)}^2}$

将dp₂分解为水平分力dp_2h＝p₂cosβRdldθ和竖向分力dp_2v＝p₂sinβRdldθ，分别代入Mindlin水平和竖向位移解，分别进行积分计算；

得到在盾壳摩擦力的水平分力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

$w_{2h}=\frac{p_{2}Rcos\mathrm{\β}}{16\mathrm{\π}G(1-\mathrm{\μ})}{\∫}_0^{2\mathrm{\π}}{\∫}_0^L{x}_2\[\frac{z-h_2}{M_2^3}+\frac{(3-4\mathrm{\μ})(z-h_2)}{N_2^3}-\frac{6{\mathrm{zh}}_2(z+h_2)}{N_2^5}+\frac{4(1-\mathrm{\μ})(1-2\mathrm{\μ})}{N_2(N_2+z+h_2)}\]dld\mathrm{\θ}$

式中：

L为盾构长度，单位符号为mm；

同时，在盾壳摩擦力的竖向分力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

$w_{2v}=\frac{p_{2}R\sin \mathrm{\β}}{16\mathrm{\π}G(1-\mathrm{\μ})}{\∫}_0^{2\mathrm{\π}}{\∫}_0^L\[\frac{(3-4\mathrm{\μ})}{M_2}+\frac{8{(1-\mathrm{\μ})}^2-(3-4\mathrm{\μ})}{N_2}+\frac{{(z-h_2)}^2}{M_2^3}+\frac{(3-4\mathrm{\μ}){(z+h_2)}^2-2h_{2}z}{N_2^3}+\frac{6h_{2}z{(z+h_2)}^2}{N_2^5}\]dld\mathrm{\θ}$

在盾壳摩擦力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

w₂＝w_2h+w_2v

步骤3)、附加注浆压力引起的土体垂直变形计算：

将盾尾注浆力看作一种环向力反作用于周围的土体；取盾构的盾尾单元dA＝Rdldθ，其所受的集中力为：

dp₃＝p₃Rdldθ

式中：

p₃为盾尾附加注浆压力，单位符号为Pa；

该盾尾单元的坐标表示为：

(-Lcosβ-lcosβ-Rsinθsinβ，-Rcosθ，h+Lsinβ+lsinβ-Rsinθcosβ)；

经过坐标变换，得到用于代入Mindlin位移解的等效坐标：x₃＝x+Lcosβ+lcosβ+Rsinθsinβ；y₃＝y+Rcosθ；h₃＝h+Lsinβ+lsinβ-Rsinθcosβ；

则盾尾任一微单元荷载作用点、及其关于地面的对称点，到土体沉降计算点之间的距离分别为：

$M_3=\sqrt{{x_3}^2+{y_3}^2+{(z-h_3)}^2}$

$N_3=\sqrt{{x_3}^2+{y_3}^2+{(z+h_3)}^2}$

将dp₃分解为分别与x、y、z轴平行的力dp_3x＝-p₃sinθsinβRdθdl、dp_3y＝-p₃cosθRdθdl、dp_3z＝-p₃sinθcosβRdθdl，再分别代入Mindlin水平和竖向位移解，分别进行积分计算；

得到在盾尾附加注浆压力的x方向分力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

$w_{3x}=\frac{-p_{3}R\sin \mathrm{\β}}{16\mathrm{\π}G(1-\mathrm{\μ})}{\∫}_0^b{\∫}_0^{2\mathrm{\π}}{\mathrm{sin\θx}}_3\[\frac{z-h_3}{M_3^3}+\frac{(3-4\mathrm{\μ})(z-h_3)}{N_3^3}-\frac{6{\mathrm{zh}}_3(z+h_3)}{N_3^5}+\frac{4(1-\mathrm{\μ})(1-2\mathrm{\μ})}{N_3(N_3+z+h_3)}\]d\mathrm{\θ}dl$

式中：

b为盾尾注浆长度，单位符号为mm；

在盾尾附加注浆压力的y方向分力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

$w_{3y}=\frac{-p_{3}R}{16\mathrm{\π}G(1-\mathrm{\μ})}{\∫}_0^b{\∫}_0^{2\mathrm{\π}}{\mathrm{cos\θy}}_3\[\frac{z-h_3}{M_3^3}+\frac{(3-4\mathrm{\μ})(z-h_3)}{N_3^3}-\frac{6{\mathrm{zh}}_3(z+h_3)}{N_3^5}+\frac{4(1-\mathrm{\μ})(1-2\mathrm{\μ})}{N_3(N_3+z+h_3)}\]d\mathrm{\θ}dl$

在盾尾附加注浆压力的z方向分力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

$w_{3z}=\frac{-p_{3}Rcos\mathrm{\β}}{16\mathrm{\π}G(1-\mathrm{\μ})}{\∫}_0^b{\∫}_0^{2\mathrm{\π}}\sin \mathrm{\θ}\[\frac{(3-4\mathrm{\μ})}{M_3}+\frac{8{(1-\mathrm{\μ})}^2-(3-4\mathrm{\μ})}{N_3}+\frac{{(z-h_3)}^2}{M_3^3}+\frac{(3-4\mathrm{\μ}){(z+h_3)}^2-2h_{3}z}{N_3^3}+\frac{6h_{3}z{(z+h_3)}^2}{N_3^5}\]d\mathrm{\θ}dl$

在盾尾附加注浆压力作用下，土体中任一点(x，y，z)处产生的垂直变形为：

w₃＝w_3x+w_3y+w_3z

步骤4)、土体损失引起的土体垂直变形计算：

将地面出入式盾构隧道，简化成沿隧道掘进方向埋深线性变化的隧道，盾构轴线埋深公式：

h(x)＝h-xtanβ

将上述公式作为隧道轴线埋深，代入统一土体移动模型三维解，得到土体损失引起的土体垂直变形计算公式：

$w_4=\frac{{\mathrm{B\ηR}}^2}{4}\{\frac{h\left(x\right)-z}{y^2+{\left(h\right(x)-z)}^2}+\frac{h\left(x\right)+z}{y^2+{\left(h\right(x)+z)}^2}-\frac{2z\[y^2-{\left(h\right(x)+z)}^2\]}{{\[y^2+{\left(h\right(x)+z)}^2\]}^2}\}\[1-\frac{x}{\sqrt{x^2+h{\left(x\right)}^2}}\]\exp \[\frac{y^2\ln \mathrm{\λ}}{{\left(h\right(x)+R)}^2}+\frac{z^2(\ln \mathrm{\λ}-\ln \mathrm{\δ})}{{\left(h\right(x)+d)}^2}\]$

式中：

η为最大土体损失率；

沿盾构掘进方向x距离处的土体损失率η(x)为：

$\mathrm{\η}\left(x\right)=\frac{\mathrm{\η}}{2}\[1-\frac{x}{\sqrt{x^2+h{\left(x\right)}^2}}\];$

另外式中：

$B=\frac{4h\left(x\right)\[h\left(x\right)+d-\sqrt{{\left(h\right(x)+d)}^2-\mathrm{\η}\left(x\right){(R+d)}^2}\]}{R\mathrm{\η}\left(x\right)(R+d)};$

$\mathrm{\λ}=\frac{1}{4}-\frac{g\left(x\right)}{\mathrm{\π}R\mathrm{\η}\left(x\right)}\[\arcsin \left(\frac{d}{R-g\left(x\right)/2}\right)+\sqrt{1-{\left(\frac{d}{R-g\left(x\right)/2}\right)}^2}-1\];$

$\mathrm{\δ}=\frac{1}{2}-\frac{g\left(x\right)}{{\mathrm{\πR}}^2\mathrm{\η}\left(x\right)}(R-\frac{g\left(x\right)}{4})\arcsin \left(\frac{d}{R-g\left(x\right)/4}\right);$

d为土体移动焦点到盾构中心的距离，单位符号为mm；

隧道沿掘进方向x距离处的等效土体损失参数g(x)为：

在施工前根据具体的现场施工参数，例如掘削面单位面积上的正面附加推力p₁、开挖面处盾构轴线埋深h、盾构机外直径D、土的泊松比μ、土的剪切弹性模量G、土的压缩模量E_s、静止土压力系数K₀、盾构半径R、盾壳单位面积上的摩擦力p₂、盾构长度L、盾尾附加注浆压力p₃、盾尾注浆长度b、最大土体损失率η，模拟不同参数的施工条件下，所能够产生的土体中任一位置土体垂直变形大小；若地表沉降超过相应允许值，则需调整上述相关施工参数并进行试算，直至土体垂直变形低于或者等于相应允许值，从而使得施工达到安全标准。

本专利深入研究了地面出入式盾构施工中，掘削面正面附加推力、盾壳摩擦力、盾尾附加注浆压力以及土体沉降引起的土体垂直位移规律，通过推导出的公式可计算实际工程中，地面出入式盾构引起的土体垂直位移大小。

施工前可根据具体的现场施工参数，如掘削面单位面积上的正面附加推力p₁、开挖面处盾构轴线埋深h、盾构机外直径D、土的泊松比μ、土的剪切弹性模量G、土的压缩模量E_s、静止土压力系数K₀、盾构半径R、盾壳单位面积上的摩擦力p₂、盾构长度L、盾尾附加注浆压力p₃、盾尾注浆长度b、最大土体损失率η，模拟不同参数的施工条件下，可能产生的地表沉降值大小。

在实际情况中，工程施工对地表沉降大小有严格控制，若地表沉降超过相应允许值，则存在工程安全隐患，甚至造成地表塌陷、周边建筑物倾斜、地下管线破坏等严重后果。

因此施工前可通过本专利的公式对具体工程的施工进行模拟，计算出指定工况下的地表沉降大小，若地表沉降超过相应允许值，可调整相关施工参数进行试算，直至达到安全标准。

本专利通过理论公式，对实际地面出入式盾构施工中的地表沉降大小进行预测，对工程具有预防、指导作用，并且为今后有关地面出入式盾构施工对周围环境影响方面的研究提供了理论基础。

另外：Mindlin水平位移解：

$w=\frac{Px}{16\mathrm{\π}G(1-\mathrm{\μ})}\[\frac{z-c}{M^3}+\frac{(3-4\mathrm{\μ})(z-c)}{N^3}-\frac{6cz(z+c)}{N^5}+\frac{4(1-\mathrm{\μ})(1-2\mathrm{\μ})}{N(N+z+c)}\]$

式中：w为土体位移，单位符号为mm；

P为作用在c深度处的水平集中力，单位符号为N；

c为距地表的距离，单位符号为mm；

M为荷载作用点作用点到土体沉降计算点之间的距离，单位符号为mm；

N荷载作用点关于地面的对称点到土体沉降计算点之间的距离，单位符号为mm。

Mindlin竖向位移解：

$w=\frac{P}{16\mathrm{\π}G(1-\mathrm{\μ})}\[\frac{(3-4\mathrm{\μ})}{M}+\frac{8{(1-\mathrm{\μ})}^2-(3-4\mathrm{\μ})}{N}+\frac{{(z-c)}^2}{M^3}+\frac{(3-4\mathrm{\μ}){(z+c)}^2-2cz}{N^3}+\frac{6cz{(z+c)}^2}{N^5}\]$

统一土体移动模型三维解：

$w=\frac{{\mathrm{B\ηR}}^2}{4}\{\frac{h-z}{y^2+{(h-z)}^2}+\frac{h+z}{y^2+{(h+z)}^2}-\frac{2z\[y^2-{(h+z)}^2\]}{{\[y^2+{(h+z)}^2\]}^2}\}(1-\frac{x}{\sqrt{x^2+h^2}})\exp \[\frac{y^2\ln \mathrm{\λ}}{{(h+R)}^2}+\frac{z^2(\ln \mathrm{\λ}-\ln \mathrm{\δ})}{{(h+d)}^2}\]$

具体地：将本专利以南京机场线秣陵站～将军路站区间的地面出入段工程^[2]为背景，采用单线地面出入式盾构法施工。

图3为当β＝1.6°时，各种施工因素引起的轴线上方纵向地面垂直变形计算结果。如图所示：(1)土体损失是引起地面垂直变形的主要因素，开挖面前方地面沉降较小，后方沉降较大。由于注浆压力作用，在开挖面后方约12m处，地面沉降相对较小，曲线出现局部凸起；(2)正面附加推力引起开挖面前方地面隆起，后方地面沉降，以盾构开挖面为轴线呈反对称分布，本算例中正面附加推力引起的最大地面隆起为0.5mm，出现在开挖面前方大约2m处；(3)盾壳摩擦力引起的地面变形规律与正面附加推力相似，但引起的地面变形较大，以盾构机中部为轴线呈反对称分布。本算例中盾壳摩擦力引起的最大地面隆起为3.4mm，出现在开挖面前方约2m处；(4)附加注浆压力引起的地面隆起形状类似于正态分布，本算例中附加注浆压力产生的最大隆起值为4.7mm，出现在开挖面后方约12m处。

图4为β分别取0°、1°、3°、5°、7°时，总的纵向地面垂直变形计算结果。如图所示：(1)盾构上仰掘进时，引起的总地面沉降均比常规盾构(β＝0°)小；(2)随着β增大，总的地面垂直变形曲线呈上移趋势。当β＝7°时，开挖面前方4m左右处地面由沉降变为隆起，沿隧道纵向开挖面前方10m左右处隆起最大，约为0.7mm。开挖面后方60m处地面沉降值比常规盾构小8mm左右。

上述实施例是对本发明的说明，不是对本发明的限定，任何对本发明简单变换后的方案均属于本发明的保护范围。

其中：对本发明中所涉及的一些引用文献做如下简单说明：

[1]林存刚，刘干斌，梁荣柱，等.隧道坡度对盾构掘进引起地面隆陷的影响[J].岩土工程学

报，2014，36(7)：1203-1212.

LIN Cun-gang，LIU Gan-bin，LIANG Rong-zhu，et al.Influences of tunnel slope on shield tunnelling-induced heave and subsidence of ground surface[J].Chinese Journal of Geotechnical Engineering，2014，36(7)：1203-1212.

[2]吴惠明.地面出入式盾构隧道结构变形特性及控制研究[D].上海：上海大学，2014.

WU Hui-ming.Study on characteristic analyse and controlling technogy of structure deformation in GPST[D].Shanghai：Shanghai University，2014.